![]()

![]()
![]() 七年级数学下学期期末检测试题 (卷)
七年级数学下学期期末检测试题 (卷)
亲爱的同学,时间过得真快!在你即将告别七年级之际,这份数学试卷将为你提供展示才情和学识的舞台。只要你沉着、冷静,一定能展示出自己的最佳风采,好好地表现自己吧,为自己充满回忆的七年级学习生活画上最美、最亮的休止符!祝你考出好成绩!
| 题 号 | 一题 | 二题 | 三题 | 四题 | 总 分 | 评卷人 |
| 得 分 |
![]()
 一、耐心填一填(第9小题4分,其它小题每题2分,共20分)
一、耐心填一填(第9小题4分,其它小题每题2分,共20分)
1、等腰三角形的三边长分别为:x+1、 2x+3 、9 。则x= ;
2、在如图所示的五个方格中的字母都表示数字,中间一行的三个数字从左到右组成的三位数100d+10b+e恰好可以表示为![]() ,中间一列三个数字从上到下组成的三位数
,中间一列三个数字从上到下组成的三位数![]() (m、n都是正整数),则m+n=
;
(m、n都是正整数),则m+n=
;
3、若![]() 则
则![]() 。
。
4.把a4-16分解因式是 。
5.小亮解方程组 ![]() 的解为
的解为 ![]() ,由于不小心,滴上了两滴墨水, 刚好遮住了两个数●和★,请你帮他找回这两个数●= ,★= ;
,由于不小心,滴上了两滴墨水, 刚好遮住了两个数●和★,请你帮他找回这两个数●= ,★= ;
6.七⑴班学生42人去公园划船,共租用10艘船。 大船每艘可坐5人,小船每艘可坐3人,每艘船都坐满。问大船、小船各租了多少艘?设坐大船的有x人,坐小船的有y人,由题意可得方程组为: 。
7、观察下列各式: 1+1×3 = 22, 1+2×4 = 32, 1+3×5 = 42,……
请将你找出的规律用公式表示出来: .
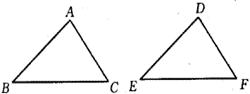 8,如右图,在△ABC和△DEF中,已知AB=DE,要使△ABC≌△DEF,根据三角形全等的判定定理,还需添加条件(填上你认为正确的两种情况)__________________ _____________________________________________.
8,如右图,在△ABC和△DEF中,已知AB=DE,要使△ABC≌△DEF,根据三角形全等的判定定理,还需添加条件(填上你认为正确的两种情况)__________________ _____________________________________________.
9.为了了解全市七年级学生的体重情况,从中抽查了500名学生。在这个问题中,总体是__________________________________;个体是___________________________________;样本是______________________________样本容量是____________。
![]() 二:精心选一选:(只有一个答案正确,每题3分,共36分)
二:精心选一选:(只有一个答案正确,每题3分,共36分)
1、如果![]() 是一个完全平方式,则m的值为 ( )
是一个完全平方式,则m的值为 ( )
A、3; B、6; C、±3; D、±6;
2、下列各式从左到右的变形中,属于因式分解的是 ( )
A、![]() ; B、
; B、![]() ;
;
C、![]() ;
D、
;
D、![]() ;
;
3.
对于二元一次方程![]() ,下列说法正确的是 ( )
,下列说法正确的是 ( )
A只有一个解; B共有两个解; C有无数个解; D任何一对有理数都是它的解
4.下列方程组中,是二元一次方程组的是 ( )
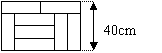 A、
A、![]() B、
B、![]() C、
C、![]() D、
D、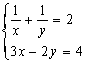
5.如上右图用8块相同的长方形地砖拼成一个大长方形,则每个长方形地砖的面积是( )
A、
6. 如果三角形的一个内角是其余两个内角的和,则这个三角形是 ( )
A.锐角三角形 B.直角三角形 C.等边三角形 D.钝角三角形
 7、下列三角形不全等的是 ( )
7、下列三角形不全等的是 ( )
A、 有两条边及其夹角对应相等的两个三角形
B、 有三个角对应相等的两个三角形
C、斜边和一个锐角对应相等的两个直角三角形
D、三条边对应相等的两个三角形
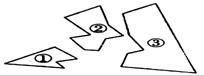
8、如右上图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的 玻璃,那么最省事的办法是 ( )
(A)带①去 (B)带②去 (C)带③去 (D)带①和②去
9.下列事件中,不确定事件是 ( )
A两直线平行,内错角相等; B拔苗助长;
C掷一枚硬币,国徽的一面朝上; D太阳每天早晨从东方升起。
10.下列调查最适合用抽样调查的是: ( )
A、要了解某大型水果批发市场水果的质量状况。 B、某单位要对职工进行体格检查。
C、语文老师在检查某个学生作文中的错别字。 D、学校要了解流感在本校的传染情况。
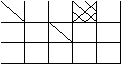
11、一只小狗在如图的方砖上走来走去,最终停在阴影方砖上的概率是 ( )
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
12、若一个事件不发生的机会是99.99%,那么这个事件 ( )
A.很可能发生 B.必然发生 C.不可能发生 D.不大可能发生
![]() 三、用心做一做(1至4题每题5分,第4、5、6三题每题8分,共44分)
三、用心做一做(1至4题每题5分,第4、5、6三题每题8分,共44分)
1![]() 2.
2.
![]()
3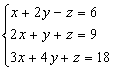 4、已知3x+y+2z=28,5x-3y+z=7,求x+y+z值。
4、已知3x+y+2z=28,5x-3y+z=7,求x+y+z值。
5.某市公园的门票价格如下表所示:
| 购票人数 | 1~50人 | 51~100人 | 100人以上 |
| 票价 | 10元/人 | 8元/人 | 5元/人 |
 某校初一年级甲乙两个班共100多人,去该公园举行联欢活动,其中甲班有50多人乙班不足50人,如果以班为单位买门票,一共要付920元;如果两个班一起买票,一共要付515元。甲、乙两班分别有多少人?(8分)
某校初一年级甲乙两个班共100多人,去该公园举行联欢活动,其中甲班有50多人乙班不足50人,如果以班为单位买门票,一共要付920元;如果两个班一起买票,一共要付515元。甲、乙两班分别有多少人?(8分)
![]() 6、如图,A、B两点分别位于一个池塘的两端,小明想用绳子测量A、B间的距离,但绳子不够长,你能帮他想个主意测量吗?(1)画出测量图案;(2)写出测量步骤;
6、如图,A、B两点分别位于一个池塘的两端,小明想用绳子测量A、B间的距离,但绳子不够长,你能帮他想个主意测量吗?(1)画出测量图案;(2)写出测量步骤;

|
|
7、我市某肉鸡场400只小鸡经过4个月饲养后的质量频数分布表如右图,其数据都不在分点上,
1)计算各组的频率,填在频数分布表中,并绘出频数分布直方图(附带折线图);(8分)
 2)质量在5.05千克
2)质量在5.05千克
| 组 别 | 频数 | 频率 |
| 4.55~5.05 | 40 |
|
| 5.05~5.55 | 80 |
|
| 5.55~6.05 | 160 |
|
| 6.05~6.55 | 80 |
|
| 6.55~7.05 | 30 |
|
| 7.05~7.55 | 10 |
|
以上的肉鸡属于合格
肉鸡产品,则产品合格
率是
3)质量在6.05千
克以上的肉鸡属于优
质肉鸡产品,则产品
优质率是
![]()
四、探索与创新,你尽心试一试,肯定能成功!(第1题4分,第二题6分,
每三题10分,共20分)
1、观察下面的点阵图和相应的等式,探究其中的规律:
(1)在④和⑤后面的横线上写出相应的等式;
④ .和⑤ .
(2)猜想写出与第n个点阵相对应的等式 .
![]()

 2. 解方程组
2. 解方程组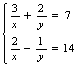 , 解:设
, 解:设![]() ,则原方程组可变形为关于m、n的
,则原方程组可变形为关于m、n的
方程组 。 解这个方程组得到它的解为 ,由
得原方程组的解为
由此可见,一个较为复杂的二元二次方程组,通过换元法可转化为简单的二元一次方程组。
3、如图,四边形ABCD中,AB=CD,AD=BC,AC与BD相交于O点,在图中:
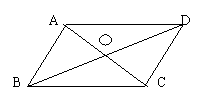 (1)由“SSS”可判定哪几对三角形全等,理由是
(1)由“SSS”可判定哪几对三角形全等,理由是
|
(2)由“ASA”或“AAS”可判定哪几对三角形全等,理由是
(3)求证:AB∥CD,AD∥BC, 且AC与BD的交点O平分四边形ABCD的对角线
AC与BD。

2004—2005学年度第二学期七年级数学
期末检测试题参考答案及评分标准
一、耐心填一填(第9小题4分,其它小题每题2分,共20分)
1、x= 3 ;
2、提示:若100d+10b+e=36=729,
3、 512 。
4.(a2+4)( a+2)( a-2)
5.●=8,★=-2;
6.
![]() x+y=42
x+y=42
![]() +
+![]() =10
=10
7、 1+n×(n+2) =(n+1)2
8,(1)AC=DF ,∠A=∠D; (2)∠A=∠D, ∠B=∠E; (3) ∠A=∠D,∠C=∠F;
(4) ∠B=∠E,∠C=∠F; (5)AC=DF ,BC=EF。以上答案只要给出任意2个均给满分。
9.总体是全市七年级学生的体重;个体是每个七年级学生的体重;样本是抽查的500名学生的体重;
样本容量是500。(此题每空1分)
二:精心选一选:(只有一个答案正确,每题3分,共36分)
1D;
2D; ![]() B;
12 D
B;
12 D
三、用心做一做(1至3题每题5分,第4题4分,5、6两题每题9分,第7题7分,共44分)
1. ![]() 解:两式相加得6x=66,x=11.(-----得2分)
解:两式相加得6x=66,x=11.(-----得2分)
两式相减得4y=28, y=7 (-----得2分)
原方程组的解是![]() (-----得1分)
(-----得1分)
2. ![]()
解:由x-3y=1,得x=3y+1,代入2x+y-15=1中后得7y=14,得y=2, (-----得3分)则x=7.(----得1分)
原方程组的解是![]() (-----得1分)
(-----得1分)
3. 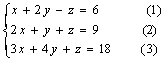
解:先消去未知数z,由(1)式+(2)式并化简得
x+y=5 (4) (----------得1分)
由(1)式+(3)式并化简得
2x+3y=12 (5) (----------得1分)
由(4)式和(5)式可求出 x=3, y=2, (----------得1分)
将之代入(1)式得z=1. (-----------得1分)
原方程组的解是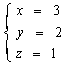 (-----得1分)
(-----得1分)
4、已知3x+y+2z=28,5x-3y+z=7,求x+y+z值.
解:增元求解。设x+y+z=k,把k当成已知数,可得三元一次方程组如下:
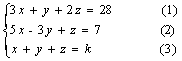
解:由(2)式-(3)式并化简得 4x-4y=7-k (4); (----------得2分)
由(1)式-(2)式×2并化简得-x+y=2 (5) (----------得2分)
由(4)式+(5)式×4并化简得 k=15 ,即 x+y+z=15 。 (----------得1分)
其它解法只要合理正确同样参照给分。
5、解:设甲、乙两班分别有x、y人。依题意得方程组:(----------得1分)

解这个方程组得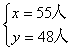 (----------得2分)
(----------得2分)
答:甲、乙两班分别有55人和48人。 (----------得1分)
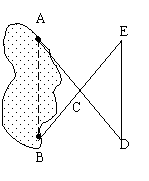
6、 解:(1)正确完成测量图的 (----------得2分)
(2)测量方法:在池塘边上找一点C,连接AC并处长至D,使AC=DC,同样连接BC并延长至E,使BC=EC,则DE=AB,量出DE的长度就是A、B间的距离。 (----------正确的得3分)
(3)理由:因为AC=DC,BC=EC,且∠ACB=∠DCE,所以
△ACB≌△DCE(SAS),AB=DE (----------正确的得3分)
7、1)正确填上频率表的 (----------得2分)
正确画出频数分布直方图的 (----------得3分)
正确画出折线图的 (----------得1分)
2)质量在5.05千克以上的肉鸡属于合格肉鸡产品,则产品合格率是90%(----------得1分)
3)质量在6.05千克以上的肉鸡属于优质肉鸡产品,则产品优质率是30%(----------得1分)
 |
| 组 别 | 频数 | 频率 |
| 4.55~5.05 | 40 | |
| 5.05~5.55 | 80 | |
| 5.55~6.05 | 160 | |
| 6.05~6.55 | 80 | |
| 6.55~7.05 | 30 | |
| 7.05~7.55 | 10 |
| 组 别 | 频数 | 频率 |
| 4.55~5.05 | 40 | 0.1 |
| 5.05~5.55 | 80 | 0.2 |
| 5.55~6.05 | 160 | 0.4 |
| 6.05~6.55 | 80 | 0.2 |
| 6.55~7.05 | 30 | 0.075 |
| 7.05~7.55 | 10 | 0.025 |
|
四、探索与创新,你尽心试一试,肯定能成功!(第1题4分,第二题6分,每三题10分,共20分)
1、1)④ 1+3+5+7=42 . (----------得1分)
⑤1+3+5+7+9=52 (----------得1分)
2)1+3+5+……+(2n-3)+(2n-1)=n2 . (----------得2分)
2. 解方程组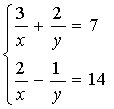 ,
,
解:设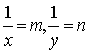 ,则原方程组可变形为关于m、n的方程组
,则原方程组可变形为关于m、n的方程组

解这个方程组得到它的解为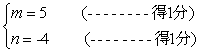 ,
,
由 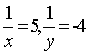 (----------得1分)
(----------得1分)
![]() 得原方程组的解为
得原方程组的解为 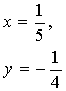 (---------得1分)
(---------得1分)
3、如图,四边形ABCD中,AB=CD,AD=BC,AC与BD相交于O点,在图中:
 1)由“SSS”可判定△ABD≌△CDB、△ABC≌△CDB这二对三角形全等, (--------------------------------得1分)
1)由“SSS”可判定△ABD≌△CDB、△ABC≌△CDB这二对三角形全等, (--------------------------------得1分)
理由是AB=CD,AD=BC,公共边BD=DB,则△ABD≌△CDB。同理AB=CD,AD=BC,公共边AC=CA,则△ABC≌△CDB。 (--------------得2分)
2)由“ASA”或“AAS”可判定△AOB≌△COD、△AOD≌△COB这二对三角形全等,
(-------------------------------------------------------------------得1分)
理由(1) 由△ABD≌△CDB可知∠ABO=∠CDO,由△ABC≌△CDB可知∠BAO=∠DCO,AB=CD,所以△AOB≌△COD (ASA) (------------------------------------得2分)
或(2) 由△ABD≌△CDB可知∠ABO=∠CDO,∠AOB=∠COD,AB=CD,所以△AOB≌△COD (AAS)同理可证△AOD≌△COB
3)求证:AB∥CD,AD∥BC, 且AC与BD的交点O平分四边形ABCD的对角线AC与BD。
由△ABD≌△CDB可知∠ABD=∠CDB,所以AB∥CD(内错角相等两直线平行),
同理可证AD∥BC。 (------------------------------------------------------得2分)
由△AOB≌△COD可知OA=OC,OB=OD, 所以AC与BD的交点O平分四边形ABCD的对角线AC与BD。(-------------------------------------------------------------------得2分)
答案证法不唯一 ,学生做答只要合理正确同样给分。