●方法点拨
［例1］计算
(1)(-3.5x2y2)·(0.6xy4z)
(2)(-ab3)2·(-a2b)
点拨：先确定运算顺序，再利用单项式乘单项式的法则进行计算.(1)直接作乘法即可，（2）先作乘方运算，再作乘法运算.
解：(1)(-3.5x2y2)·(0.6xy4z)
（系数相乘） （相同字母相乘） （不同字母相乘）（在x2·x中，x的指数是1，不要漏掉）
=-2.1x3y6z
(2)(-ab3)2·(-a2b)
=a2b6·(-a2b)——先算乘方
=-(a2·a2)(b6·b)——再算乘法
=-a4b7
［例2］计算
(1)am(am-a3+9)
(2)(4x3)2·［x3-x·(2x2-1)］
点拨：先确定运算顺序，再运用相应的公式进行计算.(2)中用到了幂的乘方，单乘多及去括号几种运算公式及方法，要一步步进行.
解：
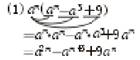
［例3］计算
(1)(2a+3b)(3a+2b) (2)(3m-n)2
点拨：这两题都需运用多项式相乘的法则进行计算，能合并同类项的要将结果化到最简的形式.注意第（2）题要化为多乘多的形式.
解：
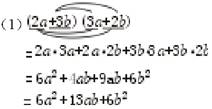
(2)(3m-n)2注意乘方的意义
=(3m-n)(3m-n)
=3m·3m-3m·n-n·3m+n·n
=9m2-3mn-3mn+n2
=9m2-6mn+n2
［例4］（1）(-
xy2)2·［xy(2x-y)+xy2］
(2)(-3x)2-2(x-5)(x-2)
点拨：对于混合运算，一定要注意运算顺序，尤其是乘方运算，每次运算后的结果要打上括号才能进行下一步运算.
解：(1)(- xy2)2·［xy(2x-y)+xy2］
=
x2y4·［2x2y-xy2+xy2］
=x2y4·(2x2y)
=
x4y5
(2)(-3x)2-2(x-5)(x-2)
=9x2-2(x2-2x-5x+10)
=9x2-2(x2-7x+10)
=9x2-2x2+14x-20
=7x2+14x-20
说明：一般来说，为了简化运算，能合并同类项的可先合并同类项，减少项数，再进行下一步的运算.
［例5］解下列方程
8x2-(2x-3)(4x+2)=14
点拨：利用多乘多法则将方程左边部分化简，再运用解方程的方法求出x.
解：8x2-(2x-3)(4x+2)=14
8x2-(8x2+4x-12x-6)=14
8x2-(8x2-8x-6)=14
8x2-8x2+8x+6=14
8x=8
x=1
［例6］长方形的一边长3m+2n,另一边比它大m-n,求长方形的面积.
点拨：先分别求出长和宽，再根据“长方形的面积=长×宽”求出面积.列式的时候，表示每条边的多项式都要用括号括起来.
解：长方形的宽：3m+2n
长方形的长=(3m+2n)+(m-n)=4m+n
长方形的面积：(3m+2n)·(4m+n)
=3m·4m+3m·n+2n·4m+2n·n
=12m2+3mn+8mn+2n2
=12m2+11mn+2n2
答：长方形的面积是12m2+11mn+2n2.