七年级数学相交线训练题

第五章相交线与平行线复习训练题

一、填空题

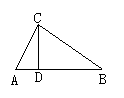
1、如图1,AC⊥BC,CD⊥AB, 垂足为D,图中共有___个直角,它们是__________________,图中线段_______的长表示点C到AB的距离，线段________的长表示点A到BC的距离.

2、如图2，直线a∥b，则∠ACB=_______。

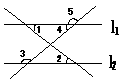
3、如图3，请你写出一个能判定l₁∥l₂的条件：　 _______.

(3)

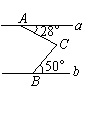
　　　(1)　　　　　　　　　  (2)

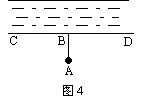
4、如图4，计划把河水引到水池A中，先引AB⊥CD，垂足为B，然后沿AB开渠，能使所开的渠道最短，这样设计的依据是_________________________________________。　

　　　　　 　 

　　 　　　　 (5)　　　　 　　　　　　　(6)　

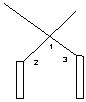
5、如图5，当剪子口∠AOB增大15°时，∠COD增大____________。　

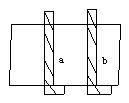
6、如图6两幢互相平行的大楼顶部各有一个射灯，当光柱相交时，∠1+ ∠2+∠3=___°

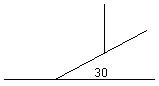
7、如图7有一个与地面成30°角的斜坡，，现要在斜坡上竖一电线杆，当电线杆与斜坡所成的角α=＿＿度角时，电线杆与地面垂直。

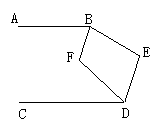
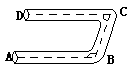
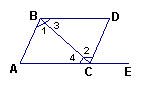
8、如图8，一个零件ABCD需要AB边与CD边平行，现只有一个量角器，测得拐角∠ABC=120°，∠BCD=60°这个零件合格吗？__________填（“合格”或“不合格”）

(7)　　　　　　　　　　  (8)　　　　　　　　　　  (9)

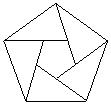
9、如图9是由五个同样的三角形组成的图案，三角形的三个角分别为36°、72°、72°，则图中共有＿＿＿ 对平行线。

10、如果一个角的两边与另一个角的两边分别垂直（或平行），那么这两个角的关系是_________。

二、选择题

1、一学员在广场上练习驾驶汽车，两次拐弯后，行驶的方向与原来的方向相同，这两次拐弯的角度可能是（　　 ）

 A、第一次向左拐30⁰，第二次向右拐30⁰ ;　

B、第一次向右拐50⁰，第二次向左拐130⁰;

C、第一次向右拐50⁰，第二次向右拐130⁰ ;　

D、第一次向左拐50⁰，第二次向左拐130⁰.

2、如图10，AB∥CD，那么∠A+∠C+∠AEC＝（　　）

A．360° 　 B．270°　 　 C．200°　  D．180°

　　　　  (10)　　　　　　　　　　 (11)　　　　　　　　　 (12)

3、在以下现象中:

①用打气筒打气时，气筒里活塞的运动；②传送带上，瓶装饮料的移动；

③在笔直的公路上行驶的汽车；④随风摆动的旗帜；⑤钟摆的摆动。属于平移的是（　）

（A）①　　（B）①②　　（C）①②③　　（D）①②③④

4、如图11所示，点在的延长线上，下列条件中能判断（　　）

 A. 　B. 　　 C. 　　D.

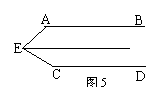
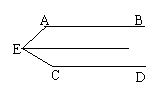
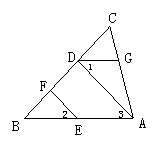
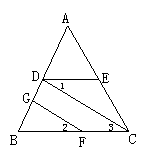
5、 如图12所示，平分，，图中相等的角共有（　　）

A. 3对　　　B. 4对　　  C. 5对　　　D. 6对

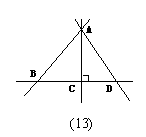
6、观察图形，下列说法正确的个数是（　　 ）

①过点A有且只有一条直线AC垂直于直线l；

②线段AC的长是点A到直线l的距离。

③线段AB、AC、AD中，线段AC最短，根据是垂线段最短；

④线段AB、AC、AD中，线段AC最短，根据是两点之间线段最短；　

A．1个　　B．2个　　 C．3个　 D．4个

7、下列说法中正确的是（　　　）　　　　　　　　　　　　　

A．三角形三条高所在的直线交于一点。B．有且只有一条直线与已知直线平行。

C．垂直于同一条直线的两条直线互相垂直。

D．从直线外一点到这条直线的垂线段，叫做这点到这条直线的距离。

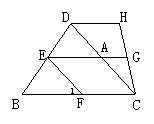
8、如图14，DH∥EG∥BC，且DC∥EF，那么图中和∠1相等的角的个数是（　 ）

A、2　　 B、4　　　C、5　　　D、6

　　　　　 

　　　　 (14)　　　　　　　　　　　　　　　　　  (15)

三、解答题

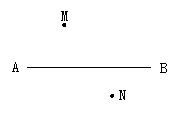
1、一辆汽车在直线形公路AB上由A向B行驶，M、N分别是位于AB两侧的村庄，设汽车行驶到公路AB上点P位置时，距离村庄M最近，行驶到公路AB上Q点时，距离村庄N最近，请在图15中标出点P、Q的位置（保留作图痕迹）

2、如图示，木工师傅用角尺画出工件边缘的两条垂线，这两条垂线平行吗？

为什么？

3、已知a、b、c是同一平面内的3条直线，给出下面6个命题：a∥b， b∥c，a∥c ，a⊥b，b⊥c，a⊥c，请从中选取3个命题（其中2个作为题设，1个作为结论）尽可能多地去组成一个真命题，并说出是运用了数学中的哪个道理。举例如下：

　 ∵a∥b， b∥c，∴a∥c（平行于同一条直线的两条直线平行）

4、（1）如图16，EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.

　　解： 因为EF∥AD，

　　　　 所以∠2=____ (_________________________________)

　　　　 又因为∠1=∠2

　　　　 所以∠1=∠3  (__________________)

　　　　 所以AB∥_____ (___________________________________)

　　　　 所以∠BAC+______=180°(___________________________)

　　　　 因为∠BAC=70°

　　　　 所以∠AGD=_______.

　　　　　  (16)　　　　　　　　　　　　　　　　　　　 (17)

（2）如图17，BD是∠ABC的平分线，ED∥BC，∠FED＝∠BDE,则EF也是

∠AED的平分线。完成下列推理过程：

∵　BD是∠ABC的平分线，（已知）

∴ ∠ABD=∠DBC(　　　　　　　　　　　　  )

∵　ED∥BC(已知)

∴ ∠BDE=∠DBC(　　　　　　　　　　　　　　　　 )

∴ ∠ABD=∠BDE(等量代换)，又∵∠FED=∠BDE（已知）

∴ EF∥BD(　　　　　　　　　　　　　　　　　　 )，

∴ ∠AEF=∠ABD(　　　　　　　　　　　　　　　 )

∴ ∠AEF=∠FED(　　　　　　　　  ),

所以EF是∠AED的平分线（角平分线的定义）

5、如图1，MA₁∥NA₂，则∠A₁＋∠A₂＝______________________度。

　 如图2，MA₁∥NA₃，则∠A₁＋∠A₂＋∠A₃＝________________________度。

　 如图3，MA₁∥NA₄，则∠A₁＋∠A₂＋∠A₃＋∠A₄＝_____________________度。

　 如图4，MA₁∥NA₅，则∠A₁＋∠A₂＋∠A₃＋∠A₄＋∠A₅＝________________度。

　 从上述结论中你发现了什么规律？

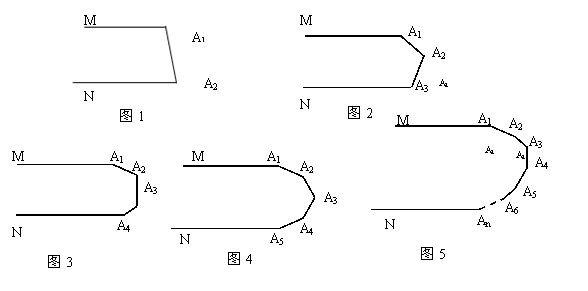　 如图5，MA₁∥NA_n，则∠A₁＋∠A₂＋∠A₃＋……＋∠A_n＝_________________度。

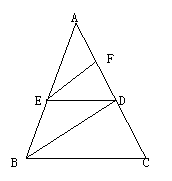
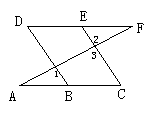
6、如图，若∠1=∠2,∠C=∠D,问∠A与∠F有什么关系?并说明理由.

7、如图,若∠DEC+∠ACB=180°,∠1=∠2,CD⊥AB,试问FG与AB垂直吗?说明理由.

8、如图，已知AB∥CD，∠ABE和∠CDE的平分线相交于F，∠E = 140º，求∠BFD的度数.