基础过关作业
1．以下说法错误的是（ ）
A．三角形的三条高一定在三角形内部交于一点
B．三角形的三条中线一定在三角形内部交于一点
C．三角形的三条角平分线一定在三角形内部交于一点
D．三角形的三条高可能相交于外部一点
2．如果一个三角形的三条高的交点恰好是这个三角形的一个顶点，那么这个三角形是（ ）
A．锐角三角形 B．直角三角形 C．钝角三角形 D．不能确定
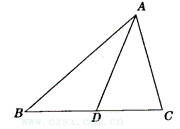
3．如图1，BD=
BC，则BC边上的中线为______，△ABD的面积=_____的面积．
(1) (2) (3)
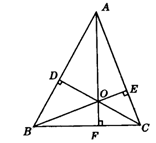
4．如图2，△ABC中，高CD、BE、AF相交于点O，则△BOC的三条高分别为线段________．
5．下列图形中具有稳定性的是（ ）
A．梯形 B．菱形 C．三角形 D．正方形
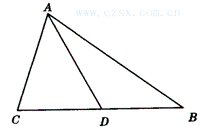
6．如图3，AD是△ABC的边BC上的中线，已知AB=
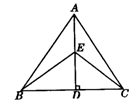
7．如图，∠BAD=∠CAD，AD⊥BC，垂足为点D，且BD=CD．可知哪些线段是哪个三角形的角平分线、中线或高？
综合创新作业
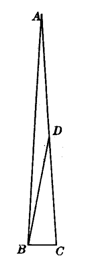
8．（综合题）如图5，在等腰三角形ABC中，AB=AC，一腰上的中线BD将这个等腰三角形的周长分为15和6两部分，求该等腰三角形的腰长及底边长．
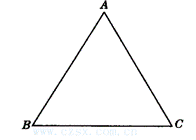
9．有一块三角形优良品种试验基地，如图所示，由于引进四个优良品种进行对比试验，需将这块土地分成面积相等的四块，请你制定出两种以上的划分方案供选择（画图说明）．
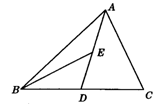
10．（创新题）如图，在△ABC中，D、E分别是BC、AD的中点，S△ABC=
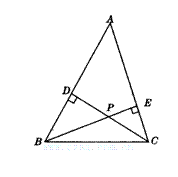
11．（2004年，陕西）如图，在锐角△ABC中，CD、BE分别是AB、AC上的高，且CD、BE交于一点P，若∠A=50°，则∠BPC的度数是（ ）
A．150° B．130° C．120° D．100°
培优作业
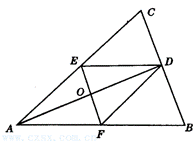
12．（探究题）（1）如图
（2）若将结论与AD是△ABC的角平分线、DE∥AB、DF∥AC中的任一条件交换，所得命题正确吗？
13．（开放题）要使四边形木架（用4根木条钉成）不变形，至少要再钉上几根木条？五边形木架和六边形木架呢？n边形木架呢？
14．（趣味题）《三国演义》中有关木牛流马的叙述：
“孔明即手书一纸，付众观看，众将环绕而视．造木牛之法云：‘方腹曲头，一脚四足；头入领中，舌着于腹．载多而行少，独行者数十里，群行者二十里．曲者为牛头，双者为牛脚，横者为牛领，转者为牛足，覆者为牛背，方者为牛腹，垂者为牛舌，曲者为牛肋，刻者为牛齿，立者为牛角，细者为牛鞅，摄者为牛轴．牛仰双辕，人行六尺，牛行四步．’每牛载十人所食一月之粮，人不大劳，牛不饮食．”
你知道木牛流马中运用了什么数学知识吗？
数学世界
探险家的“难极”
有一个探险家，挖空心思想出一个“难极”来．
什么是探险家的“难极”呢？
一般情况下，如果从某地出发，先往北走100公里，再往东走100公里，然后往南走100公里，这时，终止地总要在出发地正东100公里处．
而若从某地出发，先往北走100公里，再往东走100公里，然后往南走100公里，能正好回到原来的出发地．这个出发地被探险家称其为“难极”．
你知道探险家的“难极”在哪里吗？
答案:
1．A 点拨：锐角三角形的三条高在三角形内部交于一点，直角三角形的三条高交于直角顶点，钝角三角形的三条高在三角形外部交于一点．
2．B 3．AD；△ACD 4．BD，CE，OF 5．C
6．解：∵AD为△ABC的中线，
∴BD=CD，
∴△ABD与△ACD的周长之差为：
（AB+BD+AD）-（AC+CD+AD）=AB-AC=5-3=2（cm）．
7．解：∵∠BAD=∠CAD，∴AD是△ABC的角平分线，DE是△BEC的角平分线．
∵AD⊥BC，垂足为点D，∴AD是△ABC的高，DE是△BEC的高．
∵BD=CD，∴AD是△ABC的中线，DE是△BEC的中线．
点拨：本题是考查三角形的角平分线、中线和高的概念．
8．解：设AB=AC=2x，则AD=CD=x．
（1）AB+AD=15，BC+CD=6时，
有2x+x=15，解得x=5．
∴2x=10，BC=6-5=1．
（2）当BC+CD=15，AB+AD=6时，
有2x+x=6，解得x=2．
∴2x=4，BC=15-2=13．
∵4+4>13，∴此时构不成三角形．
∴这个等腰三角形的腰长及底边长分别为10，1．
点拨：要注意检验结果是否满足三角形三边关系定理．
9．解：方案1：如答图1，在BC上取D、E、F，使BD=ED=EF=FC，连接AE、ED、AF．
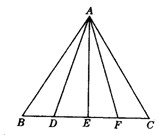
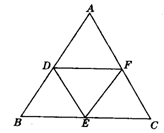
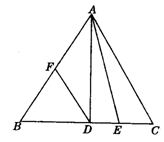
(1) (2) (3)
方案2：如答图2，分别取AB、BC、CA的中点D、E、F，连接DE、EF、DF．
方案3：如答图3，分别取BC的中点D，CD的中点E，AB的中点F，连接AD、AE、DF．同学们，你还有别的方法吗？试试看．
点拨：三角形面积计算公式为×底×高，因此解题的关键是找出底、高分别相等的四个三角形．
10．解：∵AD是△ABC的边BC上的中线，
∴S△ABD=S△ABC=×4=2（cm2）．
∵BE是△ABD的边AD上的中线，
∴S△ABE=S△ABD=×2=1（cm2）．
点拨：三角形的任一中线将三角形分为面积相等的两个小三角形．
11．B 点拨：∵CD、BE分别是AB、AC边上的高，
∴∠AEB=∠CDB=90°，
∵∠A=50°，∴∠ABE=40°，
∴∠BPD=180°-∠CDB-∠ABE=180°-90°-40°=50°，
∴∠BPC=180°-∠BPD=180°-50°=130°．
12．解：（1）DO是△DEF的角平分线．
证明：∵AD是△ABC的角平分线，
∴∠EAD=∠FAD．
∵DE∥AB，DF∥AC，
∴∠EDA=∠FAD，∠FDA=∠EAD（两直线平行，内错角相等）．
∴∠EDA=∠FDA．
∴DO是△DEF的角平分线．
（2）所得命题正确．
13．解：要使四边形木架不变形，至少要再钉上1根木条．
要使五边形木架不变形，至少要再钉上2根木条．
要使六边形木架不变形，至少要再钉上3根木条．
要使n边形木架不变形，至少要再钉上（n-3）根木条．
14．答：用手抬按木牛的双辕或木马的头部，木牛流马会稳稳地向前迈进．
用手操作的时候，人和木牛流马总是呈三角形．
这符合三角形稳定性原理，这也是木牛流马“上山下岭，各尽其便”的原因．
数学世界答案:探险家的“难极”就是南极点．