第八章 二元一次方程组单元测试
姓名：________ 时间：60分钟 满分：100分 评分：________
一、选择题（本大题共12小题，每小题3分，共36分．在每小题所给出的四个选项中，只有一项是符合题目要求）
1．下列方程中，是二元一次方程的是（ ）
A．3x-y2=0
B．
+
=1 C．
-
y=6 D．4xy=3
2．如果2x-7y=8，那么用含y的代数式表示x正确的是（ ）
A．y=
B．y=
C．x=
D．x=
3．方程组
的解是（ ）
A．
B．
C．
D．
4．若4x-3y=0，则
的值为（ ）
A．31 B．-
C．
D．不能确定
5．已知x=2，y=-1是方程2ax-y=3的一个解，则a的值为（ ）
A．2 B．
C．1 D．-1
6．下列各组数中，既是方程2x-y=3的解，又是方程3x+4y=10的解是（ ）
A．
B．
C． D．
7．若xa+1y-2b与-
x2-by2的和是单项式，则a、b的值分别的（
）
A．a=2，b=-1 B．a=2，b=1 C．a=-2，b=1 D．a=-2，b=-1
8．方程3x+2y=5的非负整数解的个数为（ ）
A．1个 B．2个 C．3个 D．4个
9．如果二元一次方程组
的解是二元一次方程2x-3y+12=0的一个解，那么a的值是（
）
A．
B．-
C．
D．-
10．如果（x+y-5）2与│3y-2x+10│互为相反数，那么x、y的值为（ ）
A．x=3，y=2 B．x=2，y=3 C．x=0，y=5 D．x=5，y=0
11．某商场根据市场信息，对商场中现有的两台不同型号的空调进行调价销售，其中一台空调调价后售出可获利10%（相对于进价），另一台空调调价后售出则要亏本10%，这两台空调调价后的售价恰好相同，那么商场把这两台空调调价后售出（ ）
A．既不获利也不赔本; B．可获利1%; C．要亏本2% ; D．要亏本1%
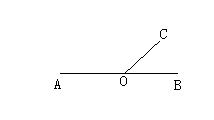12．如图,射线OC的端点O在直线AB上，∠AOC的度数比∠BOC的2倍多10°．设∠AOC和∠BOC的度数分别为x、y，则下列正确的方程组为（ ）
A．
B．
C．
D．
二、填空题（本大题共8小题，每小题3分，共24分．把答案填在题中横线上）
13．已知xm-1+2yn+1=0是二元一次方程，则m=_______，n=________．
14．在等式y=kx+b中，当x=0时，y=-1；当x=1时，y=2，则k=______，b=______．
15．已知m-3n=2m+n-15=1，则m=________，n=________．
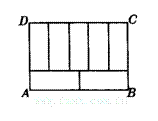
16．如图，周长为68cm的长方形ABCD被分成7个相同的矩形，长方形ABCD的面积为_________．
17．某种植大户计划安排10个劳动力来耕作30亩土地．这些土地可以种蔬菜也可以种水稻，种这些作物所需劳动力及预计产值如下表：
| 每亩所需劳动力（个） | 每亩预计产值（元） | |
| 蔬菜 |
| 3000 |
| 水稻 |
| 700 |
为了使所有土地种上作物，全部劳动力都有工作，应安排种蔬菜的劳动力为______人，这时预计产值为________元．
18．方程组
的解是________．
19．某船在顺水中航行的速度是m千米/时，在逆水中航行的速度是n千米/时，则水流的速度是_________．
20．如果一个两位数的个位数字与十位数字的和为5，那么这样的两位数的个数是________．
三、解答题（本大题共4小题，共40分，解答应写出文字说明，证明过程或演算步骤）
21．解下列方程组．（每小题4分，共16分）
（1）
（2）
（3）
（4）
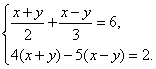
22．（6分）m为正整数，已知二元一次方程组
有整数解，求m．
23．（8分）如图:
24．（10分）“五一”期间，某商场搞优惠促销，决定由顾客抽奖确定折扣，某顾客购买甲、乙两种商品，分别抽到七折（按售价的70%销售）和九折（按售价的90%销售），共付款386元，这两种商品原售价之和为500元．问：这两种商场的原销售价分别为多少元？
答案:
1．C 2．C 3．A
4．B 点拨：∵4x-3y=0，∴4x=3y．
∴=
，故选B．
5．B 点拨：由方程的解的概念知2a×2-（-1）=3．∴a=，故选B．
6．C
7．A 点拨：由题意知xa+1y-2b与-x2-by2是同类项，
∴
解之得
，故选A．
8．A 点拨：由3x+2y=5得y=
．
∵
∴
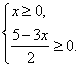解得0≤x≤
．
∴x可得0，1．
当x=0时，y=不合题意，应舍去；
当x=1时，y=
=1．
∴方程3x+2y=5的非负整数解的个数是1，故选A．
9．B 点拨：把a看作已知数，解方程组
解方程组 得
把代入2x-3y+12=0得
2×6a-3×（-3a）+12=0，解得a=-．
10．D 点拨：由互为相反数的概念知
（x+y-5）2+│3y-2x+10│=0．
∴ 
解得
故选D．
11．D 点拨：设调价后售出获利、亏本的两台空调的进价分别为x元、y元，
则（1+10%）x=（1-10%）y．
整理，得x=
y．
∴
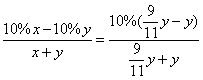=-1%．
即商场要亏本1%，故选D．
12．B 13．2；0 14．3；-1
15．7；2 点拨：已知m-3n=2m+n-15=1，
可得
解得
16．280cm2 点拨：注意观察图形，知2个小长方形的长和5个小长方形的宽相等．
设小长方形的长为xcm，宽为ycm，由题意，得
解得
长方形ABCD的面积为（10+4）×2×10=280（cm2）．
17．5；44000 点拨：设应安排种蔬菜的劳动力为x人，预计产值y元，
由题意，得
解得
18．
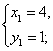
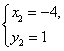
点拨：
①+② 得2│x│=8，∴│x│=4，∴x=±4．
①-② 得2y=2，∴y=1．
∴
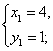
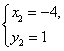
19．
千米/时 20．5个
21．（1）
（2）
（3）
（4）
22．解：解方程组
①+②得（m+3）x=10，∴x=
将x=代入②，得y=
．
∵m为正整数，且方程组的解为整数．
∴m为正整数，且x=与y=同时为整数．
∴m=2，m2=4．
点拨：因为要求的是m，与x，y无关．
所以把m当作已知数，用m表示x，y．
23．解：设一本笔记本需x元，则一枝钢笔需y元，依题意，得
解这个方程，得
答：1本笔记本需2元，1支钢笔需4元．
24．解：设甲、乙两种商品的原销售价分别为x元，y元，依题意，得
解得
答：甲、乙两种商品的原销售价分别是320元、180元．