7．2 与三角形有关的角
7．2．1 三角形的内角
基础过关作业
1．△ABC中，∠A=50°，∠B=60°，则∠C=________．
2．已知三角形的三个内角的度数之比为1：2：3，则这个三角形是（ ）
A．锐角三角形 B．直角三角形 C．钝角三角形 D．不能确定
3．△ABC中，∠A=∠B+∠C，则∠A=______度．
4．根据下列条件，能确定三角形形状的是（ ）
（1）最小内角是20°； （2）最大内角是100°；
（3）最大内角是89°； （4）三个内角都是60°；
（5）有两个内角都是80°．
A．（1）、（2）、（3）、（4） B．（1）、（3）、（4）、（5）
C．（2）、（3）、（4）、（5） D．（1）、（2）、（4）、（5）
5．如图1，∠1+∠2+∠3+∠4=______度．
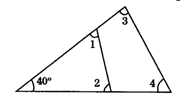
(1) (2) (3)
6．三角形中最大的内角不能小于_______度，最小的内角不能大于______度．
7．△ABC中，∠A是最小的角，∠B是最大的角，且∠B=4∠A，求∠B的取值范围．
8．如图2，在△ABC中，∠BAC=4∠ABC=4∠C，BD⊥AC于D，求∠ABD的度数．
综合创新作业
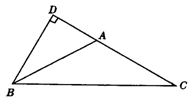
9．（综合题）如图3，在△ABC中，∠B=66°，∠C=54°，AD是∠BAC的平分线，DE平分∠ADC交AC于E，则∠BDE=_________．
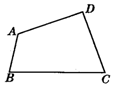
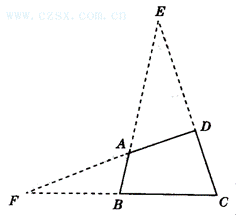
10．（应用题）如图7-2-1-4是一个大型模板，设计要求BA与CD相交成30°角，DA与CB相交成20°角，怎样通过测量∠A，∠B，∠C，∠D的度数，来检验模板是否合格？
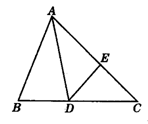
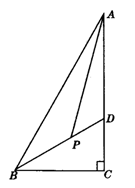
11．（创新题）如图，△ABC中，AD是BC上的高，AE平分∠BAC，∠B=75°，∠C=45°，求∠DAE与∠AEC的度数．
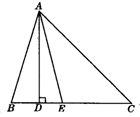
12．（2005年，福建厦门）如图，已知，在直角△ABC中，∠C=90°，BD平分∠ABC且交AC于D．
（1）若∠BAC=30°，求证：AD=BD；（2）若AP平分∠BAC且交BD于P，求∠BPA的度数．
13．（易错题）在△ABC中，已知∠A=
∠B=
∠C，求∠A、∠B、∠C的度数．
培优作业
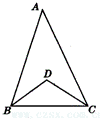
14．（探究题）（1）如图，在△ABC中，∠A=42°，∠ABC和∠ACB的平分线相交于点D，求∠BDC的度数．
（2）在（1）中去掉∠A=42°这个条件，请探究∠BDC和∠A之间的数量关系．
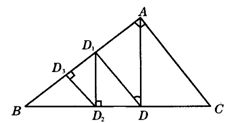
15．（开放题）如图，在直角三角形ABC中，∠BAC=90°，作BC边上的高AD，图中出现多少个直角三角形？又作△ABD中AB边上的高DD1，这时，图中共出现多少个直角三角形？按照同样的方法作下去，作出D1D2，D2D3，…，当作出Dn-1Dn时，图中共出现多少个直角三角形？
数学世界
推门与加水
爱迪生成名以后，去拜访他的人很多，但客人们都感到爱迪生家的大门很重，推门很吃力．后来，一位朋友对他说：“你有没有办法让你家的大门开关起来省力一些？”爱迪生边笑边回答：“我家的大门做得非常合理，我让那个门与一个打水装置相连接，来访的客人，每次推开门都可以往水槽加20升水．”
不仅如此，爱迪生还在想，如果每次推门能向水槽加入25升水的话，那么比原来少推12次门，水槽就可以装满了．
你能算出爱迪生家水槽的容积吗？
答案:
1．70°
2．B 点拨：设这个三角形的三个内角分别为x°、2x°、3x°，
则x+2x+3x=180，解得x=30．
∴3x=90．
∴这个三角形是直角三角形，故选B．
3．90 点拨：由三角形内角和定理知∠A+∠B+∠C=180°，
又∠B+∠C=∠A，∴∠A+∠A=180°，∴∠A=90°．
4．C
5．280 点拨：由三角形内角和定理知，
∠1+∠2=180°-40°=140°，∠3+∠4=180°-40°=140°．
∴∠1+∠2+∠3+∠4=140°×2=280°．
6．60；60
7．解：设∠B=x，则∠A=
x．
由三角形内角和定理，知∠C=180°-
x．
而∠A≤∠C≤∠B．所以x≤180°-x≤x．即80°≤x≤120°．
8．解：设∠ABC=∠C=x°，则∠BAC=4x°．
由三角形内角和定理得4x+x+x=180．
解得x=30．
∴∠BAC=4×30°=120°．
∠BAD=180°-∠BAC=180°-120°=60°．
∴∠ABD=90°-∠BAD=90°-60°=30°．
点拨：∠ABD是Rt△BDA的一个锐角，若能求出另一个锐角∠DAB．
就可运用直角三角形两锐角互余求得．
9．132° 点拨：因为∠BAC=180°-∠B-∠C=180°-66°-54°=60°，
且AD是∠BAC的平分线，所以∠BAD=∠DAC=30°．
在△ABD中，∠ADB=180°-66°-30°=84°．
在△ADC中，∠ADC=180°-54°-30°=96°．
又DE平分∠ADC，所以∠ADE=48°．
故∠BDE=∠ADB+∠ADE=84°+48°=132°．
10．
解：设计方案1：测量∠ABC，∠C，∠CDA，
若180°-（∠ABC+∠C）=30°，180°-（∠C+∠CDA）=20°同时成立，
则模板合格；否则不合格．
设计方案2：测量∠ABC，∠C，∠DAB，
若180°-（∠ABC+∠C）=30°，（∠BAD+∠ABC）-180°=20°同时成立，
则模板合格；否则不合格．
设计方案3：测量∠DAB，∠ABC，∠CDA，
若（∠DAB+∠CDA）-180°=30°，（∠BAD+∠ABC）-180°=20°同时成立，
则模板合格；否则不合格．
设计方案4：测量∠DAB，∠C，∠CDA，
若（∠DAB+∠CDA）-180°=30°，180°-（∠C+∠CDA）=20°同时成立，
则模板合格；否则不合格．
点拨：这是一道几何应用题，借助于三角形知识分析解决问题，对形成用数学的意识解决实际问题是大有益处的．
11．解法1：∵∠B+∠C+∠BAC=180°，∠B=75°，∠C=45°，
∴∠BAC=60°．
∵AE平分∠BAC，∴∠BAE=∠CAE=
∠BAC=×60°=30°．
∵AD是BC上的高，∴∠B+∠BAD=90°，
∴∠BAD=90°-∠B=90°-75°=15°，
∴∠DAE=∠BAE-∠BAD=30°-15°=15°．
在△AEC中，∠AEC=180°-∠C-∠CAE=180°-45°-30°=105°．
解法2：同解法1，得出∠BAC=60°．
∵AE平分∠BAC，∴∠EAC=∠BAC=×60°=30°．
∵AD是BC上的高，∴∠C+∠CAD=90°，
∴∠CAD=90°-45°=45°，∴∠DAE=∠CAD-∠CAE=45°-30°=15°．
∵∠AEC+∠C+∠EAC=180°，
∴∠AEC+30°+45°=180°，∴∠AEC=105°．
答：∠DAE=15°，∠AEC=105°．
点拨：本节知识多与角平分线的定义，余角的性质，平行线的性质，三角形高的定义综合应用，有时也结合方程组、不等式等代数知识综合应用．求角的度数的关键是把已知角放在三角形中，利用三角形内角和定理求解，或转化为与已知角有互余关系或互补关系求解，有些题目还可以转化为已知角的和或差来求解．
12．（1）证明：∵∠BAC=30°，∠C=90°，
∴∠ABC=60°．
又∵BD平分∠ABC，∴∠ABD=30°．
∴∠BAC=∠ABD，∴BD=AD．
（2）解法1：∵∠C=90°，
∴∠BAC+∠ABC=90°．
∴（∠BAC+∠ABC）=45°．
∵BD平分∠ABC，AP平分∠BAC，
∴∠BAP=∠BAC，∠ABP=∠ABC；
即∠BAP+∠ABP=45°，
∴∠APB=180°-45°=135°．
解法2：∵∠C=90°，
∴∠BAC+∠ABC=90°．
∴（∠BAC+∠ABC）=45°．
∵BD平分∠ABC，AP平分∠BAC，
∴∠DBC=∠ABC，∠PAC=∠BAC，
∴∠DBC+∠PAD=45°．
∴∠APB=∠PDA+∠PAD=∠DBC+∠C+∠PAD=∠DBC+∠PAD+∠C=45°+90°=135°．
13．解：由∠A=∠B=∠C知，∠B=3∠A，∠C=5∠A．
设∠A=x°，则∠B=3x°，∠C=5x°．
由三角形内角和定理得x+3x+5x=180．
解得x=20．
∴3x=60，5x=100．
∴∠A=20°，∠B=60°，∠C=100°．
点拨：解此类题，一般设较小的角为未知数．
14．解：（1）∵∠A=42°，
∴∠ABC+∠ACB=180°-∠A=138°．
∵BD、CD平分∠ABC、∠ACB的平分线．
∴∠DBC=∠ABC，∠DCB=∠ACB．
∴∠DBC+∠DCB=（∠ABC+∠ACB）=×138°=69°．
∴∠BDC=180°-（∠DBC+∠DCB）=180°-69°=111°．
（2）∠BDC=90°+∠A．
理由：∵BD、CD分别为∠ABC、∠ACB的平分线，
∴∠DBC=∠ABC，∠DCB=∠ACB．
∴∠DBC+∠DCB=（∠ABC+∠ACB）=（180°-∠A）=90°-∠A．
∴∠BDC=180°-（∠DBC+∠DCB）
=180°-（90°-∠A）
=90°+∠A．
点拨：欲求∠BDC，只要求出∠DBC+∠DCB即可．
15．解：作出BC边上的高AD时，图中出现3个直角三角形；
作出△ABD中AB边上的高DD1时，图中出现5个直角三角形；
作出Dn-1Dn时，图中共出现（2n+3）个直角三角形．
数学世界答案:
设原来推门x次可把水槽装满水，由题意，得20x=25（x-12）．
解得x=60．
则水槽容积为20×60=1200（升）．