华师大版七年级下第七章《二元一次方程》测评卷
一、填空题（每题3分，共30分）
1． 若
是关于x、y的二元一次方程，则
=________.
2． 一个长方形的周长为60cm，长比宽的2倍还多6cm，则该长方形的长是________,宽是__________.
3． 若
，则
______。
4． 当
________时，方程组
的解满足
.
5． 0
6． 已知两个单项式
与
能合并为一个单项式，则
____，
。
7． 若
与
互为相反数，且
，则
_________。
8． 甲、乙两名运动员练习赛跑，如果甲让乙先跑10米，那么甲跑5秒就能追上乙；如果甲让乙先跑10米，那么甲跑15米才能追上乙。设甲、乙的速度分别为米／秒，米 /秒，列方程组得____________。
二、选择题（每题３分，共24分）
１． 下列方程中是二元一次方程的是（ ）
A. 
B. 
C. 
D.
2. 若方程
的解是正整数，则一定是（ ）
A.偶数 B.奇数 C.整数 D.正整数
3. 下列说法正确的是（ ）
A. 
的解也是方程组
的解 B. 
的解也是方程组的解
C．方程组的解是和的解 D．有无数个正整数解
4. 已知
，
，用含的代数式表示的结果是（ ）
A.
B. 
C. 
D. 
5. 方程■
是二元一次方程，■是被弄污的的系数，请你推断■的值属于下列情况中的（ ）
A.不可能是-1 B. 不可能是-2 C.不可能是1 D. 不可能是2
6. 如果
+
=0成立，那么
=（ ）
A.1 B. 2 C.9 D.16
7. 已知
和
是同类项，则
与
的大小关系是（ ）
A.
> B. = C. < D.不能确定
8. 已知
是方程组
的解，则
、
分别为（ ）
A． 
B． 
C．
D． 
三、解方程组（每题4分，共16分）
1、
2、
3、
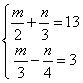4、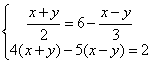
四、解答题（1、2题各4分，3、4题各5分，5、6题各6分，共30分）
1、
当
为何值时，三个二元一次方程
，
和
有公共解？
2、
在公式
中，当
时，
；当
时，
。求：当
时，
的值是多少？
3、 光明中学现有校舍面积20000平方米，为改善办学条件，计划拆除部分旧校舍，建造新校舍，使新校舍的面积比拆除旧校舍面积的3倍还多1000平方米，这样建造后就使校舍总面积比原有校舍面积增加20%，求学校拆除旧校舍和建造新校舍分别是多少平方米？
4、 有一批足球迷来到一家旅社，当领队安排住房时，发现这样一个问题；若每间客房住2人，则有10人无房间住；若每间客房住3人，则有5间客房无人住。你能算出这批足球迷的人数和旅社客房的间数吗？
5、 某校为了促进学生参加体育活动，举办了一次乒乓球比赛，每赛一场的记分及奖励方案如下表；当比赛进行到第12场（也是最后一场）时，七年级甲班的李宏同学共积19分。
| 标准 | 胜一场 | 平一场 | 负一场 |
| 积分 | 3 | 1 | 0 |
| 奖励 （元） | 1.5 | 0.7 | 0 |
（1） 试通过计算，判断李宏同学胜、平、负各几场？
（2） 设李宏同学获得的奖金为w元，试求w的最大值。
6、 下表所示为装运甲、乙、丙三种蔬菜的重量及利润。某汽运公司计划装运甲、乙、丙三种蔬菜到外地销售（每辆汽车按规定满载，且每辆汽车只能装一种蔬菜）
（1） 若用8辆汽车装运乙、丙两种蔬菜11吨到A地销售，问装运的汽车各多少辆？
| 甲 | 乙 | 丙 | |
| 每辆汽车能装满的吨数 | 2 | 1 | 1.5 |
| 每吨蔬菜可获利润（百元） | 5 | 7 | 4 |
（2） 计划用20辆汽车装运甲、乙、丙三种蔬菜36吨到B地销售，如何安排装运，可使公司获得100个百元的利润？
