苏教版七年级数学下第八九章检测
知识点：
1、 同底数幂的乘法法则
(m、n是正整数)
2、 幂的乘方法则
(m、n是正整数)
3、 积的乘方法则
(n是正整数)
4、 同底数幂的除法法则
(m、n是正整数，m >n)
5、 扩展
(m、n、p是正整数)
6、 零指数和负指数法则
(
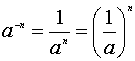，n是正整数)
7、 科学记数法
(1≤a <10，a为整数)
8、 项式乘单项式：
单项式与单项式相乘，把它们的系数、相同字母的幂分别相乘，对于只在一个单
项式里含有的字母，则连同它的指数作为积的一个因式。
9、 单项式乘多项式：
单项式与多项式相乘，用单项式乘多项式的的每一项，再把所得的积相加。
m(a+b－c)＝ma+mb－mc
10、 多项式乘多项式：
多项式与多项式相乘，先用一个多项式的每一项乘另一个多项式的每一项，
再把所得的积相加。
(a+b)(c+d)=ac+ad+bc+bd
11、 乘法公式：
a) 完全平方公式：(a+b)2=a2+2ab+b2； (a -b)2=a2-2ab+b2
平方差公式： (a+b)(a-b)=a2-b2
12、 因式分解：
i. 把一个多项式写成几个整式的积的形式叫做多项式的因式分解。
ii. 多项式的乘法与多项式因式分解的区别
简单地说：乘法是积化和，因式分解是和化积。
（3）因式分解的方法：
①提公因式法； ②运用公式法。
13、因式分解的应用：
（1）提公因式法：如果多项式的各项含有公因式，那么就可以把这个公因式提出来。把多项式化成公因式与另一个多项式的积的形式，这种分解因式的方法叫做提公因式法。
（2）公因式：多项式ab＋ac＋ad的各项ab、ac、ad都含有相同的因式a，a称为多项式各项的公因式。
（3）用提公因式法时的注意点：
① 公因式要提尽，考虑的顺序是，先系数，再单独字母，最后多项式。如：
② 当多项式的第一项的系数为负数时，把“－”号作为公因式的负号写在括号外，使括号内的第一项的系数为正。如：
③ 提公因式后，另一个多项式的求法是用原多项式除以公因式。
（4）运用公式法的公式：
① 平方差公式：a2-b2=(a+b)(a-b)
② 完全平方公式： a2+2ab+b2=(a+b)
（5）因式分解的步骤和要求：
把一个多项式分解因式时，应先提公因式，注意公因式要提尽，然后再应用公式，如果是二项式考虑用平方差公式，如果是三项式考虑用完全平方公式，直到把每一个因式都分解到不能再分解为止。
如：-2x5y+4x3y3-2xy5=-2xy(x4-2x2y2+y4)=-2xy(x2-y2)(x2+y2)=-2xy(x+y)(x-y)(x2+y2)
苏教版七年级数学下第八章~第九章检测
一、填空题（每题2分，共20分）
1、a 3·a =_______，a 3÷a= 。
2、5 0＝ ，2 －1＝ 。
3、计算：(－x4)3=_______，－
4、计算：2005 2－2004×2006＝ ，3.14×98－3.14×10＋12×3.14＝ 。
5、因式分解：(1)
(2)－x 2＋2xy－y 2 ＝ 。
6、用科学记数法表示
(1)氢原子中电子和原子核之间的距离为0.厘米，用科学记数法表示这个距离为 厘米；
(2)用科学记数法表示： (4×102)×(8×106)的结果是_______ ______。
7、已知
，则x 2＋y 2＝
，xy＝ 。
8、计算：214×(－ )7＝ 。
9、已知23x+2＝64，则x的值是 。
10、如果等式（
的值为
。
二、选择题（每题3分，共18分）
11、下列计算：（1）an·an=2an； (2) a6+a6=a12； (3) c·c5=c5 ；
(4) 3b3·4b4=12b12 ； (5) (3xy3)2=6x2y6
正确的个数为 （ ）
A、0
B、
12、下列因式计算得代数式xy 2－9x的是 （ ）
A、x(y－3) 2 B、x(y＋3) 2
C、x(y＋3)(y－3) D、x(y＋9)(y－9)
13、下列各多项式中，能用平方差公式分解因式的是 （ ）
A、
B、
C、
D、
14、若a＝－0.3 2，b＝－3－2，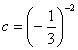
，
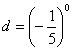，则
（ ）
A、a＜b＜c＜d B、b＜a＜d＜c C、a＜d＜c＜b D、c＜a＜d＜b
15、已知am=3，an=2，那么am+n+2的值为 （ ）
A、8
B、
16、如左图，在边长为的正方形中挖掉一个边长为
的小正方形(
，把余下的部分剪拼成一矩形如右图，通过计算两个图形(阴影部分)的面积，验证了一个等式，则这个等式是
（ ）
A、
B、
C、
D、
三、计算题（每题4分，共24分）
17、－t·(－t) 2－t 3
18、a3·a3·a2+(a4)2＋(－
19、(x＋1)(x－1)(x 2＋1) 20、(a－2b＋c)(a＋2b－c)
21、(x－1)(x 2＋x＋1) 22、3（a＋5b）2－2(a－b) 2
四、因式分解（每题4分，共16分）
23、
24、9(a＋b) 2－(a－b) 2
25、a 2(x－y)＋b2(y－x)
26、
五、解答题(27、28、30题各5分，29题3分，31题各4分，共22分)
27、已知a－b＝－1，ab＝3，求a 3b－
28、观察下列等式，你会发现什么规律：
，
，
，
，……
请将你发现的规律用仅含字母n（n为正整数）的等式表示出来，并说明它的正确性。
你发现的规律是 。
说明：
29、多项式x 2＋1加上一个整式后是含x的二项式的完全平方式。
例题：x 2＋1＋ 2x ＝（ x＋1 ）2。
（1）按上例再写出两个加上一个单项式后是含x的二项式的完全平方式的式子（不能用已知的例题）：
①x 2＋1＋ ＝（ ）2；
②x 2＋1＋ ＝（ ）2。
（2）按上例写出一个加上一个多项式后是一个含x的二项式的完全平方式
x 2＋1＋ ＝（ ）2
30、已知：a、b、c分别为ΔABC的三条边的长度，请用所学知识说明：（a －c ）2－b 2是正数、负数或零。
31、阅读下列一段话，并解决后面的问题。
观察下面一列数：
1，2，4，8，……
我们发现，这列数从第二项起，每一项与它前一项的比值都是2。我们把这样的一列数叫做等比数列，这个共同的比值叫做等比数列的公比。
（1）等比数列5，―15，45，…的第4项是 ；
（2）如果一列数a1,a2,a3,…是等比数列，且公比是q，那么根据上述规定有
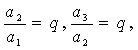
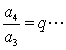
所以
＝
q，
＝q＝·q ·q＝ q 2，
＝q＝ q 2·q＝ q 3，……
则an= (用a1与q的代数式表示)
（3）一个等比数列的第2项是10，第3项是20，求它的第1项和第4项。
解答：
1、a 4，a 2
2、1，
3、－x 12，－
4、1，314
5、
6、5.29×10 －9，3.2×10 9
7、12，3
8、－1
9、
10、－2，1，0
11、A 12、C 13、C 14、B 15、C 16、D
17、－t·(－t) 2－t 3 ＝－t·t 2－t 3 ＝－t 3－t 3＝－2 t 3
18、a3·a3·a2+(a4)2＋(－
19、(x＋1)(x－1)(x 2＋1) ＝(x 2－1) (x 2＋1) ＝x 4－1
20、(a－2b＋c)(a＋2b－c) ＝[a－（2b－c）] [a＋（2b－c）]＝a 2－（2b－c）2
＝a 2－（4b 2－4b c＋c 2）＝a 2－4b 2＋4b c－c 2
21、(x－1)(x 2＋x＋1) ＝x 3＋x 2＋x－x 2－x－1＝x 3－1
22、3（a＋5b）2－2(a－b) 2＝3（a 2＋
＝
＝a 2＋
23、＝
24、9(a＋b) 2－(a－b) 2＝［３(a＋b)］2－(a－b) 2
＝［３(a＋b)＋(a－b)］［３(a＋b)－(a－b)］
＝(
＝４(
25、a 2(x－y)＋b2(y－x) ＝a 2(x－y)－b2(x－y)
＝(x－y)（a 2－b2）
＝(x－y) （a ＋b）（a －b）
26、＝（x 2＋4）2－（4x）2
＝[（x 2＋4）＋4x][（x 2＋4）2－4x]
＝（x 2＋4x ＋4）（x 2－4x＋4）
＝（x＋2）2（x－2）2
27、a 3b－
＝ab（a－b）2
＝3×（－1）2
28、n（n＋2）＋1＝（n＋1）2
n（n＋2）＋1＝n 2＋2n＋1＝（n＋1）2
29、x 2＋1＋ －2 x ＝（ x＋1 ）2
x 2＋1＋
x 4 ＝（ x 2＋1
）2
x 2＋1＋ x 4＋x 2 ＝（ x 2＋1 ）2
30、（a －c ）2－b 2＝（a －c ＋b）（ a －c－b）
∵a、b、c分别为ΔABC的三边
∴a＋b＞c，b＋c＞a
∴a－c＋b＞0，a －c－b＜0
∴（a －c ＋b）（ a －c－b）＜0
∴（a －c ）2－b 2是负数
31、（1）－135
（2） q n－1
(3) ∵ ＝q＝10，＝ q 2＝20
∴（ q 2）÷（q）＝20÷10
∴q＝2，＝5