| 课题 | 小结与复习 | 时:2005________ | |
| 教学目标 | 使学生对整章的学习内容做一回顾，系统地把握全章的知识要点和基本技能。 2．通过例题和练习，使学生能较好地运用本章知识和技能解决有关问题。 | ||
| 教学重点 | 判断图形是否是轴对称图形，线段的垂直平分线、角平分线的性质、等腰三角形的性质和判定及其应用 | ||
| 教学难点 | 而灵活运用上述性质解决问题、轴对称图案的设计 | ||
| 教学方法 | |||
| 教学用具 | 、几何做一个最好用课件！！！！ | ||
| 环保教育 | |||
教学过程：一、复习引入
二：创设情境，提出问题，引入新课
三：新课：(教师板书板书)(课堂练习)
一、知识回顾
问题1：轴对称图形的定义是什么?
它是判断图形是否是轴对称图形的依据。
问题2：是否会画轴对称图形的对称轴?
找出轴对称图形的任一组对称点，连结对称点，画对称点所连线段的垂直平分线，即得到该图形对称轴。
问题3：轴对称图形对称点的连线与对称轴有什么关系?
轴对称图形对称点的连线被对称轴垂直平分。
问题4：线段垂直平分线、角平分线具有什么性质?
线段垂直平分线上的点到线段两端的距离相等；角平分线上的点到角两边的距离相等。
问题5：等腰三角形有什么性质?
等腰三角形底边的中线、高线、顶角的平分线互相重合，等腰三角形的两个底角相等(等边对等角)，等边三角形的三个角都等于60°。
问题6：如何判断三角形是等腰三角形?等边三角形?
如果一个三角形有两个角相等，那么这两个角所对的边也相等(等角对等边)；有两个角是60°的三角形是等边三角形，有一个角是60°的等腰三角形是等边三角形。
二、例题
1．下列图案是轴对称图形的有( )
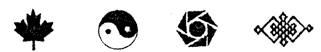
A．1个 D．2个 C．3个 D．4个
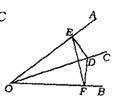2．如右图所示，已知，OC平分∠AOB，D是OC上一点，DE⊥OA，DF⊥OB，垂足为E、F点，那么
(1)∠DEF与∠DFE相等吗?为什么?
(2)OE与OF相等吗?为什么?
三、巩固练习
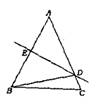
如右图所示，已知AB＝AC，DE垂直平分AB交AC、AB于D、E两点，若AB＝12cm，BC＝l0cm，∠A＝49°14′54″.求△BCD的周长和∠DBC度数。
四、课堂小结
通过本节课复习，同学们应掌握本章知识和技能，并运用所学知识和技能解决问题，
五、作业
巩固练习
| 教学小结 | 初步认识 |
本章教学要求
1．要求同学们经过观察、动手操作掌握轴对称图形以及关于直线成轴对称这两个概念。
2．熟悉常见的几个轴对称图形，会画轴对称图形的对称轴以及简单平面图形经过一次轴对称后的图形，能利用轴对称设计简单的图形。探索并了解轴对称的基本性质。
3．掌握线段、角和圆等常见图形的轴对称性。
线段：线段是轴对称图形，对称轴是线段中垂线和本身所在直线。
线段垂直平分线上的点到这条线段两端点的距离相等。
到线段两端点的距离相等的点在这条线段的垂直平分线上。
角：是轴对称图形，对称轴是角平分线所在直线。
角平分线上的点到角两边的距离相等。
到角两边的距离相等的点在这个角的平分线上。
4．了解等腰三角形的概念，探索并掌握等腰三角形的性质以及识别方法。
性质：
①等腰三角形的两个底角相等 （简写成等边对等角 ）
②等腰三角形的顶角平分线、底边上的中线和高线互相重合（简称三线合一）
识别方法：
（1）用定义识别：有两条边相等的三角形是等腰三角形
（2）等角对等边：如果一个三角形有两个角相等，那么这两个角所对的边也相等。
6．了解等边三角形的概念，探索并了解等边三角形的性质以及识别方法。
性质： 等边三角形的每个角都是600
识别方法：
三个角都相等的三角形是等边三角形。
有一个角是600的等腰三角形是等边三角形。
|
| |
| 本周强化练习： | |
一．填空题
1．下列图形中，一定是轴对称图形的有（ ）个。
线段、三角形、平行四边形、梯形，半圆
2．观察下面的英文字母，其中是轴对称图形的有（ ）个。
A，C，D，E，F，H，J，S，M，Y，Z
3．等腰三角形的一个内角是700，则它的另外两个角的度数分别是（ ）。
4. 已知1，3，x分别为等腰△ABC的三边长，化简
（ ）
5. 等腰三角形的一个外角是40度，则这个等腰三角形的底角等于（ ）度。
6．如图，三角形ABC中，AB=AC，∠A=40度，AB的垂直
平分线MN交AC于D，连接BD，∠DBC等于（ ）度
7．写出两个成轴对称图形的汉字，（ ）和（ ）
8．等腰三角形的周长为17厘米，一条边的长为3厘米，
则这个等腰三角形的底边长为（ ）厘米。
二．选择题
9．下列说法中正确的是（ ）
A．等腰三角形的角平分线、中线、高三线合一。
B．等腰三角形的可以是锐角三角形也可以是钝角三角形。
C．若一个三角形有两个底角相等，则这个三角形是等腰三角形。
D．等腰三角形的腰大于底边的一半。
10．如图，AE平分∠BAC，DE∥AB，AD=DC，
则△ABC是（ ）
A. 直角三角形 B .锐角三角形
C. 等腰三角形 D.等边三角形
11.下面四个图形中 ,哪个不是轴对称图形 ( )
A. 有一个内角是45度的直角三角形.
B. 有两个内角相等的三角形.
C. 有一个内角是30度的直角三角形
D. 一个三角形的两个内角分别为300,1200
12. 下列关于等腰三角形的判断错误的是( )
A. 底角可以是锐角 B. 外角中最多有一个锐角
C. 底角可以大于直角 D. 外角中可以有三个钝角
13.一个等腰三角形但不是等边三角形,它的角平分线、高线、中线总数共（ ）条
A．9 B. 7 C. 6 D. 3
三. 解答题
14．如图,△ABC中,∠ABC=1200,AM=AN,CN=CP,
求 ∠MNP的度数.
15. 公园里两条小河MO、NO在O处汇合，两河形成的半岛上有一处古迹P如图，现计划在两条小河上各建一座小桥Q和R，并在半岛上修三段小路，连通两座小桥与古迹，这两座小桥应建在何处，才能使修路费用最少？
16． 已知AD是等腰三角形一腰上的高，∠DAB=600，求△ABC的三个内角的度数。
17．如图,△ABC中,AD平分∠CAB交BC于D，且CD=2，∠C=900，∠DEF=900，∠B=∠FDB=22.50,AE=6,DF=4,求AB的长.
四.证明题
18. 如图,△ABC中,AB=AC,E 在CA的延长线上,∠AEF=∠AFE,求证:EF⊥BC
五.选做题
1. △ABC中,AB=AC,且过△ABC某一点的直线可将△ABC分成两个等腰三角形,求△ABC各内角的度数.
2.
将图中的三角形纸片沿虚线折叠得的粗实线图形面积与原三角形面积之比为2:3,已知图中三个阴影的三角形的面积之和为1,试确定重叠部分的面积.
参考答案：
1. 2个
2. 7
3. 400,700或550,550
4. 5
5. 20
6. 300
7. 略
8. 3
9. D 10. C 11. C 12. C 13. B 14. 300
15. 作古迹P关于OM的对称点P’ 关于ON的对称点P’’ ,连接P’P’’ ,交OM于Q,交ON于R,则Q,R就是所选的桥址.
16. ( 300
, 300 ,1200)
, ( 150 , 1500 ,150), ( 750 , 300 ,750) 提示:有下列三种图形:
 | |||
 | |||
17. 12 提示:证CE=DE,DE=EF,DF=BF
18. 提示: 过A点作AM⊥BC,交BC于M.,证∠BAM=∠EFA,即AM∥EF
选做题:
1.有四种情况
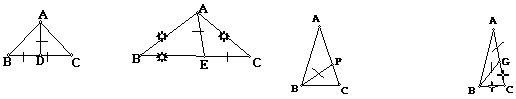( 450
, 450 ,900) ,
( 360 , 3600 ,1080), ( 360 , 720 ,720) , (
,
,)
|
2. 1 设重叠部分的面积为x,列方程.