初一数学(二元一次方程组)单元测试题
班级 姓名 学号 成绩
一.填空题:(每小题2分,共10小题20分)
1.已知![]() ,则用
,则用![]() 的代数式表示
的代数式表示![]() ,得
;其中当
,得
;其中当![]() 时,
时,![]() =
。
=
。
2.若![]() 是二元一次方程,则
是二元一次方程,则![]() = ;
= ;![]() = 。
= 。
3.已知![]() ,则
,则![]() = 。
= 。
4.若![]() 是方程
是方程![]() 的一个解,则
的一个解,则![]() = 。
= 。
5.已知![]() 与
与![]() 的和是一个单项式,则
的和是一个单项式,则![]() = ,
= ,![]() = 。
= 。
6.已知方程![]() 。
。
当![]() = 时,该方程为一元一次方程;当
= 时,该方程为一元一次方程;当![]() = 时,该方程为二元一次方程。
= 时,该方程为二元一次方程。
7.已知![]() ,则
,则![]() = ,
= ,![]() = 。
= 。
8.已知![]() ,若
,若![]() ,则
,则![]() ;若
;若![]() 时,则
时,则![]() 。那么
。那么![]() 的值是
。
的值是
。
9.若![]() (
(![]() ),则
),则![]() = 。
= 。
10.若![]() ,则
,则![]() =
。
=
。
二.选择题:(每小题 2分,共10小题20分)
11.下列方程组① 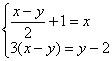 、②
、② ![]() 、③
、③ ![]() 、④
、④ 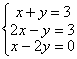 、⑤
、⑤![]() 、⑥
、⑥ ![]() (其中
(其中![]() 、
、![]() 为未知数) 中,是二元一次方程组的有 ( )
为未知数) 中,是二元一次方程组的有 ( )
A.6个 B.5个 C.4个 D.3个
12.在下面四个方程组中,以![]() 为解的方程组是
( )
为解的方程组是
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
13.已知![]() ,当
,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,则
( )
,则
( )
A.![]() ,
,![]() B.
B.![]() ,
,![]() C.
C.![]() ,
,![]() D.
D.![]() ,
,![]()
14.二元一次方程![]() ( )
( )
A.有一个解且只有一个解 B.有二个解且只有二个解 C.无解 D.有无数个解
15.有一个二位正整数,它的十位上的数字与个位上的数字的和是6,这样的二位正整数有
A.3个 B.5个 C.6个 D.无数个 ( )
16.学校篮球数比排球数的2倍少3个,篮球数与排球数的比是3:2,要求这两种球的个数。若设篮球有![]() 个,排球有
个,排球有![]() 个,则根据题意,得到的方程组是
( )
个,则根据题意,得到的方程组是
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
17.已知方程组![]() 的解中
的解中![]() 与
与![]() 的和为2,则
的和为2,则![]() 的值是
( )
的值是
( )
A.6 B.4 C.2 D.0
18.已知![]() 为奇数,
为奇数,![]() 是偶数,方程组
是偶数,方程组![]() 的解
的解![]() 是整数,那么 ( )
是整数,那么 ( )
A .![]() 、
、![]() 都是偶数
B.
都是偶数
B.![]() 、
、![]() 都是奇数 C.
都是奇数 C.![]() 偶,
偶,![]() 奇 D.
奇 D.![]() 奇,
奇,![]() 偶
偶
19.由方程组![]() ,可得
,可得![]() :
:![]() :
:![]() 是
( )
是
( )
A ![]() B
B ![]() C
C ![]() D
D ![]()
20.某次数学竞赛共出了25道选择题,评分办法是:答对一道加4分,答错一道倒扣1分,不答记0分。已知小王不答的题比答错的题多2道,他的总分是74分,则他答对了
A.18题 B.19题 C.20题 D.21题 ( )
三.解方程组:(每小题4分,共6小题24分)
21. ![]() 22.
22.![]()
23.![]() 24.
24.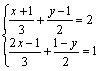
25.![]() 26.
26.![]()
四.解答题:(第27—32题,每题5分,第33题6分,共36分)
27.已知![]() ,
,![]() ,求
,求![]() 的值。
的值。
28.已知方程组![]() 和方程组
和方程组![]() 的解相同,求
的解相同,求![]() 的值。
的值。
29.在代数式![]() 中,当
中,当![]() ,
,![]() 时,其值为5;当
时,其值为5;当![]() ,
,![]() 时,其值为
时,其值为![]() 。求当
。求当![]() ,
,![]() 时,这个代数式的值。
时,这个代数式的值。
30.甲乙两人各购买了新书若干本,已知甲购买的新书比乙的2倍少6本,如果甲给乙9本,则乙是甲的2倍。问甲乙两人各买了几本新书?
31.某班同学参加运土劳动,女生抬土,每两人抬一筐;男生挑土,每人挑两筐。已知全班共用箩筐59只,扁担36根。问全班有多少男生、多少女生?
32.某商场计划拔款9万元从厂家购进50台电视机。已知该厂家生产三种不同型号的电视机,出厂价为:甲种每台1500元,乙种每台2100元,丙种每台2500元。
(1)若商场同时购进其中的两种不同型号的电视机50台,用去9万元,请你研究一下,商场的进货方案;
(2)若商场销售一台甲种电视机可获利150元,销售一台乙种电视机每台可获利200元,销售一台丙种电视机每台可获利250元。在同时购进两种不同型号的电视机的方案中,为了使销售时获利最大,你选择哪一种进货方案?
30.要使方程组![]() 有正整数解,求整数
有正整数解,求整数![]() 的值。
的值。