第九章《多边形》复习题
[一] 认识三角形
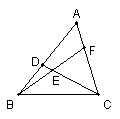
1、图中共有（ ）个三角形。
A：5 B：6 C：7 D：8
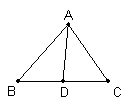
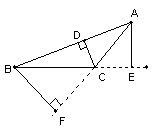2、如图，AE⊥BC，BF⊥AC，CD⊥AB，则△ABC中AC边上的高是哪条垂线段。（ ）
A：AE B：CD C：BF D：AF
3、三角形一边上的高（ ）。
A：必在三角形内部 B：必在三角形的边上
C：必在三角形外部 D：以上三种情况都有可能
4、能将三角形的面积分成相等的两部分的是（ ）。
A：三角形的角平分线 B：三角形的中线 C：三角形的高线 D：以上都不对
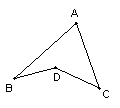
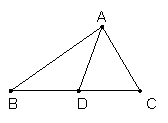5、如图，AD是△ABC的中线，已知△ABD比△ACD的周长大6 cm , 则AB与AC的差为（ ）。
A： 2 cm B：3 cm
C：6 cm D：12 cm
6、具备下列条件的三角形中，不是直角三角形的是（ ）。
A：∠A+∠B=∠C B：∠A=∠B=
∠C
C：∠A=90°-∠B D：∠A-∠B=90°
7、一个三角形最多有 个直角，有 个钝角，有 个锐角。
8、△ABC的周长是12 cm ，边长分别为a ，b , c , 且 a=b+1 , b=c+1 ，
则a= cm , b= cm , c= cm。
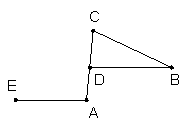
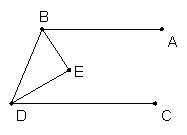9、如图，AB∥CD，∠ABD、∠BDC的平分线交于E，试判断△BED的形状？
[二] 三角形的内、外角和定理及其推论的应用
1、下列说法错误的是（ ）。
A：一个三角形中至少有两个锐角
B：一个三角形中，一定有一个外角大于其中的一个内角
C：在一个三角形中至少有一个角大于60°
D：锐角三角形，任何两个内角的和均大于90°
2、一个三角形的外角恰好等于和它相邻的内角，则这个三角形是（ ）。
A：锐角三角形 B：直角三角形 C：钝角三角形 D：不能确定
3、直角三角形两锐角的平分线相交所成的钝角是（ ）。
A：120° B： 135° C：150° D： 165°
4、△
中，
，则
5、在△ABC中，∠A=100°，∠B-∠C=40°，则∠B= ，∠C= 。
6、如图1，∠B=50°，∠C=60°，AD为△ABC的角平分线，求∠ADB的度数。
7、如图2，∠A=85°，∠B=25°，∠C=35°，求∠BDC的度数。
8、已知：如图3，AE∥BD，∠B=28°，∠A=95°，求∠C的度数。
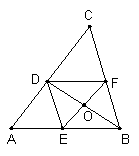9、如图，BD是△ABC的角平分线，DE∥BC，DF∥AB，EF交BD于点O，试问：DO是否是△DEF的角平分线？如果是，请给予证明；如果不是，请说明理由。
[三]三角形三边关系的应用
1、以下列线段为边不能组成等腰三角形的是（ ）。
A：
、、
B：
、
、 C：、、
D：
、、
2、现有两根木棒，它们的长度分别为40 cm和50 cm，若要钉成一个三角架，则在下列四根棒中应选取（ ）。
A：10 cm 的木棒 B：40 cm 的木棒 C：90 cm 的木棒 D：100 cm 的木棒
3、三条线段a=5,b=3,c为整数，从a、b、c为边组成的三角形共有（ ）.
A：3个 B：5个 C：无数多个 D： 无法确定
4、等腰三角形的两边长为25cm和12cm ，那么它的第三边长为 cm 。
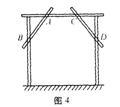5、工人师傅在做完门框后．为防变形常常像图4中所示的那样上两条斜拉的木条 （即图4中的AB，CD两根木条），
这样做根据的数学道理是 。
[四]多边形的内、外角和定理的综合应用
1、若四边形的四个内角大小之比为1：2：3：4，则这四个内角的大小为 。
2、如果六边形的各个内角都相等，那么它的一个内角是 。
3、在各个内角都相等的多边形中，一个外角等于一个内角的
，则这个多边形的每个内角为 度。
4、（n+1）边形的内角和比n边形的内角和大（ ）。
A： 180° B： 360° C：n×180° D: n×360°
5、n边形的内角中，最多有（ ）个锐角。
A：1个 B： 2 个 C： 3个 D： 4个
6、设有一个凸多边形，除去一个内角以外的所有其他内角之和为2570°，则该内角为（ ）。
A： 90° B： 105° C： 120° D: 130°
7、若多边形内角和分别为下列度数时，试分别求出多边形的边数。
① 1260° ② 2160°
8、已知n边形的内角和与外角和之比为9:2，求n。
[五]用正多边形拼地板
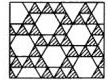1、用正三角形和正方形组合能够铺满地面，每个顶点周围有
个正三角形和 个正方形。
2、任意的三角形、 也能铺满平面。
3、如图，平面镶嵌中的正多边形是 。
4、下列正多边形地砖中不能铺满地面的正多边形是（ ）。
A：正三角形 B：正四边形 C：正五边形 D：正六边形
5、若铺满地面的瓷砖每一个顶点处由6块相同的正多边形组成，此时的正多边形只能是（ ）。
A：正三角形 B：正四边形 C：正六边形 D：正八边形