二元一次方程练习题 班级 姓名
一、填空题(每题3分,共24分)
1、
如果单项式x![]() y与x
y与x![]() y
y![]() 是同类项,则m= ,n= 。
是同类项,则m= ,n= 。
2、 如果2x-7y=8,那么用y表示x得 。
3、
方程组![]() 的解是
。
的解是
。
4、
如果︱x-2︱+(x-y+3)![]() =0那么(x+y)
=0那么(x+y)![]() = 。
= 。
5、 如果甲数比乙数的少5,甲数与乙数的积是12,求甲数与乙数。设 ,列出方程组是 。
6、
如果![]() ,那么3m-n+3=
。
,那么3m-n+3=
。
7、 如果x=5,y=7满足kx–2y=1那么k= 。
8、
已知方程组![]() 的x、y相等,则m=
。
的x、y相等,则m=
。
9、 二元一次方程2x+3y=9的正整数解是 。
10、在3×( )+5×( )=9的括号内分别填上一个数,使这两个数互为相反数。
11、若x![]() +y
+y![]() =-3是关于x、y的二元一次方程,则a= ,b= 。
=-3是关于x、y的二元一次方程,则a= ,b= 。
12、设有x节车厢,y吨货物,若每节装10吨,则还剩12吨未装下,若每节装12吨,则还剩下1节车厢,则所列方程组为 。
二、选择题(每题3分,共24分)
1、下列方程中,二元一次方程共有( )
①3x+6=2x ② xy=3 ③y![]() ④10x
④10x![]()
A、1个 B 、2个 C 、3个 D、 4个
2、下列各组数中,既是2x-y=3的解,又是3x+4y=10的解是( )
A、![]() B、
B、 ![]() C 、
C 、![]() D、
D、![]()
3、学校的篮球数比排球数的2倍少3个,篮球数与排球数的比是3:2,求两种球各有多少个?若设篮球x有个,排球y有个,则依题意得方程组 ( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
4、用加减法将方程组![]() 中的未知数消去后得到的方程是( )
中的未知数消去后得到的方程是( )
A、y=4 B、7y=4 C、–7y=4 D、-7y=14
5、已知方程 ① 3x-4y=10 ②3y+2x= -1 ③6y=4-5x ④2y-7=4x+1 则![]() 所满足的方程是( )
所满足的方程是( )
A、① B、①② C、①③ D、①②④
6、为了节约用水,某市规定:每户居民每月用水不超过20立方米按每立方米2元收费,超过20立方米,则超过部分按每立方米4元收费。某户居民三月份交水费72元,则该户居民三月份实际用水为( )
A、8立方米 B、18立方米 C、28立方米 D、36立方米
7、某种商品进货价便宜8﹪,而售价保持不变,那么他的利润(按进货价而定),可由目前x﹪增加到(x+10) ﹪,则x﹪是( )
A、12﹪ B、15﹪ C、30﹪ D、50﹪
8、若︱3a+b+5︱+︱2a-2b-2︱=0,则![]() -
-![]() 的值为( )
的值为( )
A、14 B、2 C、-2 D、-4
三、解答题(20分+5分+5分+6分+7分+9分)
1、用适当的方法解下列方程组(20分)
①![]() ②
②![]() ③
③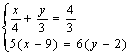
④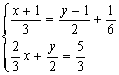 ⑤
⑤![]()
2、已知代数式![]() ,当x=-1时,它的值为-5,当x=-3时它的值是3,求p、q的值。(5分)
,当x=-1时,它的值为-5,当x=-3时它的值是3,求p、q的值。(5分)
3、如果方程组![]() 与
与![]() 的解相同,求a、b的值。(5分)
的解相同,求a、b的值。(5分)
4、在一次考试中共出了10道题,每题完全做对得10分,做错的扣6分,做对一部分得3分,李聪同学做了全部题目,得77分,问李聪同学做题情况。(6分)
5、先读懂古诗,然后回答诗中问题(7分)
巍巍古寺在林中,不知寺内几多僧,三百六十四只碗,看看用尽不差争,
三人共食一碗菜,四人共吃一碗羹,请问先生明算者,算来寺内几多僧?
6、某地生产的一种绿色蔬菜,若在市场上直接销售,每吨利润为1000元;经粗加工后销售,每吨利润可达4500元;经精加工后销售,每吨利润涨至7500元。
当地一家农工商公司收获这种蔬菜140吨。该公司加工厂的能力是:如果对蔬菜进行粗加工,每天可加工16吨;如果对蔬菜进行精加工,每天可加工6吨。但两种加工不能同时进行,受季节等条件的限制,公司必须在15天内将这批蔬菜全部销售或加工完毕。为此公司研制了三种可行方案。
方案一:将蔬菜全部进行粗加工。
方案二:尽可能多的对蔬菜进行精加工,没有来得及进行加工的蔬菜,在市场上直接销售。
方案三;将部分蔬菜进行精加工,其余蔬菜进行粗加工,并恰好15天完成。
你认为选择哪种方案获利较多?为什么? (9分)