三角形、
★★★主要知识点：
1．三角形的分类
三角形按边分类可分为_______和______(等边三角形是等腰三角形的特殊情况)；按角分类可分为______、_______和_______，
2．一般三角形的性质
(1)角与角的关系：三个内角的和等于___°；三个外角的和等于___；一个外角等于和它不相邻的两个内角之和，并且大于任何—个和它不相邻的内角，____________。
(2)边与边的关系：三角形中任两边之和大于第三边，任两边之差小于第三边。
(3)边与角的大小对应关系：在一个三角形中，__边对等角；等角对等____。
(4)三角形的主要线段的性质(见下表)：
| 名称 | 基本性质 |
| 角平分线 | ①三角形三条内角平分线相交于一点（内心）；内心到三角形三边距离相等；②角平分线上任一点到角的两边距离相等。 |
| 中线 | 三角形的三条中线相交于一点。 |
| 高 | 三角形的三条高相交于一点。 |
| 边的垂直平分线 | 三角形的三边的垂直平分线相交于一点（外心）；外心到三角形三个顶点的距离相等。 |
3. 几种特殊三角形的特殊性质
（1）等腰三角形的特殊性质：①等腰三角形的两个_____角相等；②等腰三角形_______、_____中线和______是同一条线段，三线合一；这条线段所在的直线是等腰三角形的对称轴。
（2）等边三角形的特殊性质：①等边三角形每个内角都等于___°。②三线合一
（3）直角三角形的特殊性质：①直角三角形的两个锐角互为___角； 4. 三角形的面积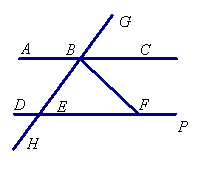
一般三角形：S △ = 
a h（ h 是a边上的高
）
例1： (基础题) 如图, AC//DF , GH是截线.
∠CBF=40°, ∠BHF=80°.
求∠HBF, ∠BFP, ∠BED.∠BEF
例2： (基础题)
①在△ABC中，已知∠B = 40°，∠C = 80°，则∠A = （度）
②：、。如图，△ABC中，∠A = 60°，∠C = 50°，则外角∠CBD = 。
③已知，在△ABC中， ∠A +
∠B = ∠C，那么△ABC的形状为（ ）
A、直角三角形
B、钝角三角形
C、锐角三角形 D、以上都不对
④下列长度的三条线段能组成三角形的是（ ）
A.3cm，4cm，8cm B.5cm，6cm，11cm C.5cm，6cm，10cm D.3cm，8cm，12cm
⑤如果一个三角形的三边长分别为x，2，3，那么x的取值范围是 。
⑥小华要从长度分别为5cm、6cm、11cm、16cm的四根小木棒中选出三根摆成一个三角形，那么他选的三根木棒的长度分别是_ ．______.
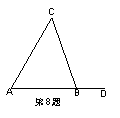
⑦已知等腰三角形的一边长为6，另一边长为10，则它的周长为
⑧在△ABC中，AB = AC，BC=10cm,∠A = 80°，则∠B = ，
∠C = 。BD=______,CD=________
⑨如图，AB = AC，BC ⊥ AD，若BC = 6，则BD = 。
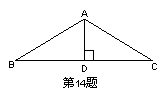
⑩画一画 如图，在△ABC中：
（1）.画出∠C的平分线CD
（2）.画出BC边上的中线AE
（3）.画出△ABC的边AC上的高BF
例3： (提高)
①△ABC中，∠C=90°，∠B-2∠A=30°，则∠A= ，∠B=
③在等腰三角形中，一个角是另一个角的2倍，求三个角？_______________________
④：在等腰三角形中，，周长为40cm,一个边另一个边2倍，求三个边？_________________
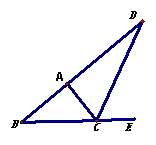例4 如图，D是△ABC的∠C的外角平分线与BA
的延长线的交点，求证：∠BAC＞∠B
例5：(15，)
例6.ABC为等边三角形，D是AC中点，E是BC延长线上一点，且CE = BC
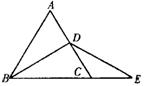求证： BD = DE
一、选择题：
1. 等腰三角形中，一个角为50°，则这个等腰三角形的顶角的度数为（ ）
A.150° B.80° C.50°或80° D.70°
2． 在△ABC中， ∠A＝50°， ∠B，∠C的角平分线相交于点O，则∠BOC的度数是( )
A． 65°
B．
115° C． 130°
D．
100°
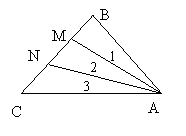
3．如图，如果∠1＝∠2＝∠3，则AM为△ 的角平分线，
AN为△ 的角平分线。
二、填空题：
1. 。
2.
3.
4. 已知△ABC中，则∠A + ∠B + ∠C = （度）
5. 。若AD是△ABC的高，则∠ADB = （度）。
6. 若AE是△ABC的中线，BC = 4，则BE = =
7. 若AF是△ABC中∠A的平分线，∠A = 70°，则∠CAF = ∠ = (度)。
8. △ABC中，BC = 12cm，BC边上的高AD = 6cm，则△ABC的面积为 。
9. 直角三角形的一锐角为60°，则另一锐角为 。
10.
等腰三角形的一个角为45°，则顶角为
。
11. 在△ABC中，∠A：∠B：∠C = 1:2:3，∠C = 。
12. 如图，∠BAC=90°，AD⊥BC，则图中共有 个直角三角形；
13. △ABC中，BO、CO分别平分∠ABC、∠ACB若∠A=70°，则∠BOC= ；若∠BOC=120°，∠A= 。
三、解答题：
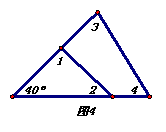
14、如图4，∠1+∠2+∠3+∠4= 度；
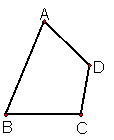
15、如图；ABCD是一个四边形木框，为了使它保持稳定的形状，需在AC或BD
上钉上一根木条，现量得AB=80㎝，BC=60㎝，
CD=40㎝，AD=50㎝，试问所需的木条长度至少要多长？
16有一天小明对同学说：“我的步子大，一步能走三米（即两脚着地时的间距有三米”。有的同学将信将疑，而小颖说：“小明，你在吹牛”。你觉得小颖的话有道理吗？
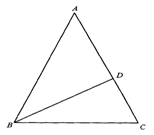
17．图1-4-27，已知在△ABC中，AB=AC，∠A=40°，
∠ABC的平分线BD交AC于D.
求：∠ADB和∠CDB的度数.
.18。已知等腰三角形的周长是25，一腰上的中线把三角形分成两个，两个三角形的周长的差是4。
求等腰三角形各边的长。
19．已知：如图，点D、E在△ABC的边BC上，AD＝AE，BD＝EC，
求证：AB＝AC
.20。.如图，已知在△ABC中，AB=AC，BD⊥AC于D，
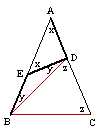CE⊥AB于E，BD与CE相交于M点。求证：BM=CM。
21．、如图，P、Q是△ABC边上的两点，且BP=PQ=QC=AP=AQ，求∠BAC的度数。
.22。如图，在△ABC中，AB=AC，点D、E分别
在AC、AB上，且BC=BD=DE=EA，求∠A的度数。
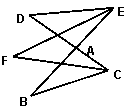23．、如图，BE、CD相交于点A，CF为∠BCD的平分线，EF为∠BED的平分线。试探求∠F与∠B、∠D之间的关系，并说明理由。
例1、填空：
。
（6）正二十边形的每个内角都等于 。
（7）一个多边形的内角和为1800°，则它的边数为 。
（8）n多边形的每一个外角是36°，则n是 。
（9）多边形的每一个内角都等于150°，则从此多边形一个顶点出发引出的对角线有 条。
（10）如果把一个多边形截去一个三角形，剩下的多边形的内角和是2160°，那么原来的多边形的边数是 。
（11）一多边形除一内角外，其余各内角之和为2570°，
则这个内角等于 。
例5、给定△ABC的三个顶点和它内部的七个点，已知这十个点中的任意三点都不在一条直线上，把原三角形分成以这些点为顶点的小三角形，并且每个小三角形的内部都不包含这十个点中的任一点，求证：这些小三角形的个数是15。