三角形、
★★★主要知识点：
1．三角形的分类
三角形按边分类可分为不等边三角形和等腰三角形(等边三角形是等腰三角形的特殊情况)；按角分类可分为锐角三角形、直角三角形和钝角三角形，其中锐角三角形、钝角三角形统称为斜角形。
2．一般三角形的性质
(1)角与角的关系：三个内角的和等于180°；一个外角等于和它不相邻的两个内角之和，并且大于任何—个和它不相邻的内角。
(2)边与边的关系：三角形中任两边之和大于第三边，任两边之差小于第三边。
(3)边与角的大小对应关系：在一个三角形中，等边对等角；等角对等边。
(4)三角形的主要线段的性质(见下表)：
| 名称 | 基本性质 |
| 角平分线 | ①三角形三条内角平分线相交于一点（内心）；内心到三角形三边距离相等；②角平分线上任一点到角的两边距离相等。 |
| 中线 | 三角形的三条中线相交于一点。 |
| 高 | 三角形的三条高相交于一点。 |
| 边的垂直平分线 | 三角形的三边的垂直平分线相交于一点（外心）；外心到三角形三个顶点的距离相等。 |
| 中位线 | 三角形的中位线平行于第三边且等于第三边的一半。 |
3. 几种特殊三角形的特殊性质
（1）等腰三角形的特殊性质：①等腰三角形的两个底角相等；②等腰三角形顶角的平分线、底边上的中线和底边上的高是同一条线段，这条线段所在的直线是等腰三角形的对称轴。
（2）等边三角形的特殊性质：①等边三角形每个内角都等于60°；②等边三角形外心、内心合一。
（3）直角三角形的特殊性质：①直角三角形的两个锐角互为余角；②直角三角形斜边上的中线等于斜边的一半；③勾股定理：直角三角形斜边的平方等于两直角边的平方和（其逆命题也成立）；④直角三角形中，30°的角所对的直角边等于斜边的一半；⑤直角三角形被斜边上的高分成的两个直角三角形和原三角形相似。
4. 三角形的面积
（1）一般三角形：S
△ = 
a h（ h 是a边上的高 )
9.多边形的内角和为 ( n – 2 )·180°（ n为边数 ）；
多边形的外角和为360°.
★★★巩固练习：
一、选择题：
1. 下列长度的三条线段能组成三角形的是（ ）
A.3cm，4cm，8cm B.5cm，6cm，11cm C.5cm，6cm，10cm D.3cm，8cm，12cm
2. 等腰三角形中，一个角为50°，则这个等腰三角形的顶角的度数为（ ）
A.150° B.80° C.50°或80° D.70°
3. 线段、等边三角形、矩形、菱形和等腰梯形这五个图形中，既是轴对称图形，又是中心对称图形的个数是（ ）
A. 2 B. 3 C. 4 D. 5
2． 在△ABC中， ∠A＝50°， ∠B，∠C的角平分线相交于点O，则∠BOC的度数是( )
A． 65°
B．
115° C． 130°
D．
100°
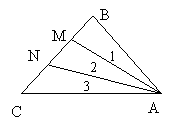3．如图，如果∠1＝∠2＝∠3，则AM为△ 的角平分线，AN为△ 的角平分线。
二、填空题：
1. 已知△ABC中，则∠A + ∠B + ∠C = （度）。
2. 在△ABC中，已知∠B = 40°，∠C = 80°，则∠A = （度）。
3. 若AD是△ABC的高，则∠ADB = （度）。
4. 若AE是△ABC的中线，BC = 4，则BE = = 。
5.
若AF是△ABC中∠A的平分线，∠A = 70°，则∠CAF = ∠ = (度)。
6. △ABC中，BC = 12cm，BC边上的高AD = 6cm，则△ABC
的面积为 。
7. 如果一个三角形的三边长分别为x，2，3，那么x的取值
范围是 。
8. 如图，△ABC中，∠A = 60°，∠C = 50°，则外角∠CBD = 。
9. 直角三角形的一锐角为60°，则另一锐角为 。
10. 
等腰三角形的一个底角为45°，则顶角为
。
11. 在△ABC中，AB = AC，∠A = 80°，则∠B = ，
∠C = 。
12. 已知等腰三角形的一边长为6，另一边长为10，则它的周长为 。
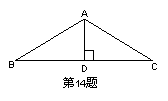
13. 如图，AB = AC，BC ⊥ AD，若BC = 6，则BD = 。
14. 在△ABC中，∠A：∠B：∠C = 1:2:3，∠C = 。
15. 内角和与外角和相等的多边形是 。
16. 在四边形ABCD中，∠A = 110°，∠B = 80°，∠C = 100°，那么∠D = 。
17. 五边形的内角和为 ，外角和为 。
18. 在四边形ABCD中，∠A：∠B：∠C：∠D = 1：2：3：4，那么∠B = 度。
19. 如果一个多边形的每个外角都等于30°，那么这个多边形是 边形。
20. n边形的内角和为1620°，则n = 。
21. 如果一个多边形的内角和等于它的外角和的3倍，那么这个多边形是 边形。
22. 小华要从长度分别为5cm、6cm、11cm、16cm的四根小木棒中选出三根摆成一个三角形，那么他选的三根木棒的长度分别是_ ．
_______.
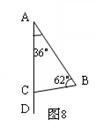
23. 如图8，在△ABC中，D是AC延长线上的一点，∠BCD= 度。
24. 在你学过的几何图形中，是轴对称图形的有______ ________（写出两个即可）。
三、解答题：
1. 已知等腰三角形的周长是25，一腰上的中线把三角形分成两个，两个三角形的周长的差是4。
求等腰三角形各边的长。
2.
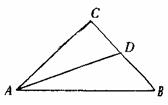如图，已知AD为等腰三角形的底角的平分线，∠C = 90°
求证：AB = AC + CD
3.
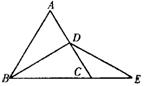
已知：如图，点D、E在△ABC的边BC上，AD＝AE，BD＝EC，
求证：AB＝AC
4.
如图，△ABC为等边三角形，D是AC中点，E是BC延长线上一点，且CE = BC
求证： BD = DE
5．画一画（每题5分，共15分）
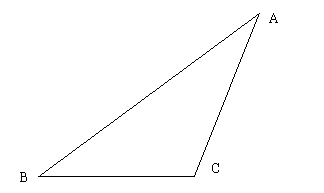如图，在△ABC中：
（1）.画出∠C的平分线CD
（2）.画出BC边上的中线AE
（3）.画出△ABC的边AC上的高BF