第八章二元一次方程组复习练习题
一、填空题
1、关于X的方程![]() ,当
,当![]() __________时,是一元一次方程; 当
__________时,是一元一次方程; 当![]() ___________时,它是二元一次方程。
___________时,它是二元一次方程。
2、已知![]() ,用
,用![]() 表示
表示![]() 的式子是___________;用
的式子是___________;用![]() 表示
表示![]() 的式子是___________。当
的式子是___________。当![]() 时
时![]() ___________;写出它的2组正整数解______________。
___________;写出它的2组正整数解______________。
3、若方程 2x![]() + y
+ y![]() =
= ![]() 是二元一次方程,则mn= 。
是二元一次方程,则mn= 。
4、已知![]() 与
与![]() 有相同的解,则
有相同的解,则![]() =
__ ,
=
__ ,![]() =
。
=
。
5、已知![]() ,那么
,那么![]() 的值是
。
的值是
。
6、 如果![]() 那么
那么![]() _______。
_______。
7、若(x—y)2+5x—7y-2=0,则x=________,y=__________ 。
8、已知y=kx+b,如果x=4时,y=15;x=7时,y=24,则k= ;b= .
9、已知![]() 是方程
是方程![]() 的一个解,则
的一个解,则![]() 。
。
10、二元一次方程4x+y=20 的正整数解是______________________。
11、从1分、2分、5分的硬币中取出5分钱,共同__________种不同的取法(不论顺序)。
12、方程组![]() 的解是_____________________。
的解是_____________________。
13、如果二元一次方程组![]() 的解是
的解是![]() ,那么a+b=_________。
,那么a+b=_________。
14、方程组![]() 的解是
的解是
15、已知6x-3y=16,并且5x+3y=6,则4x-3y的值为 。
16、若![]() 是关于
是关于![]() 、
、![]() 的方程
的方程![]() 的一个解,且
的一个解,且![]() ,则
,则![]() = 。
= 。
17、已知等腰三角形一腰上的中线将它的周长分为63和36两部分,则它的腰长是_________。底边长为___________。
18、已知点A(-y-15,-15-2x),点B(3x,9y)关于原点对称,则x的值是______,y的值是_________。
二、选择题。
1、在方程组![]() 、
、![]() 、
、![]() 、
、![]() 、
、
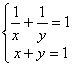 、
、![]() 中,是二元一次方程组的有( )
中,是二元一次方程组的有( )
A、2个 B、3个 C、4个 D、5个
2、
|
|
|
|
A. B. C. D.
3、三个二元一次方程2x+5y—6=0,3x—2y—9=0,y=kx—9有公共解的条件是k=( )
A.4 B.3 C.2 D.1
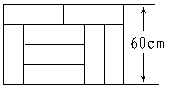
4、如图,8块相同的小长方形地砖拼成一个长方形,其中每一个小长方形的面积为( )
A. 400 cm2 B. 500 cm2 C. 600 cm2 D. 675 cm2
| |
5、一杯可乐售价1.8元,商家为了促销,顾客每买一杯可乐获一张奖券,每三张奖券可兑换一杯可乐,则每张奖券相当于( )
(A)0.6元 (B)0.5元 (C)0.45元 (D)0.3元
6、已知![]() 是方程组
是方程组![]() 的解,则
的解,则![]() 、
、![]() 间的关系是( )
间的关系是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
7、为保护生态环境,陕西省某县响应国家“退耕还林”号召,将某一部分耕地改为林地,改变后,林地面积和耕地面积共有180平方千米,耕地面积是林地面积的25%,为求改变后林地面积和耕地面积各多少平方千米。设改变后耕地面积x平方千米,林地地面积y平方千米,根据题意,列出如下四个方程组,其中正确的是( )
A![]() B
B![]() C
C![]() D
D![]()
8、设A、B两镇相距![]() 千米,甲从A镇、乙从B镇同时出发,相向而行,甲、乙行驶的速度分别为
千米,甲从A镇、乙从B镇同时出发,相向而行,甲、乙行驶的速度分别为![]() 千米/小时、
千米/小时、![]() 千米/小时,①出发后30分钟相遇;②甲到B镇后立即返回,追上乙时又经过了30分钟;③当甲追上乙时他俩离A镇还有4千米。求
千米/小时,①出发后30分钟相遇;②甲到B镇后立即返回,追上乙时又经过了30分钟;③当甲追上乙时他俩离A镇还有4千米。求![]() 、
、![]() 、
、![]() 。根据题意,由条件③,有四位同学各得到第3个方程如下,其中错误的一个是( )
。根据题意,由条件③,有四位同学各得到第3个方程如下,其中错误的一个是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
三、解答题。
1、在y=![]() 中,当
中,当![]() 时y的值是
时y的值是![]() ,
,![]() 时y的值是
时y的值是![]() ,
,![]() 时y的值是
时y的值是![]() ,求
,求![]() 的值,并求
的值,并求![]() 时y的值。
时y的值。
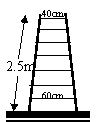
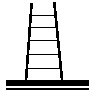
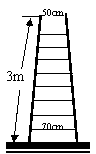 2、有三把楼梯,分别是五步梯、七步梯、九步梯,每攀沿一步阶梯上升的高度是一致的。每把楼梯的扶杆长(即梯长)、顶档宽、底档宽如图所示,并把横档与扶杆榫合处称作联结点(如点A)。
2、有三把楼梯,分别是五步梯、七步梯、九步梯,每攀沿一步阶梯上升的高度是一致的。每把楼梯的扶杆长(即梯长)、顶档宽、底档宽如图所示,并把横档与扶杆榫合处称作联结点(如点A)。
(1) ![]()
 通过计算,补充填写下表:
通过计算,补充填写下表:
| 楼梯 种类 | 两扶杆总长(米) | 横档总长(米) |
 联结点数(个) 联结点数(个) | ||||
| 五步梯 | 4 | 2.0 |
| ||||
| 七步梯 | |||||||
| 九步梯 |
(2) 一把楼梯的成本由材料费和加工费组成,假定加工费以每个个联结点1元计算,而材料费中扶杆的单价与横档的单价不相等(材料损耗及其它因素忽略不计)。现已知一把五步梯、七步梯的成本分别是26元、36元,试求出一把九步梯的成本。
3、解下列方程组
(1)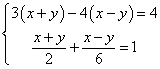 ⑵
⑵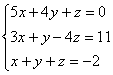
4、甲,乙联赛中,某足球队按足协的计分规则与本队奖励方案如下表.
| 胜一场 | 平一场 | 负一场 | |
| 积分 | 3 | 1 | 0 |
| 奖金(元/人) | 1500 | 700 | 0 |
当比赛进行到第12轮结束时,该队负3场,共积19分.
问:(1)该队胜,平各几场?(2)若每赛一场,每名参赛队员均得出场费500元,试求该队每名队员在12轮比赛结束后总收入。
参考答案如下:
解:(1)七步梯、九步梯的扶杆长分别是5米、6米;横档总长分别是3.5米、3.5米(各1分);联结点个数分别是14个、18个.
(2)设扶杆单价为x元/米,横档单价为y元/米。依题意得:![]()
即![]() ,解得
,解得![]() 。 故九步梯的成本为6×3+5.4×2+1×18=46.8(元) (9/).
。 故九步梯的成本为6×3+5.4×2+1×18=46.8(元) (9/).
答:一把九步梯的成本为46.8元。