7．3 实践与探究（1）
预备知识 方程组与实际问题的联系；方程组的求解．
知识要点 探索实际问题中的数量关系及方程组的应用．
1．如图，5个一样大小的小矩形拼接成一个大的矩形，如果大矩形的周长为14cm，那么小矩形的周长等于多少？
2．小红家种植水果，去年收支相抵，结余1200元．今年她家水果丰收，估计收入可比去年增加15%；而因改进了种植技术，支出可望比去年减少5%．这样今年可比去年多结余1140元．请将有关数据填入下表，再列二元一次方程组，求出小红家去年种植水果的收入、支出数．
| 项目 | 收入 | 支出 | 结余 |
| 去年 | 1200元 | ||
| 今年 |
3．阅读以下材料：
某城市出租车收费标准为：
①起步费（3千米）6.00元；
②3千米后每千米1.20元．
翁老师第一次乘了8千米，花去12.00元；第二次乘了11千米，花去15.60元．
请你利用上面的信息编制一道适当的问题，列出相应的二元一次方程组，写出求解过程．
答案：
1． 设小矩形的长、宽分别为xcm、ycm，根据图示，可列方程组
解得
即小矩形的周长为6cm
2．填表可得
| 项目 | 收入 | 支出 | 结余 |
| 去年 | x元 | y元 | 1200元 |
| 今年 | x·115%元 | y·95%元 | （1200+1140）元 |
可列方程组
解得
即去年收入6000元，支出4800元．
3．略
7．3 实践与探索（2）
预备知识 在实际问题中抽象出基本数量关系的过程．
知识要点 分析实际问题，运用方程组解决问题．
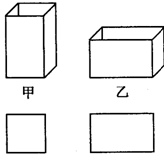
1．某纸品厂要制作如图所示的甲、乙两种无盖的长方体小盒．该厂利用边角材料裁出了长方形和正方形两种纸片，其中长方形纸片的宽与正方形纸片的边长相等．现将150张正方形纸片和300张长方形纸片，用来制作这两种小盒（不计连接部分）．试问可以做成甲、乙两种小盒各多少个？
（1）设可做成甲种小盒x个，乙种小盒y个，如何列方程组求解？
（2）设做甲种小盒要用去x张长方形纸片，做乙种小盒要用去y张长方形纸片，又如何列方程组求解？
2．北京和上海都有某种仪器可供外地使用，其中北京可提供10台，上海可提供4台．已知重庆需要8台，武汉需要6台．从北京、上海将仪器运往重庆、武汉的费用如下表所示．有关部门计划用8000元运送这些仪器，请你设计一种方案，使武汉、重庆能得到所需的仪器，而且运费正好够用．又能否修改方案，降低整个运费？
运费表 （单位：元/台）
|
起点 | 武汉 | 重庆 |
| 北京 | 400 | 800 |
| 上海 | 300 | 500 |
终点
答案：
1．（1）可列方程组
解得
即可做成甲种盒30个，乙种盒60个；
（2）可列出方程组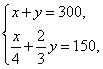
解得
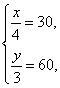
即可做成甲种盒30个，乙种盒60个
2． 设北京运往武汉x台，上海运往武汉y台，由题意，可列方程组
解得
即北京分别往武汉、重庆各运送4台、6台，上海分别往武汉、重庆各运送2台．又从运费表中，可以看出北京运往重庆的单位运费最高，考虑适当减少北京运往重庆的台数，如北京往重庆运送的台数减少为5台，此时，总运费为400×5+800×5+300+500×3=7800元，比原来降低了200元．还可以作适当调整，继续降低总运费．