第六章 平面直角坐标系
A卷•基础知识点点通
班级 姓名 得分
一、选择题（4分×6=24分）
1．点A（
）所在象限为（ ）
A、 第一象限 B、 第二象限 C、 第三象限 D、 第四象限
2．点B（
）在（）上
A、 在x轴的正半轴上 B、 在x轴的负半轴上
C、 在y轴的正半轴上 D、 在y轴的负半轴上
3．点C在x轴上方，y轴左侧，距离x轴2个单位长度，距离y轴3个单位长度，则点C的坐标为（）
A 、（
） B、 （
） C、 （
） D、（
）
4．
若点P（x,y）的坐标满足
=0，则点P 的位置是（）
A、 在x轴上 B、 在y轴上 C、 是坐标原点 D 、在x轴上或在y轴上
5．某同学的座位号为（
），那么该同学的所座位置是（）
A、 第2排第4列 B、 第4排第2列 C、 第2列第4排 D、 不好确定
6．线段AB两端点坐标分别为A（
），B（
），现将它向左平移4个单位长度，得到线段A1B1，则A1、B1的坐标分别为（）
A、
A1（
），B1（
） B 、 A1（
）， B1（0，5）
C、
A1（
） B1（-8，1） D、 A1（
） B1（
）
二、填空题（ 1分×50=50分 ）
7．分别写出数轴上点的坐标：
 |
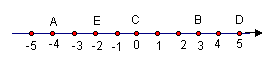A（ ） B（ ） C（ ） D（ ） E（ ）
8.在数轴上分别画出坐标如下的点：
 |
9. 点
在第 象限，点
在第 象限
点
在第 象限，点
在第
象限
点
在第 象限，点
在第
象限
10.在平面直角坐标系上，原点O的坐标是（ ），x轴上的点的坐标的特点
是 坐标为0；y轴上的点的坐标的特点是 坐标为0。
11.如图，写出表示下列各点的有序数对：
A（ ， ）； B（ ， ）； C（ ， ）； D（ ， ）；
E（ ， ）； F（ ， ）； G（ ， ）；
H（ ， ）； I（ ， ）
 | |||
 | |||
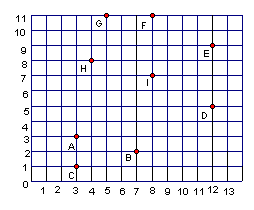12．根据点所在位置，用“+”“-”或“0”填表：
| 点的位置 | 横坐标符号 | 纵坐标符号 |
| 在第一象限 | + | + |
| 在第二象限 | ||
| 在第三象限 | ||
| 在第四象限 | ||
| 在x轴的正半轴上 | ||
| 在x轴的负半轴上 | ||
| 在y轴的正半轴上 | ||
| 在y轴的负半轴上 | ||
| 原 点 |
13．在平面直角坐标系中，将点
向右平移3个单位长度，可以得到对应点坐标（ ， ）；将点
向左平移3个单位长度可得到对应点（ ， ）；将点
向上平移3单位长度可得对应点（ ， ）；将点
向下平移3单位长度可得对应点（ ， ）。.
14．在平面内两条互相 且 的数轴，就构成了平面直角坐标系。水平的数轴称为 轴或 轴，取向 的方向为正方向；竖直的数轴称为 轴， 又称 轴， 取向 的方向为正方向；两坐标轴的交点为平面直角坐标系的
三、解下列各题（8分+8分+10分共26分）
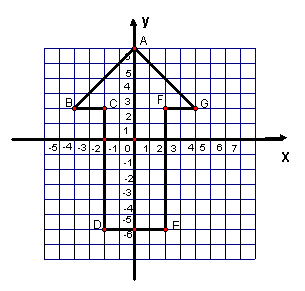15．如图，写出其中标有字母的各点的坐标，并指出它们的横坐标和纵坐标：
16．在平面直角坐标系中描出下列各点，并将各点用线段依次连接起来；
（2，1） （6，1） （6，3） （7，3） （4，6） （1，3） （2，3）
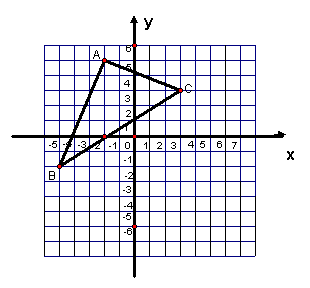17．如图，将三角形ABC向右平移2个单位长度，再向下平移3个单位长度，得到对应的三角形A1B1C1，并写出点A1、B1、C1的坐标。
附加题：（10分）
请自己动手，建立平面直角坐标系，在坐标系中描出下列各点的位置：
，
你发现这些点有什么位置关系？你能再找出类似的点吗？（再写出三点即可）