第十二章 图形的全等
★A卷1 基础知识点点通
班级 姓名 成绩
一、 选择题（3分×8＝24分）
1．全等图形是指两个图形（ ）
A、大小相同 B、形状相同 C、能够重合 D、相等
2．下面不是全等图形的性质特征的是（ ）
A、大小相同 B、形状相同 C、颜色相同 D、周长相同
3．根据下列各组的条件，能判定△ABC
△A，B，C，的是（ ）
A、AB＝A′B′，AC＝A′C′，∠C＝∠C′
B、AB＝A′B′，AC＝A′C′，∠B＝∠B′
C、AB＝A′B′，AC＝A′C′，∠A＝∠A′
D、∠A＝∠A′，∠B＝∠B′，∠C＝∠C′
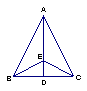4．如图，已知AB＝AC，BD
AC于D，CEAB于E，图中全等三角形的组数是（ ）
A、5 B、4 C、3 D、2
5．如图，已知AB＝AC，EB＝EC，AE的延长线交BC于D，则图中的全等三角形共有（ ）
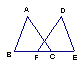A、0对 B、1对 C、2对 D、3对
6．如图，在△ABC和△DEF中，AB＝DE，∠B＝∠E，补充条件后，能直接应用“SAS”判定△ABC是△DEF的是（ ）
A、∠A＝∠D B、∠ACB＝∠DEF C、AC＝DF D、BF＝EC
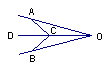
7．要测量池塘的宽度AB，画出如图所示的两个三角形，下面测出的哪组条件不能使CD＝AB（ ）
A、OA＝OD，OB＝OC B、∠B＝∠C，OB＝OC
C、∠B＝∠C，OA＝OD D、∠C＝∠B，∠A＝∠D
8．小李有两根长度分别为5㎝和8㎝的木棒，他想钉一个三角形的木框，现在有5根木棒供他选择，其长度分别为3㎝、5㎝、10㎝、13㎝、14㎝，小李可选择的木棒有（ ）
A、1种 B、2种 C、3种 D、4种
一、填空题（2分×18＝36分）
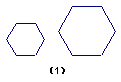
9、如图，观察下面两组图形，它们是不是全等图形
（1） （2）
（注、只需答“是”或“不是”）
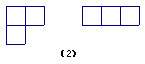
10．找出图中的全等图形是 （只写编号）
11．在下列推理中，填写需要补充的条件，使结论成立，
如图，AC＝BC，只要补充 ＝ ，
或∠ ＝∠ ，就可以证明△AOC≌△BOC。
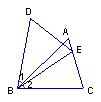
12、如图，AB＝DB，∠1＝∠2，请你添加一个适
当的条件，使△ABC≌△DBE，则需添加的条件
是
13．如图，△ABC≌△CDA，∠B＝∠D，BC＝DA，
那么：∠ACB＝ ，∠DCB＝ ，
AD∥ 。
14．如图，△ABD≌△ACE则∠EAC＝ ，
＝∠EAD。
15．如图，已知△ABC≌△DEF，AF＝5㎝，（1）求CD的长，（2）AB与DE平行吗？为什么？
解：（1）∵△ABC≌△DEF（已知）
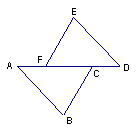∴AC＝DF（ ）
∴AC－FC＝DF－FC（等式性质）。
即 ＝ 。
∵AF＝5㎝
∴ ＝5㎝
（2）∵△ABC≌△DEF（已知），
∴∠A＝ （ ）
∴AB∥ （ ）
三、解答题（16-20每题8分）
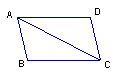
16、把图中的矩形（1）分成两个全等的三角形；（2）分成两个全等的四边形；（3）分成三个全等的四边形；（4）分成四个全等的三角形。
17、以给定的图形（○○、△△、===）为构件，构思独特且有意义的图形，举例如图，左框中是符合要求的一个图形，你还能构思出其他图形吗？请在右框中画出与之不同的一个图形，并写出一两句贴切、诙谐的解说词。
（设计合理即可，如图形有创意，解说词贴切、诙谐可另加1分）
18．如图，点A、B分别表示河两岸的两座楼房，要测得它们之间的距离，又不能够过河，还没有足够长的绳子，请你用所学过的几何知识设计一种方法，求出A、B两楼之间的距离（简要说明设计方法和理由）
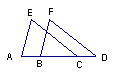19．如图、点A、B、C、D在同一条直线上，AB＝CD，EC∥FD，EC＝FD，△ACE与△BDF全等吗？请说明理由。
20、思考题：
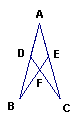现给出三个条件：（1）∠ADC＝∠AEB；（2）DC＝EB；（3）BD＝CE；请从中选择一个，填在题中的横线上，再解答。
如图，点D、E分别在AB、AC上，且AD＝AE， ，△ADC与△AEB全等吗？请说明理由。