第十二章 图形的全等
★B卷1 能力训练级级高
班级 姓名 成绩
一、选择题:(3分×6=18分)
1.下面的四组条件中,不能确定两个三角形全等的一组是( )
A、 两个三角形的两边一角对应相等
两个三角形的两边一角对应相等
B、两个三角形的两角一边对应相等
C、两个三角形的三边对应相等
D、两个三角形的两边及夹角对应相等
2.如图,已知△ABC中,AQ=PQ,PR=PS,PR![]() AB于R,PS
AB于R,PS![]() AC于S,则三个结论:
AC于S,则三个结论:
(1)AS=AR,(2)QP∥AR,(3)△BRP≌△QSR中。( )
A、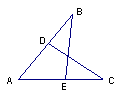 全部正确
B、仅(1)和(2)正确
全部正确
B、仅(1)和(2)正确
C、仅(1)正确 D、仅(1)和(3)正确
3.如图,D在AB上,点E在AC上,且∠B=∠C,那么补充下列一个条件后,仍无法判定△ABE≌△ACD的是( )
A。、AD=AE B、∠AEB=∠ADC C、BE=CD D、AB=AC
4.下列说法错误的是( )
A、如果两个三角形中,有一角及这个角的平分线以及这个角所对边上的高对应相等,那么这两个三角形全等
B、如果两个三角形中,有两条边和第三边上的高对应相等,那么这两个三角形全等
C、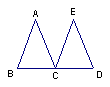 如果两个三角形中,有一边及该边上的高和中线对应相等,那么这两个三角形全等
如果两个三角形中,有一边及该边上的高和中线对应相等,那么这两个三角形全等
D、如果两个三角形中,有两个角和其中一角的平分线对应相等,那么这两个三角形全等
 5.如图,△ABC≌△ECD,∠A=48°,∠D=62°点B、C、D在同一直线上,则图中∠ACE的度数是( )
5.如图,△ABC≌△ECD,∠A=48°,∠D=62°点B、C、D在同一直线上,则图中∠ACE的度数是( )
A、38° B、48° C、132° D、62°
6.如图,△AFC≌△DEB且AF=DE,下列结论不正确的是( )
 A、∠1=∠2 B、AC=DB C、AB=DC D、∠B=∠C
A、∠1=∠2 B、AC=DB C、AB=DC D、∠B=∠C
二、选择题(3分×15=45分)
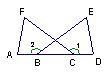
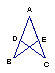 7、如图,在△ABC和△FED中,AD=FC,AB=FE当添加条件: 时,就可得到△ABC≌△FED(只需填写一个你认为正确的条件)
7、如图,在△ABC和△FED中,AD=FC,AB=FE当添加条件: 时,就可得到△ABC≌△FED(只需填写一个你认为正确的条件)
 8、如图,△AEB≌△ADC,C和B是对应顶点,∠B=25°,∠AEB=135°则∠A= °,∠C= °,∠ADC= °
8、如图,△AEB≌△ADC,C和B是对应顶点,∠B=25°,∠AEB=135°则∠A= °,∠C= °,∠ADC= °
9、已知,如图在△ABC中,AD平分∠BAC,AD![]() BC,则△ACD≌△ABD的根据是
BC,则△ACD≌△ABD的根据是

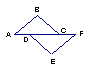
 10.已知如图,AB=EC,BF=CD要证△ABF≌△ECD,只需补充条件 =FD或AB∥EC和 ∥ 。
10.已知如图,AB=EC,BF=CD要证△ABF≌△ECD,只需补充条件 =FD或AB∥EC和 ∥ 。
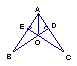
 11.如图CE
11.如图CE![]() AB于点E,BD
AB于点E,BD![]() AC于点D,BD、CE交于点O,且AO平分∠BAC,则图中的全等三角形共有 对。
AC于点D,BD、CE交于点O,且AO平分∠BAC,则图中的全等三角形共有 对。
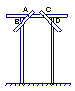
12.木工师傅在做完门框后,为防止变形,常常象如图所示那样,钉上两条斜拉的木板条(即图中的AB、CD两个木条)这样做根据的数学道理是 。

![]()
![]() 13.如图,AB=AD,AC=AE,∠BAC=∠DAE,∠B与∠D相等吗?小明的思考过程如下:
13.如图,AB=AD,AC=AE,∠BAC=∠DAE,∠B与∠D相等吗?小明的思考过程如下: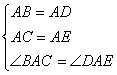 (①) △ABC≌△ADE(②)
(①) △ABC≌△ADE(②)
∠B=∠D(③)
试把每步的理由写在横线上。
(①)
(②)
(③)
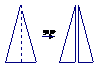 14.如图,有一腰长为5㎝,底边长为4㎝的等腰三角形纸片,沿着底边上的中线将纸片剪开,得到两个全等的直角三角形纸片,用这两个直角三角形纸片接成的平面图形中,有 个不同的四边形。
14.如图,有一腰长为5㎝,底边长为4㎝的等腰三角形纸片,沿着底边上的中线将纸片剪开,得到两个全等的直角三角形纸片,用这两个直角三角形纸片接成的平面图形中,有 个不同的四边形。
15.沿图中的虚线画线,把下面的图形划分为两个全等的图形(用二种不同方法):

三、解答题(16-19题,每题7分 20题9分)
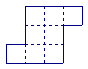
16.如图,是一块“L”形状的木板,请你用线段把它分成4个全等的部分,并且每一部分的形状仍要保持:“L”形。

 17.如图,A、B两点在一座小山的两侧,现有皮尺足够长和足够用的木杆,请你用学过的几何知识设计一种方法,求出A、B两点之间的距离(简要说明设计方法和理由)
17.如图,A、B两点在一座小山的两侧,现有皮尺足够长和足够用的木杆,请你用学过的几何知识设计一种方法,求出A、B两点之间的距离(简要说明设计方法和理由)
 18.如图,小华不小心把一块三角形玻璃打碎为三块,他能否只带其中一块碎片到商店,就能配出一块和原来一样的三角形玻璃?如果能,带哪一块去?为什么?
18.如图,小华不小心把一块三角形玻璃打碎为三块,他能否只带其中一块碎片到商店,就能配出一块和原来一样的三角形玻璃?如果能,带哪一块去?为什么?
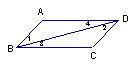 19.如图,∠1=∠2,∠3=∠4,△ABC与△DCB全等吗?为什么?
19.如图,∠1=∠2,∠3=∠4,△ABC与△DCB全等吗?为什么?
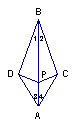 20.已知如图,∠1=∠2,∠3=∠4,点P在AB上,可以得出PC=PD吗?为什么?
20.已知如图,∠1=∠2,∠3=∠4,点P在AB上,可以得出PC=PD吗?为什么?