第十二章 图形的全等
★A卷二 基础知识点点通
班级 姓名 成绩
一、选择题（3分×8=24分）
1、下列各组所列的条件中，不能判△ABC和△DEF全等的是（ ）
A、AB=DE，∠C=∠F，∠B=∠E
B、AB=EF，∠B=∠F，∠A=∠E
C、∠B=∠E，∠A=∠F，AC=DE
D、BC=DE，AC=DF，∠C=∠D
2、下列条件中，能判定两个三角形全等的是（ ）
A、有三个角对应相等
B、有两条边对应相等
C、有两边及一角对应相等
D、有两角及一边对应相等
3、如图，要用“SAS”证△ABC≌△ADE，若已知AB=AD，AC=AE，则不需要条件（ ）
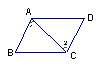A、∠1=∠2
B、BC=ED
C、∠BAC=∠DAE D、∠B=∠D
4、如图，△ABC≌△CDA，并且BC=DA，那么下列结论错误 的是（ ）
A、∠1=∠2 B、AC=CA C、AB=AD D、∠B=∠D
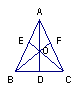
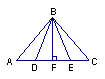
5、如图，△ABC中，AD⊥BC，AB=AC，AE=AF，则图中全等三角形的对数有（ ）
A、5对 B、6对 C、7对 D、8对
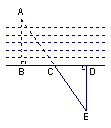
6、如图，要测量河两岸相对的两点A、B间的距离，先在过B点的AB的垂线L上取两点C、D，使CD=BC，再在过D点的垂线上取点E，使A、C、E在一条直线上，这时，△ACB≌△ECD，ED=AB，测ED的长就得AB得长，判定△ACB≌△ECD的理由是（ ）
A、SAS B、ASA C、SSS D、AAS
7、小明有两根长度分别为4㎝和9㎝的木棒，他想钉一个三角形木架，现有五根长度分别为3㎝、6㎝、11㎝、12㎝、17㎝的木棒供他选择，他有（ ）种选择
A、1
B、2 C、3
D、4
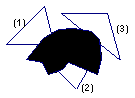
8、一块三角形玻璃样板不慎被小强同学碰破，成了四片完整四碎片（如图所示），聪明的小强经过仔细的考虑认为只要带其中的两块碎片去玻璃店就可以让师傅画一块与以前一样的玻璃样板。你认为下列四个答案中考虑最全面的是（ ）
A、带其中的任意两块去都可以 B、带1、2或2、3去就可以了
C、带1、4或3、4去就可以了 D、带1、4或2、4或3、4去均可
二、填空题（3分×15=45分）
9、已知∠ACB=∠DBC，要使△ABC≌△DCB，只需增加的一个条件是
。（只需要增加一个你认为适合的条件）
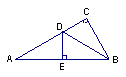
10、如图，△ABC中，∠C=90°，DB是∠ABC的平分线，点E是AB的中点，且DE⊥AB，则图中的全等三角形是
。
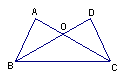
11、如图，已知AC、BD相交于点O，且AO=BO，CO=DO，则根据 可推断△AOD≌△BOC。
12、如果△ABC≌△DEF，△ABC的周长是30㎝，AB=8㎝，AC=13㎝，∠C=∠F，则EF=
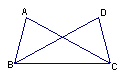
13、如图，△ABC≌△DCB，其中A和D是对应顶点，AC和DB是对应边，指出其他的对应边和对应角。对应边
，对应角
。
14、如图，已知△ABF≌△CDE，AB=CD，则BF= ，
=EC， =FC，
∠BFC= 。
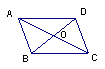
15、如图，已知AB∥CD，AD∥BC，AC交BD于点O，图中有 对三角形全等，要证明OA=OC，只需证明△ ≌△
，为此要先证明△ ≌△
。
16、如图，点D、E在△ABC上的边AC上，AD=CE，∠A=∠C，BF⊥AC于F，则图中的全等三角形共有 对。
三、解答题（17—19题，每题5分；20、21每题8分）
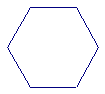
17、如图，你能把这个正六边形分成6个全等的三角形吗？能分成6个全等的四边形吗？
18、我们经常看到的人行道上由各种地砖铺砌成美丽的图案，构成图案的每一块地砖都是全等图形吗？请你自己设计一种地砖，让每一块地砖都是全等的，并且能够密铺（拼在一起没有缝隙、没有重叠）成美丽的图案。
19、小丽在一次智能大赛中，分别画了三个三角形，不料都被墨迹污染了，如图，她想分别画三个与原来完全一样的三角形，你认为是否可以，说明你的理由。
20、如图AB=DF，AC=DE，BF=CE，你能找到一对全等的三角形吗？说明你的理由。
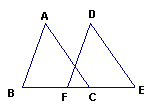
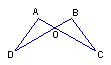
21、已知：如图，AD=AE，∠ADC=∠AEB，BE与CD相交于O点。
（1）在不添加辅助线的情况下，请写出由已知条件可得出得结论。（例如，可得出△ABE≌△ACD，∠DOB=∠EOC，∠DOE=∠BOC等）你写的结论中不得有上述所举之例，只要写出四个即可。
① ② ③ ④
（2）就你写出的其中一个结论，说明其成立的理由：
