七年级(下)数学期中试卷
一．填空：(每题2分，共20分)
1.方程－6x=48的解是 .
2．若方程
，则用含
的代数式表示
为x=
。
3.若代数式-2x5m-3y3与37x2y2n-1是同类项,则m= ,n= .
x=3
4. 已知 是方程mx+2y+2=0的解，则m= 。
y=5
5.不等式1-2x<6的负整数解有 。
6.关于x的方程x+k=2的解大于1，请写出一个符合条件的k的值 。
7. 用不等式表示“x的一半不大于3”是：
8. 一个三角形的内角中,至多有 个钝角.
9.若等腰三角形的两边长分别为3cm和4cm,则周长为 cm.
10．两条线段分别长8CM、5CM，第三条线段长CM，要使这三条线段构成一个三角形，的取值范围是
。
二.选择题(每题3分，共30分)
| 题号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 答案 |
11.若
是一元一次方程，则
A ) 1 B) 2 C) -1 D) -2 .
12.当x= 时，代数式
的值比–4小1
A ) 1 B) 2 C) -1 D) -2 .
x+2y=4
13. 方程组 的解是
x-y=1
x=4
x=2
x=1
x=-1
A) B) C) D)
y=3 y=1 y=0 y=2
14.方程x+2y=6的自然数解有 组
A ) 2 B) 3 C)4 D )5
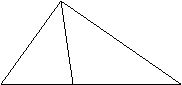
15.如图，图中共有三角形 个。
A ) 5 B) 6 C) 7 D ) 8
16.当取下列值时，能使不等式
都成立的是
A）-2.5 B)-1.5 C)0 D)1.5
17. 不等式组 
的解集是
A) 
B)
C)无解 D)
18. 若
,下列不等式成立的是
A)
B)
C)
D)
19.某班分组活动,若每组6人，则余下5人；若每组8人，则又少4人。设总人数为，组数为，则可列方程组
A） 
B） C） 
D） 
20．有20道竞赛题，对于每一题，答对得6分，答错或不答扣3分，小明在这次竞赛中的得分不少于80分，但又不多于90分，则小明答对的题数是 题
A） 14 B）15 C）16 D）17
三．解下列方程或方程组（每题5分，共10分）
21.
22. 3x-2y=12
5x+y=7
四、解答题（每题5分，共10分）。
23．当X取何值时， 代数式
.
24. 
五．解答题（25、26、27题各7分，28题9分，共30分）
25. 
如图，
中，
, B
BD平分∠ABC,求 ∠ADB的度数。
A D C
1、 26. 已知甲处干活的有31人，乙处干活的有20人，现调来18人支援，使甲处干活的人是乙处干活的人的2倍，问向甲处和乙处各分配多少人？
27. 一人上午10时以每小时6千米的速度从甲地步行到乙地，到达乙地时，已超过下午2时，但不到2点20分，求甲.乙两地的距离在什么范围内？
28．某牛奶加工厂现有鲜奶9吨，若在市场上直接销售，每吨可获取利润500元，制成酸奶销售，每吨可获利润1200元，制成奶片销售，每吨可获利润2000元，该工厂的生产能力为：如制成酸奶，每天可加工3吨，制成奶片每天可加工1吨，受人员限制，两种加工方式不能同时进行，受气温条件限制，这批牛奶必须在4天内全部销售或加工完毕，为此，该加工厂设计了两种可行性方案：
方案一：尽可能多的制成奶片，其余直接销售鲜牛奶。
方案二：将一部分制成奶片，其余制成酸奶销售，并恰好4天完成。
你认为选择哪种方案获利最多，为什么。