第二章 有理数加减测试卷⑴
班级________ 座号________姓名_______ 得分_______
一、选择题（每小题3分，共18分）
1、下面说法正确的是（ ）
A、两数之和不可能小于其中的一个加数
B、两数相加就是它们的绝对值相加
C、两个负数相加，和取负号，绝对值相减
D、不是互为相反数的两个数，相加不能得零
2、如果
，那么（ ）
A、
B、
C、
D、无法确定
的取值
3、下列等式正确的是（ ）
A、
B、
C、
D、
4、 已知
，且
，则
的值为（ ）
A、–12 B、–2 C、–2或–12 D、2
5、 已知有理数
在数轴上的位置如图，则下列结论错误的是（ ）
A、
B、
C、
D、
6、 数轴上的点A和点B所表示的数互为相反数，且点A对应的数是–2，P是到点A或点B距离为3的数轴上的点，则所有满足条件点 P所表示的数的和为（ ）.
A、0 B、6 C、10 D、16
二、填空题（每空2分，共18分）
1、用适当的数填空：（1）9.5+_____=–18； （2）_____–（+5.5）=–5.5；
（3）
； （4）
.
2、从–5中减去–1，–3，2的和，所得的差是_____.
3、利用加法的运算律，将
写成_______,可使运算简便.
4、从
与
的和中减去
所得的差是_____.
5、数轴上从左至右顺次有A、B、C三点，如果它们所表示的数的和为零，则其中示负数的点可能是点_____.
6、如果
，那么
的关系为______.
三、做一做（本题满分40分）
1、计算题：（6分）
（1）
（2）
2、计算题：（4分）
（1）
（2）
（3）
（4）
3、 请注意，大数减小数可以表示这两个数在数轴上的位置之间的距离，请找出下面几对数中距离最大的一对.
（1）6和–2 （2）7和0 （3）–1和–14 （4）9和6
4、 某港口连续4天每天的最高水位与最低水位记录如下表所示（取港口的警戒水位作为0点），哪一天水位差最大？哪一天水位差最小？
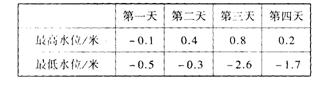
5、已个水利勘察队，第一天沿江向上游走了7千米，第二天沿江向下游走了5.3千米，第三天沿江向下游走了6.5千米，第四天沿江向上游走了10千米，第四天勘察队在出发的上游还是下游？距出发点多少千米？（6分）.
6、某地一周内每天的最高气温与最低气温记录如下表，哪天的温差最大？哪大的温差最小？（6分）.
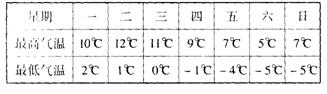
7、付自行车厂本周计划每天生产100辆自行车，由于工人实行轮休，每天上班人数不一定相等，实际每天产量与计划产量对比如下表（超出的辆数为正数，不足的辆数为负数）
（1）本周总产量与计划产量相比，增加（或减少）了多少辆？
（2）日平均产量与计划产量相比，增加（或减少）了多少辆？
四、试一试（每小题6分，共24分）
1、填空：（1）如果
，那么
（2）如果
，那么
（3）如果
，那么
2、列式并计算：
（1） 和是–2，一个加数是6，求另一个加数；
（2） 差是–5，被减数是–7，求减数；
（3） 一个数是16，另一个数比16的相反数小–2，求这两个数的差．
3、某一矿井的示意图如图2—16所示：以地面为准，A点的高度是+4米，B、C两点的高度分别是–15米与–30米．A点比B点高多少？比C点呢？
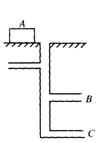
4、有一串整数–55，–54，–53，…，问：
（1）第l00个整数是什么？
（2）求这100个整数的和.
