七年级数学上学期第二章检测题
一、判断题(正确的打“√”错的打“×”)(共16分)
1.有理数分为正数和负数.( )
2.任何有理数的绝对值都是正数.( )
3.有理数都有倒数.( )
4.－x一定是负数( )
5.绝对值不大于9
的所有整数的和为0，积也为0.(
)
6.n个有理数相乘，若有奇数个负因数时，积必为负数.( )
7.－4÷
×(－4)=43.( )
8.如果一个有理数小于1，那么这个数的平方一定小于原数.( )
二、填空题(每空2分，共32分)
1.把下列各数填在相应的大括号里.
+8,+
,0.275,－｜－2｜,0,－1.04,
,－,－(－10)2,－(－8)
正整数集合｛ …｝
整数集合｛ …｝
负整数集合｛ …｝
正分数集合｛ …｝
2.－1的相反数是_____，倒数是_____，绝对值是_____.
3.一个数的平方等于
，则这个数是_____.绝对值等于
的数是_____.
4.在数轴上与点－3距离为4个单位长度的点有_____个，它们是_____.
5.已知P是数轴上的一个点，把P点向左移动3个单位后再向右移1个单位长度，这时它表示的数是－4，那么P点表示的数是_____.
6.有理数中最大的负整数是_____，绝对值最小的数是_____.
7.某地某天室内温度是18℃,室外温度是－5℃,则室内温度比室外温度高_____.
8.李斌同学利用暑假外出旅游一周，已知这一周各天的日期之和是126，那么李斌同学回家的日期是_____号.
三、选择题(将下列各题中惟一正确答案的序号填入题后括号内)(每小题3分，共15分)
1.下列说法中不正确的是( )
A.用平面去截一个正方体，能截出一个梯形
B.所有的有理数能用数轴上的点表示
C.数0是最小的整数
D.互为相反数的两个数，它们的和为零
2.已知： ①1－22;②｜1－2｜;③(1－2)2;④1－(－2),其中相等的是( )
A.②和③ B.③和④
C.②和④ D.①和②
3.若一个数的绝对值除以这个数所得的商是－1，则这个数一定是( )
A.－1 B.1或－1
C.负数 D.正数
4.用计算器计算530按键顺序正确的是( )
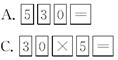
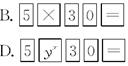
5.文具店、书店和玩具店依次座落在一条东西走向的大街上，文具店在书店西边20米处，玩具店位于书店东边100米处，小明从书店沿街向东走了40米，接着又向东走了－60米，此时，小明的位置在( )
A.文具店
B.玩具店
C.文具店西边40米
D.玩具店东边－60米
四、计算题(每小题6分，共18分)
1.(－
)2+×(－｜－2｜).
2.(－3)2÷2×(－)+4+22×(
).
3.1+2－3－4+5+6－7－8+9+10－11－12+…+97+98－99－100.
五、解答题(第1、2题各6分，3题7分，共19分)
1.把下列各数在数轴上表示出来，并且用“＞”号把它们连结起来.
－3,－(－4),0,｜－2.5｜,－1
2.下表是我国北方某城市2002年各月的平均气温表(单位:℃)
| 月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 平均气温 | －15 | －9 | －2 | 6 | 15 | 23 | 27 | 27 | 24 | 13 | －2 | －11 |
这个城市2002年全年的月平均气温是多少？
3.观察算式：
13=1
13+23=9
13+23+33=36
13+23+33+43=100
……
按规律填空：
13+23+33+43+…+103=_____.
13+23+33+…+n3=_____(n为正整数)
六、自我评价
1.解答这份试题时，你有什么收获？存在哪些方面的不足？
2.你认为这份题：A太容易；B还可以，适中；C偏难；D太难.
检测题答案或提示
一、1.× 2.× 3.× 4.× 5.√ 6.× 7.√ 8.×
二、(1)正整数集合｛+8，－(－8)，…｝
负整数集合｛－｜－2｜,－(－10)2,…｝
整数集合｛+8,－｜－2｜,0,－(－10)2,－(－8),…｝
正分数集合｛,0.275,,…｝
(2)1,－,1
(3)±,±
(4)2个，－7和1 (5)－2 (6)－1，0
(7)23℃ (8)21
三、(1)C (2)A (3)C (4)D (5)A
四、(1)－
(2)0 (3)－100
五、 1.
－(－4)＞｜－2.5｜＞0＞－1＞－3
(2)8℃
(3)552 ［
］2