第一章 走进数学世界测试题
一、填空题（每空2分，共36分）
1.一个数加7，再乘以3，然后减去12，再除以6，最后得到8，则这个数是 .
2.联欢会上，小明按4个红气球，3个黄气球，2个绿气球的顺序把气球串起来装饰会场，则第100个气球的颜色是 .
3.有两根木料，第一根长
4.某课外活动小组测得自己学校的篮球场长A米，宽B米，它的长比宽多C米，周长是D米，面积是E米，篮球架高F米.提供信息：（86，13，420，15，28，3）由于记录疏忽把数据弄乱了，你能帮他们整理一下吗？
A= ，B= ，C= ，D= ，E= .
5.用尺量一下，下面两个图形面积的大小关系是 .
6.对A，B，C有如下的计算规定：2→A→4，5→A→7，7→B→4，10→B→7，1→C→4，
3→C→12，请在横线上填上数或相应的字母:
（1）14→B→A→C→ ；（2）5→C→B→ →19；（3）40→ →A→B→36；
（4） →C→B→45.
7. 把一根绳子对折后再对折，然后在其一个三等分处剪断，这样变成了________根绳子，其中最长的是最短的长度的________倍.
8. 如果a，b是任意两个不等于零的数，定义运算+如下（其余符号意义如常）：
a+b=
，那么[(1+2) +3]－[1+(2+3)]的值是_____________.
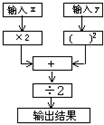
9. 右图是一个数值转换机的示意图，
若输入
的值为3，y的值为-2时，
则输出的结果为：_________________．
10. 把两个长
二、选择题（每题3分，共33分）
11. 某学生在暑假期间观察了x天的天气情况，其结果是（1）共有7天上午是晴天；（2）共有5天下午是晴天；（3）共下了8次雨；（4）下午下雨的那天，上午是晴天，则x= （ ）.
A.8 B
12.把14个棱长为1的正方体，在地面上堆叠成
如图所示的立体，然后将露出的表面部分染成红
色，那么红色部分的面积为（ ）
A．21
B．
13. 春节晚会上，电工师傅在礼堂四周挂了一圈只有绿、黄、蓝、红四种颜色的彩灯，起排列规则是：绿黄黄红蓝红红绿黄黄红蓝红红绿黄黄红蓝红红绿黄黄红蓝红红…，那么，第2006个彩灯的颜色是（ ）
A.绿色 B.黄色 C.红色 D.蓝色
14. 根据图中骰子的三种不同状态显示的数字，推出？处的数字是（ ）
A．1 B．
5
1
?
4 1 2 3 4 5
15.把10个相同的小正方体按如图的位置堆放，它的外
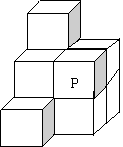表会有若干个小正方形，如果将图中标有字母P的一个
小正方体搬去，这时外表含有的小正方形的个数与搬动
前相比（ ）
A．不增不减 B．减少一个
C．减少2个 D．减少3个
16. 
个连续自然数按规律排成右表: 0 3 →
4 7 → 8 11 …
↓ ↑ ↓ ↑ ↓ ↑
1 → 2 5 → 6 9 → 10
根据规律, 从2004到2006, 箭头的方向依次应为（ ）
A.↑→ B. →↑ C.↓→ D. →↓
17. 某中学初一年级有13个课外兴趣小组，共158人。各组人数如下表：
| 组别 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 人数 | 2 | 3 | 5 | 7 | 9 | 10 | 11 | 14 | 13 | 17 | 21 | 22 | 24 |
一天下午学校同时举办语文、数学两个讲座，已知有12个小组去听讲座，其中听语文讲座的人数是听数学的6倍，还剩下一个小组在教室里讨论问题，这一小组是（ ）
A.第4组 B.第7组 C.第9组 D.第12组
18. 下面有四种说法：（1）1+2-3+4-5+6-7+8-9+10- ……-2001+2002的结果是偶数；（2）（奇数×奇数）×（奇数—奇数）=奇数；（3）2002个连续自然数的和必是偶数；（4）存在整数a、b，使（a+b）(a-b)=2002.其中正确的说法有（ ）
A．0个 B．1个 C．2个 D．3个
19. 现有A、B、C、D、E五个同学，他们分别为来自一中、二中、三中的学生，已知：（1）每所学校至少有他们中的一名学生；（2）在二中的晚会上，A、B、E作为被邀请的客人演奏了小提琴；（3）B过去曾在三中学习，后来转学了，现在同D在同一个班学习；（4）D、E是同一所学校的三好学生，根据以上叙述可以断定A所在的学校为（ ）
A．一中 B．二中 C．三中 D．不确定
20给出两列数：1，3，5，7，9，……2001和6，11，16，……，2001，同时出现在这两列数中的数的个数为（ ）
A．199 B．
21.有A、B、C三个盒子，分别装有红、黄、蓝三种颜色的小球之一种，将它们分给甲、乙、丙三个人. 已知甲没有得到A盒；乙没有得到B盒，也没有得到黄球；A盒中没有装红球，B盒中装着蓝球. 则丙得到的盒子编号与小球的颜色分别是（A ）
（A）A, 黄; (B) B，蓝; (C)C，红; (D)C，黄.
三、解答题（共31分）
22.（6分）如图，A，B，C，D，E五人围坐着圆桌，祝贺A生日.小华问他们当时的座位.
A说：“我在B的旁边.”
B说：“我的左边不是C就是D.”
C说：“我在D的旁边.”
D说：“不，C在B的右边是错的.”
只有E做了如实的回答：“除B说的正确之外，A，C，D都说错了.”
你能确定他们的位置吗？
23.（7分）如图所示，有25个点，横竖都以相等间隔排列.请想出尽可能多的方法将点连成面积不同的正方形.一共给出8个备用栏，但不一定有8个答案，请在一个备用栏里画出一个图形.
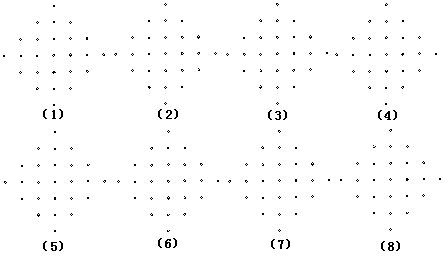
24.（8分） （1）在如图（1）所示的正方体表面展开图中三个空白正方形内各填入一个质数，使该图复原成正方体后，三组对面上两数之和都相等
（2）图（2）是由四个图（1）所示正方体拼成的长方体，其中有阴影的面上为合数，无阴影的面上为质数，且整个表面任意两个相邻正方形内的数都不是图（1）所示正方体相对面上的两数，已知长方体正面上的四个数之和为质数，那么左侧面上的数是_______（填具体数）
（3）如果把图（2）中的长方体从中间等分成左右两个小长方体，它们各自表面上的各数之和分别记为S左和S右，那么S左与S右的大小关系是S左_______S右
 |
25.（10分） 现有三包杂拌糖，由甲、乙、丙三种水果糖按不同比例混合而成. 第一包中含甲种水果糖60%和乙种水果糖40%，第二包中含乙种水果糖10%和丙种水果糖90%，第三包中含甲种水果糖20%、乙种水果糖50%和丙种水果糖30%.
先从三包中各取适量杂拌糖，重新混合，得到
（1） 试用新得到的杂拌糖中所含第一包杂拌糖的质量表示其中所含第二包杂拌糖的质量；
（2） 求新杂拌糖中所含第二包杂拌糖的质量范围.
参考答案：
5. S
=S
如图原阴影部分面积分别等于两个
边长相等的正方形的面积.
6.（1）52，（2）A （3）B （4）12
7. 5；4或2 8. —
9. 5
10. 10 三个面的面积分别是：1×2，1×3，
2×3，原长方体的表面积为2×（1×2+1×3+2×3）=22，改变之后为
2×（6×2+6×0.5+2×0.5）=32，所以增加
.
二.
11. C (由题知他们每天上、下午各测一次，七次上午晴，五次下午晴，共下八次雨，
所以共测了20次，所以是10天).
12. C（相当于涂了底层的上面和每层的侧面，则共有9+4+8+12=33）;
13.C （观察发现每七个为一个循环，而2006=7×287+4，而第四个是红色）;
14. D （由前三个发现1和2，3，4，5都相邻，所以1对的数字应是6）
15. A 16. C（观察发现每四个数字为一个循环，所以2004至2006相当与4至6）;
17.B （由题知参加数学与语文的人数应该是7的整数倍，而158减去第7组的11人正好为147人是7的整数倍，符合题意）;
18.A （1）1+2-3+4-5+6-7+8-9+10- ……-2001+2002=2003-1000=1003是奇数；
（2）（奇数×奇数）×（奇数—奇数）=偶数；
（3）2002个连续自然数的和如：
1+2+3+4+5+ ……+2001+2002中有1001个奇数和1001个偶数，其和分别为奇数和偶数，所以总和应是奇数；
（4）2002=2×7×11×13所以（a+b）和 (a-b)只能一个是奇数一个是偶数，
所以利用加减消元时
所以a不是整数）;
19. C （由已知B不在二中和三中，所以B在一中，于是D，E也在一中，而每所学校都有他们五人中的一个，所以C在二中，A在三中）
20 B （同时出现在两个数列中的数为11，21，31，41，……1991，2001共200个）
21. A
三.22.如图：有两种可能：
23. 答案：共有七种不同可能
24. 
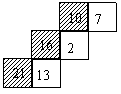（1）
（2）21 （3）＞
25. （1）设第一、二、三包分别取x千克、y千克、z千克，
则
由②得，6y+2z =3 ③.
①×2 - ③，得 2x-4y = - 1， 于是y = .
（2）由题意知，必用第二包.
如果不用第一包，即当x=0时，y有最小值为y = = ；
如果不用第三包，即当z=0时，y有最大值，此时，90%y+30%×0=1×45%，解得y = .
所以，≤ y ≤.