初二数学下期期末综合复习资料(一)
_____班 姓名__________ 学号___________ 成绩_________
一、选择题(每题2分,共36分)
1、如果![]() 是二次根式,那么
是二次根式,那么![]() 应满足的条件是(
)
应满足的条件是(
)
A、![]() ≠2的实数
B、
≠2的实数
B、![]() <2的实数
<2的实数
C、![]() >2的实数
D、
>2的实数
D、![]() >0且
>0且![]() ≠2的实数
≠2的实数
2、一个多边形的内角和与外角和相等,则这个多边形是( )
A、三角形 B、四边形 C、五边形 D、六边形
3、在![]() 、
、![]() 、
、![]() 中、
中、![]() 、
、![]() 中,最简二次根式的个数有( )
中,最简二次根式的个数有( )
A、4 B、3 C、2 D、1
4、即是轴对称图形,又是中心对称图形的是( )
A、菱形 B、等腰梯形 C、平行四边形 D、等腰三角形
5、下面结论正确的是( )
A、无限小数是无理数 B、无理数是开方开不尽的数
C、带根号的数是无理数 D、无限不循环小数是无理数
6、一个多边形的内角和与外角的和为540°,则它是( )边形。
A、5 B、4 C、3 D、不确定
7、计算![]() 的值为( )
的值为( )
A、-2 B、2 C、±2 D、![]()
8、矩形各内角的平分线能围成一个( )
A、矩形 B、菱形 C、等腰梯形 D、正方形
9、二次根式![]() 中
中![]() 的取值范围是( )
的取值范围是( )
A、![]() >-1 B、
>-1 B、![]() <-1 C、
<-1 C、![]() ≠-1
D、一切实数
≠-1
D、一切实数
10、平行四边形、矩形、菱形、正方形共有的性质是( )
A、对角线相等 B、对角线互相平分 C、对角线互相垂直 D、对角形互相垂直平分
11、计算![]() 的值是( )
的值是( )
A、![]() B、-0.14 C、
B、-0.14 C、 ![]() D、
D、 ![]()
12、矩形ABCD的两条对角线相交于点O,∠AOD=120°,AB=5cm,则矩形的对角线长是( )
A、5cm B、10cm C、![]() D、2.5cm
D、2.5cm
13、![]()
![]() 的算术平方根是( )
的算术平方根是( )
A、![]() B、
B、![]() C、
C、![]() D、±
D、±![]()
14、直角梯形的一个内角为120°,较长的腰为6cm,一底为5cm,则这个梯形的面积为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、 ![]() 或
或![]()
15、将![]() 中的根号外的因式移入根号内后为( )
中的根号外的因式移入根号内后为( )
A、![]() B、
B、 ![]() C、
C、 ![]() D、
D、 ![]()
16、下面四组二次根式中,同类二次根式是( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
17、不能判定四边形ABCD为平行四边形的题设是( )
A、AB=CD AB ∥CD B、∠A=∠C ∠B=∠D
C、AB=AD BC=CD D、AB=CD AD=BC
18、若![]() 等于( )
等于( )
A、![]() B、
B、![]() C、2
D、
C、2
D、![]()
二、填空题(每题3分,共15分)
1、一个菱形的两条对角线分别为12cm、16cm,这个菱形的边长为______;面积S=_________。
2、比较大小:![]()
3、一个多边形的每一个内角等于144°,则它是_______边形。
4、计算:![]() _________________。
_________________。
5、在实数范围内分解因式![]() =______
_______。
=______
_______。
三、计算(每题4分,共32分)
1、
![]() 2、
2、![]()
![]()
3、![]() 4、
4、![]()
5、![]() 6、
6、![]() (
(![]() <1)
<1)
7、![]() 8、
8、![]()
四、梯形ABCD中,AD∥BC,∠A=90°,∠ADC=150°,对角线BD⊥DC,若AD=8,求BC的长。(6分)


五、如图:AC是平行四边形ABCD的对角线,E、F两点在AC上,且AE=CF。求证:四边形BFDE是平行四边形(5分)
六、若![]() ,
,![]() 。求
。求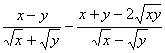 的值。(6分)
的值。(6分)
初二下期期末数学综合复习资料(二)
一、填空题:
1、![]() 的平方根是 ,
的平方根是 ,![]() =
=
![]() =
。
=
。
2、将![]() 根号外的
根号外的![]() 移入根号内是
移入根号内是
3、若![]() ,则
,则![]() 用含有
用含有![]() 的代数式表示为 。
的代数式表示为 。
4、当![]() 时,
时,![]() 在实数范围内有意义。
在实数范围内有意义。
5、已知:![]() ,则
,则![]()
6、在实数范围内分解因式:![]() 3-2
3-2![]() =
=
7、当![]() =
时,最简二次根式
=
时,最简二次根式![]() 和
和![]() 是同类二次根式。
是同类二次根式。
8、计算:![]()
![]()
9、若![]() <1,化简:
<1,化简:![]()
10、将![]() 分母有理化,其结果是
分母有理化,其结果是
二、选择题:
11、下列说法正确的是 ( )
A、![]() 的平方根是-1 B、6是
的平方根是-1 B、6是![]() 的算术平方根
的算术平方根
C、![]() 的立方根为-2 D、0.4是-0.064的立方根
的立方根为-2 D、0.4是-0.064的立方根
12、若0<![]() <1,则
<1,则![]() 、
、![]() 、
、![]() 、
、![]() 这四个数中( )
这四个数中( )
A、![]() 最大,
最大,![]() 最小
B、
最小
B、![]() 最大,
最大,![]() 最小
最小
C、![]() 最大,
最大,![]() 最小
D、
最小
D、![]() 最大,
最大,![]() 最小。
最小。
13、已知:![]() ,
,![]() ,则
,则![]() 的值是( )
的值是( )
A、 0.0140 B、 0.1410 C、 4.459 D、0.4459
14、化简二次根式![]() 的结果是( )
的结果是( )
A、 ![]() B、
B、
![]() C、
C、
![]() D、
D、![]()
15、如果![]() ,
,![]() 那么
那么![]() 、
、![]() 之间的关系是 ( )
之间的关系是 ( )
A、![]() >
>![]() B、
B、 ![]() =
=![]() C、
C、 ![]() <
<![]() D、
D、 ![]() =1
=1
16、在![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 中属于最简二次根式的个数是( )
中属于最简二次根式的个数是( )
A、 4个 B、 3个 C、 2个 D、 1个
17、若3<![]() <4,那么
<4,那么![]() 的结果是( )
的结果是( )
A、 7+2![]() B、 2
B、 2![]() -7 C、 7-2
-7 C、 7-2![]() D、 -1-2
D、 -1-2![]()
18、已知:![]() ,
,![]() ,则
,则![]() 的值为( )
的值为( )
A、 ![]() B、
B、 ![]() C、
C、 ![]() D、
D、![]()
19、如果最简根式![]() 和
和![]() 是同类根式,那么
是同类根式,那么![]() 、
、![]() 的值分别是( )
的值分别是( )
A、 ![]() =1,
=1, ![]() =1 B、
=1 B、 ![]() =1,
=1, ![]() =-1 C、
=-1 C、![]() =-1,
=-1, ![]() =1 D、
=1 D、![]() =-1,
=-1, ![]() =-1
=-1
20、下列说法中,不正确的是( )
A、![]() 有意义的条件是
有意义的条件是![]() ≥0且
≥0且![]() >0或
>0或![]() ≤0且
≤0且![]() <0
<0
B、 当![]() >1时
>1时![]() >
>![]()
C、代数式![]() 中
中![]() 的取值范围是
的取值范围是![]() ≥0且
≥0且![]() ≠1
≠1
D、分式![]() 的值为零的条件是
的值为零的条件是![]() =1
=1
三、计算与化简:
1、![]() 2、
2、![]()
3、![]() 4、
4、![]()
5、![]() 6、
6、![]()
四、已知:![]() ;
;![]() ;
;![]() ……
……
若![]() (
(![]() 、
、![]() 为正整数)请推测:
为正整数)请推测:![]() =
= ![]() =
。
=
。
五、化简求值:
(1)![]() 其中
其中![]()
(2)在直角三角形ABC,∠C=900,![]() ,
,![]() 求斜边c及面积。
求斜边c及面积。
六、解答下列各题:
1、已知:实数![]() 满足
满足![]() 求
求![]() -20002的值。
-20002的值。
2、已知![]() ,
,![]() 。求:
。求:![]() 的值。
的值。
3、若![]() 。化简:
。化简:![]()
初二下期期末数学综合复习资料(三)
一、填空题:
1、计算![]() = ;
= ;![]() ;
;![]() 。
。
2、![]() 的倒数是
。
的倒数是
。
3、当![]() 时,二次根式
时,二次根式![]() 有意义。
有意义。
4、当![]() <0时,
<0时,![]() = 。
= 。
5、在△ABC中,D、E分别是AB、AC的中点,若BC=8cm,则DE= 。
6、菱形的一个内角是60°,边长为5cm,则这个菱形较短的对角线长是 。
7、如果梯形的两底之比为2∶5,中位线长14cm,那么较大的底长为 。
8、已知线段![]() =4cm,
=4cm,![]() =9cm,线段
=9cm,线段![]() 是
是![]() 、
、![]() 的比例中项,则
的比例中项,则![]() = 。
= 。
9、已知线段![]() =2cm,
=2cm,![]() =3cm,
=3cm,![]() =6cm,
=6cm,![]() 是
是![]() 、
、![]() 、
、![]() 的第四比例项,那么
的第四比例项,那么![]() = 。
= 。
10、梯形的中位线长为6cm,上底长为4cm,那么这个梯形的下底长为 。
11、矩形ABCD的对角线AC、BD相交于点O,∠AOB=60°,AB=3.6,那么AC的长为 。
12、如图,DE∥BC且DB=AE,若AB=5,AC=10,则AE的长为 ;若BC=10,则DE的长为 。


13、如图,直角梯形ABCD的一条对角线AC将梯形分成两个三角形,△ABC是边长为10的等边三角形,则梯形ABCD的中位线EF= 。
14、矩形ABCD中,CE⊥BD,E为垂足,∠DCE∶∠ECB=3∶1,那么∠ACE= 度。
二、选择题:
1、下列图形中,不是中心对称图形的是( )
A、菱形 B、平行四边形 C、正方形 D、等腰梯形
2、如果一个多边形的内角和等于720°,那么这个多边形是( )
A、正方形 B、三角形 C、五边形 D、六边形
3、顺次连结任意四边形各边中点所得的四边形是( )
A、平行四边形 B、矩形 C、菱形 D、正方形
4、化简![]() 的结果为( )
的结果为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
5、当1<![]() <2时,化简
<2时,化简![]() 的结果是( )
的结果是( )
A、2
B、—2
C、—4
D、2![]() -4
-4
6、下列两个三角形一定相似的是( )
A、两个直角三角形 B、两个锐角三角形
C、两个等腰三角形 D、两个等边三角形
7、下列性质中,平行四边形不一定具备的是( )
A、邻角互补 B、对角互补 C、对边相等 D、对角线互相平分
8、下列命题正确的是( )
A、两条对角线相等的四边形是矩形
B、两条对角线互相垂直的四边形是菱形
C、两条对角线互相垂直平分的四边形是正方形
D、两条对角线相等的梯形是等腰梯形
9、下列二次根式中与![]() 是同类二次根式的是( )
是同类二次根式的是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
10、下列命题中真命题是( )
A、两个直角三角形是相似三角形 B、两个等边三角形是相似三角形
C、两个等腰三角形是相似三角形 D、等边三角形是中心对称图形
11、矩形具有而菱形不一定具有的性质是( )
A、对角线互相平分 B、对角线互相垂直 C、对角线相等 D、对边相等
三、解答题:
1、已知:![]() ,
,![]() 。求
。求![]() 的值。
的值。
2、已知![]() ,求
,求![]() 的值。
的值。
3、已知:如图,矩形ABCD中,E、F是AB上的两点,且AF=BE;求证:∠ADE=∠BCF



4、已知:如图,△ABC中,AB=AC,AD是BC边上的高,AE是△BAC的外角平分线,DE∥AB交AE于点E,求证:四边形ADCE是矩形。
5、已知:如图,菱形ABCD的对角线AC与BD交于点O,延长BA到点E,使AE=![]() AB,连结OE、DE,并延长DE交CA的延长线于点F;求证:OE=
AB,连结OE、DE,并延长DE交CA的延长线于点F;求证:OE=![]() DF。
DF。
6、已知:如图,在正方形ABCD中,F是CD边上的中点,点P在BC上,∠1=∠2,PE⊥BC交AC于点E,垂足为P。求证:AB=3PE。



7、如图,梯形ABCD中,AB∥CD,对角线AC、BD交于点O,∠1=∠2,AB=2BO;求证:CD=3AB
8、已知:如图,在△ABC中,∠BCA=90°,D、E分别是AC、AB的中点,点F在BC延长线上,且∠CDF=∠A;
(1)求证:四边形DECF是平行四边形;
(2)![]() ,四边形EBFD的周长为22,求DE的长。
,四边形EBFD的周长为22,求DE的长。
初二下期期末数学综合复习资料(四)
一、填空题(2×12=24分)
1、在实数范围内,当![]() 时,
时,![]() 有意义。
有意义。
2、一个多边形的内角和是1080°,这个多边形是 边形。
3、![]() 的倒数是
。
的倒数是
。
4、如果线段![]() 是线段
是线段![]() 、
、![]() 的比例中项,且
的比例中项,且![]() =1cm,
=1cm,![]() =9cm,则
=9cm,则![]() = cm。
= cm。
5、若最简二次根式![]() 与
与![]() 是同类二次根式,则
是同类二次根式,则![]() =
,
=
,![]() =
。
=
。
6、如果两个相似三角形的对应中线之比为4∶9,则它们的面积之比为 。
7、如果一个梯形的上底长为4cm,下底长为6cm,那么这个梯形的中位线长为 。
8、如果![]() ,那么
,那么![]() 。
。
9、在实数范围内分解因式![]() 。
。
10、△ABC中,DE是AC的垂直平分线,DE交AC于点E,交BC于点D,AE=3,△ABD周长为13,那么△ABC的周长为 。
11、在等腰△ABC中,AB=AC,AB=5cm,BC=8cm,那么BC边上的高为 cm。
12、如图,△ABC中,DE∥BC,若AD∶DB=1∶2,![]() =24cm2,则
=24cm2,则![]() = cm2。
= cm2。


二、选择题(2×6=12分)
1、如上图,DE∥BC,EF∥AB,则下列关系式不正确的是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
2、在![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 中,最简二次根式有( )
中,最简二次根式有( )
A、5个 B、4个 C、3个 D、2个
3、下列各组二次根式中,是同类二次根式的是( )
A、![]() 与
与![]() B、
B、![]() 与
与![]() C、
C、![]() 与
与![]() D、
D、![]() 与
与![]()
4、是中心对称图形,而不是轴对称图形的四边形是( )
A、正方形 B、矩形 C、平行四边形 D、菱形
5、若![]() -4≥3
-4≥3![]() +4,则化简
+4,则化简![]() 的结果是( )
的结果是( )
A、-4 B、4 C、2x+2 D、-2x-2
6、化简![]() 的结果是( )
的结果是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
三、计算(5×4=20分)
1、计算:![]()
2、计算:![]()
3、计算:![]()
4、已知,如图,DE∥BC,AD=2cm,BD=3cm,BC=10cm,求DE的长。



四、(6×3=18分)
1、已知:如图,在平行四边形ABCD中,∠ADE=∠CBF,点E、F在对角线AC上。求证:四边形DEBF是平行四边形。
2、已知:如图,在梯形ABCD中,AD∥BC,AB=DC,E、F分别是AB、CD边上的中点。求证:CE=BF。
3、已知:![]() ,
,![]() 。求
。求![]() 的值。
的值。
五、(6×2=12分)
1、如图,试判断顺次连结矩形ABCD四边中点所组成的四边形是什么四边形,并证明你的结论。



2、阅读下面一题的解答过程,请判断是否正确?如果不正确,请写出正确答案:
已知![]() 为实数,化简
为实数,化简![]()
解:原式=![]()
六、(8分)如图:四边形ABCD中,AB=AD,对角线AC、BD相交于点M,且AC⊥AB,BD⊥CD,过点A作AE⊥BC,垂足为E,交BD于点F。
(1)求证:MA·MC=MB·MD;
(2)AD2=BF·BD;
(3)若BE=1,AE=2,求EF的长。
七、(6分)已知:如图,在梯形ABCD中,AD∥BC,∠A=90°,AB=7,AD=2,BC=3,点P在AB上,当点P在AB上移动时,△APD与△BPC是否有相似的可能?如果有,说明此时点P在AB上的位置;如果没有,说明理由。
初二下期期末数学综合复习资料(五)
一、填空题:(每题2分;共30分)
1、4的平方根是 。
2、![]() -1的倒数是
。
-1的倒数是
。
3、已知![]() ,则
,则![]() =
。
=
。
4、当![]() 时,
时,![]() 在实数范围内有意义。
在实数范围内有意义。
5、一个多边形的内角和等于10800,则它的边数是 。
6、已知![]() 。
。
7、一个菱形的两条对角线长分别为6cm,8cm。这个菱形的面积为 cm2。
8、如果两个相似三角形对应中线的比为4∶5,那么这两个相似三角形的面积比是 。
9、如图:如果ÐAEF=ÐC,那么△AEF∽ 。


10、如图:△ABC中,DE//BC,则AD∶DB= 。
11、化简:![]() = 。
= 。
12、多项式![]() 的一次项系数为
。
的一次项系数为
。
13、如果线段![]() =2,且
=2,且![]() 、
、![]() 的比例中项为
的比例中项为![]() ,那么线段
,那么线段![]() = 。
= 。
14、梯形的上底长为3cm,下底长为5cm,则它的中位线长为 cm。
15、当![]() <2时,化简
<2时,化简![]() =
。
=
。
二、选择题:(每题3分,共24分)
1、下列运算正确的是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
2、下列说法中不正确的是( )
A、-1的立方是-1 B、-1的立方根是-1 C、![]() D、
D、![]() 是无理数
是无理数
3、下列语句正确的是( )
A、两条对角线相等的梯形是等腰梯形; B、对角线相等的四边形是矩形;
C、两条对角线垂直且相等的四边形是正方形;D、对角线互相垂直的四边形是菱形;
4、下列图形既是轴对称又是中心对称的图形是( )
A、平行四边形; B、矩形; C、等边三角形; D、等腰梯形。
5、下列说法中正确的是( )
A、无理数包括正无理数,零和负无理数; B、![]() 与
与![]() 是同类二次根式;
是同类二次根式;
C、![]() 是最简二次根式;
D、
是最简二次根式;
D、![]() 是无理数。
是无理数。
6、能判定四边形ABCD是平行四边形的题设是( )
A、AB∥CD,AD=BC; B、ÐA=ÐB,ÐC=ÐD;
C、AB=AD,ÐB=ÐD; D、AB=CD,AD=BC;
7、下列判断正确的是( )
A、△ABC和△![]() 中ÐA=400,ÐB=700,Ð
中ÐA=400,ÐB=700,Ð![]() =400,Ð
=400,Ð![]() =800则可判定两三角形相似;
=800则可判定两三角形相似;
B、有一锐角对应相等的两个直角三角形相似;
C、所有的矩形都相似;
D、所有的菱形都相似。
8、已知梯形ABCD中,AD//BC,AD=2,BC=5,E、F分别在AB和DC上,且EF//BC,![]() ,则EF的长为( )
,则EF的长为( )
A、3.5; B、3.8; C、3
D、![]() 。
。
三、解答题:
1、计算:(每小题4分,共24分)
(1)![]() (2)
(2)
![]()
(3)![]() (4)
(4)![]()
(5)解方程![]() (6)解方程
(6)解方程![]()
2、几何计算题:(10分)
(1)已知平行四边形ABCD中,AB=6cm,BC=10cm,ÐB=300。求平行四边形ABCD的面积。


(2)如图:AD是Rt△ABC斜边BC上的高,设AC=8,AB=6。求AD、BD。
四、几何证明题:(12分)
1、如图:已知△PQR为等腰三角形,且PQ=PR,Ð1=ÐA,A、Q、R、B在同一条直线上。求证:(1)△PAQ∽△BPR (4分)
(2)AQ·RB=PQ2 (3分)


2、已知P为正方形ABCD内一点,且△APD为等边三角形。若AB=2,求△APC的面积。
五、附加题:(供学有余力的同学完成)
已知: ![]() 、
、![]() 、
、![]() 为实数,
为实数,![]() ,
,![]() ,
,![]() ,那么
,那么![]() 的值是
。
的值是
。
初二下期期末数学综合复习资料(六)
一、填空题 (18×2′)
1、![]() 的算术平方根是______,-27的立方根是________。
的算术平方根是______,-27的立方根是________。
2、![]() 的整数部分是
的整数部分是![]() ,小数部分是
,小数部分是![]() ,则
,则![]() =_________。
=_________。
3、![]() ,则
,则![]() 的取值范围是_______________。
的取值范围是_______________。
4、若![]() 的取值范围是-1<
的取值范围是-1<![]() <2,则
<2,则![]() ,
,
5、方程![]() 为一元二次方程,则
为一元二次方程,则![]() =__________。
=__________。
6、方程![]() 的根为____________。
的根为____________。
7、线段![]() =2cm,
=2cm,![]() =4cm,
=4cm,![]() =10cm,则
=10cm,则![]() 、
、![]() 、
、 ![]() 的第四比例项是___________。
的第四比例项是___________。
8、已知![]() =3,
=3,![]() =12,若
=12,若![]() 是
是![]() 、
、![]() 的比例中项,则
的比例中项,则![]() =_________________。
=_________________。
9、![]() ,则
,则![]() =___ __,
=___ __,![]() =____________。
=____________。
10、若![]() ,
,![]() ,则
,则![]() =_______。
=_______。
11、如图,AA′∥BB′∥CC′,则![]() =___ __,
=___ __,![]() =___ __
=___ __
12、如图,AC平分∠BAD,请添加一个条件________________,使得![]() 。
。
13、如图,△ABC中,DE∥FG∥BC,若AD∶DF∶BF=1∶1∶1,则DE∶FG∶BC=_____________。



14、若△ABC∽△![]() 且
且![]() ,则△
,则△![]() ∽△ABC的相似比是______。若△ABC的周长为12,则△
∽△ABC的相似比是______。若△ABC的周长为12,则△![]() 的周长是______。
的周长是______。
二、选择题 ( 10×2′)
1、![]() 的结果是( )
的结果是( )
A、 ![]() B、
B、 ![]() C、
C、![]() D -
D -![]()
2、![]() 化简后的结果为(
)
化简后的结果为(
)
A、![]() B、
B、![]() C、-
C、-![]() D
D![]()
3、下列根式中,是最简二次根式的是( )
A、![]() B、
B、![]() C、
C、![]() D
D ![]()
4、最简二次根式![]() 与
与![]() 是同类二次根式,则
是同类二次根式,则![]() =( )
=( )
A、5 B、3 C、4 D、以上都不正确
5、若![]() ,则下列变形中错误的是( )
,则下列变形中错误的是( )
A、![]() B、
B、![]() C、
C、![]() D
D![]()
6、在一张比例尺是1∶500的地图上,一个图形的实际面积是625m2,则在地图上的面积为( )
A、25m2 B、25cm2 C、1.25m2 D 125m2
7、已知线段![]() 、
、![]() 、
、![]() ,作线段
,作线段![]() =
=![]() ,下列作图中若AC∥BD,则正确的是( )
,下列作图中若AC∥BD,则正确的是( )




A B C D
8、在△ABC和△![]() 中,已知AB=9cm,BC=8cm,CA=5cm,
中,已知AB=9cm,BC=8cm,CA=5cm,![]() =3cm,
=3cm,![]() =
=![]() cm ,
cm ,![]() =
=![]() cm,则(
)
cm,则(
)
A、∠A=∠A′ B、∠A=∠C′ C、∠A=∠B′ D、∠C=∠B′
9、△ABC为直角三角形,∠C=90°D为AB上一点(与A、B不重合),过D作一直线,使之截得的三角形与原三角形相似,则这样的直线有( )
A、1条 B、2条 C、3条 D、4条
10、一个等腰三角形两边长为![]() 和
和![]() ,则这个三角形的周长是( )
,则这个三角形的周长是( )
A、![]() B、
B、![]() C、
C、![]() 或
或![]() D、无法确定
D、无法确定
三、计算题 (4×4′)
1、![]() 2、
2、![]()
3、![]() 4、
4、![]()
四、解方程 (2×3′)
1、![]() (配方法)
2、
(配方法)
2、![]()
五、化简(6分)当-1<![]() <2时,化简
<2时,化简![]()
六、作图题(4分)
在方格纸中,每一个格的顶点叫做格点,以格点连线为边的三角形叫格点三角形。请在右图10×10的方格纸中,用直尺画出两个相似但不全等的格点三角形,并加以证明。要求所画三角形是钝角三角形,并标出相应字母。
七、证明与计算:
1、矩形ABCD中,AB=4,BC=6,M是BC的中点,DE⊥AM,E是垂足。①求△ABM的面积;②求DE的长;③求△ADE的面积。


2、如图:△PQR是等边三角形,∠APB=120°
(1)求证:QR2=AQ·RB
(2)若AP=![]() ,AQ=2,PB=
,AQ=2,PB=![]() 。求RQ的长和△PRB的面积。
。求RQ的长和△PRB的面积。
初二下期期末数学综合复习资料(七)
1、已知:如图,四边形ABCD是等腰梯形,AB=CD, AD∥BC, DE∥CA交BA的延长线于点E。求证:ED·AB=EA·BD


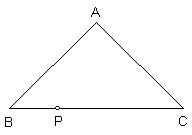
2、已知:如图,AB∥CD,AF=BF,EC=EB。求证:OC2=OF·OD
3、已知:如图, △ABC中,BC=8cm,AB=AC=5cm, 一动点P在底边上从B向C以0.25cm/秒的速度移动,当点P运动到PA与腰垂直的位置时,求P点的运动时间![]() 。
。
4、已知:如图,D为△ABC的边AC上任意一点,延长CB到E,使BE=AD,连结ED交AB于点F。求证:EF·BC=FD·AC。


5、已知梯形ABCD中,DC∥AB,在下底AB上取AE=EF,连结DE、CF并延长交于点G,AC与DG交于点M。求证: DG·ME=EG·DM。
6、已知:如图,D为△ABC内一点,连结AD、BD,以BC为边,在△ABC的形外作△BCE,使∠EBC=∠ABD,∠ECB=∠DAB。求证:∠BDE=∠BAC。


7、已知:如图,在△ABC中, ∠ACB=90°,M是BC的中点,CN⊥AM ,垂足是N。
求证:AB·BM=AM·BN。
8、如图:在大小为4×4的正方形方格中, △ABC的顶点A、B、C在单位正方形的顶点上,请在图中画一个△A1B1C1 ,使△A1B1C1∽△ABC(相似比不为1),且点A1 、B1 、C1 都在单位正方形的顶点上。


9、已知:如图,在平行四边形ABCD中,线段EF∥BC,BE、CF相交于点S,AE、DF相交于点P,求证:SP∥AB。
10、如图,在梯形ABCD中,AB∥DC,CE是∠BCD的平分线,且CE⊥AD,DE=2AE,CE把梯形分成面积为![]() 和
和![]() 两部分,若
两部分,若![]() =1,求
=1,求![]() 。
。


11、如图,菱形EFGH内接于平行四边形ABCD,并且EF∥AC∥HG, FG∥BD∥EH,AC=![]() ,BD=
,BD=![]() 。求菱形的边长。
。求菱形的边长。
12、 已知:如图:在△ABC中,D为AC的中点,在BC上截取BN=AB,连结AN交BD于E。求证: ![]() 。
。


13、如图:矩形ABCD中,AN⊥BD,N为垂足,NE⊥BC,NF⊥CD,垂足分别为E、F。求证:AN3=BD·BE·DF。
初二下期期末数学综合复习资料(八)
一、填空题:(每个2分,共30分)
1、如果![]() ,那么
,那么![]() =________。
=________。
2、如果![]() ,那么
,那么![]() =__________。
=__________。
3、线段![]() =2,
=2,![]() =3,
=3,![]() =4的第四比例项
=4的第四比例项![]() 是_________。
是_________。
4、在实数范围内分解因式:![]() =
。
=
。
5、如果![]() 的一个根为2,那么
的一个根为2,那么![]() =
。
=
。
6、一个多边形的内角和为1620°,则它的边数是 边。
7、已知在平行四边形ABCD中,∠A比∠B小50°,那么∠B= 。
8、一菱形的对角线分别为8cm与6cm,则它的面积是 cm2。
9、如图:已知矩形ABCD的对角线AC、BD相交于O,∠AOB=2∠BOC,那么∠CBO= 度。



10、如图:已知在Rt△ABC中,DC是斜边AB上的高,在这个图形中,与△ABC相似的三角形是___________ 。
11、如图:两个相同的矩形摆成“L”字形,则∠CFA=_______度。
12、已知两个相似三角形的最长边分别为25cm和10cm,较大三角形的周长为60cm,那么较小三角形的周长为 cm。
二、选择题:(每个3分,共30分)
1、下列方程中是一元二次方程的是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
2、在线段、平行四边形、正三角形、菱形、等腰梯形中,是轴对称图形的有( )
A、1个 B、2个 C、3个 D、4个
3、已知直角梯形的一腰长为20cm,这腰和底所成的角为30°,那么另一腰长是( )
A、15cm B、20cm C、10cm D、5cm
4、矩形、菱形、正方形都具有的性质是( )
A、对角线相等 B、对角线互相平分
C、对角线平分一组对角 D、对角线互相垂直
5、在四边形ABCD中,O是对角线AC、BD的交点,能判定它是平行四边形的题设是( )
A、AC=BD,AB=CD B、AD∥BC,∠A=∠C
C、AO=CO,BC=AD D、AO=CO,AB=CD
6、顺次连结菱形四边的中点,得到的四边形是( )
A、矩形 B、平行四边形 C、正方形 D、无法断定
7、如图:已知DE∥AC,则下列比例式成立的是( )
A、![]() B、
B、![]() C、
C、![]() D、以上都错
D、以上都错


8、如图:已知![]() ,∠A=63°,∠AOC=61°,则∠B=( )
,∠A=63°,∠AOC=61°,则∠B=( )
A、63° B、61° C、59° D、56°
三、解答题:(每个5分,共15分)
1、解方程:![]()
2、已知代数式![]() 的值与
的值与![]() 的值相等,试求
的值相等,试求![]() 的值;
的值;
四、解答题:(每个4分,共8分)
1、已知DE∥BC,AD∶DB=4∶3,AC=21cm, 求EC的值。


2、已知在梯形ABCD中,AD∥BC,BD⊥CD,BD平分∠ABC,且∠C=60°,CD=20,试求AD的长;
五、证明题:(每个6分,共12分)
1、在平行四边形ABCD中,AE⊥BC于E,CF⊥AD于F,求证:BE=DF。


2、在平行四边形DECF中,B是CE延长线上一点,A是CF延长线上一点,连结AB恰过点D,求证:AD·BE=DB·EC
初二下期期末数学综合复习资料(九)
一、选择题(3分×16=48分)
1、16的平方根为( )
A、4 B、-4 C、±4 D、±8
2、-27的立方根为( )
A、3 B、-3 C、±3 D、-9
3、在下列实数:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 中,无理数有(
)
中,无理数有(
)
A、1个 B、2个 C、3个 D、4个
4、如果一个多边形的内角和为360°,那么这个多边形为( )
A、三角形 B、四边形 C、五边形 D、六边形
5、下列图形中,既是轴对称图形,又是中心对称图形的是( )
A、等边三角形 B、平行四边形 C、菱形 D、等腰梯形
6、二次根式![]() 在实数范围内有意义的条件为( )
在实数范围内有意义的条件为( )
A、![]() >0
B、
>0
B、![]() <0
C、
<0
C、![]() ≥0
D、
≥0
D、![]() ≤0
≤0
7、下列计算中正确的是( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
8、若最简二次根式![]() 与
与![]() 是同类二次根式,则
是同类二次根式,则![]() 的值为(
)
的值为(
)
A、2
B、-2
C、![]() D、0
D、0
9、如果四条线段![]() 、
、![]() 、
、![]() 、
、![]() 满足等式
满足等式![]() ,那么下列各式中错误的是( )
,那么下列各式中错误的是( )
A、![]() B、
B、![]() C、
C、![]() =
=![]() D、
D、![]()
10、下列命题中,错误的是( )
A、一组邻边相等的平行四边形是菱形 B、有一个角为直角的菱形是正方形
C、一组对边平行且不相等的四边形是梯形 D、两条对角线相等的四边形是矩形
11、将![]() 分母有理化的结果为( )
分母有理化的结果为( )
A、2-![]() B、
B、![]() -2
C、-2-
-2
C、-2-![]() D、
D、![]()
12、若A、B两地的实际距离为240m,画在图上的距离![]() =4cm,则图上距离与实际距离的比为( )
=4cm,则图上距离与实际距离的比为( )
A、6000∶1 B、1∶6000 C、1∶600 D、1∶60
13、已知菱形的周长为20cm,一条对角线长为8cm,则这菱形的面积为( )
A、6cm2 B、12cm2 C、24cm2 D、48cm2
14、已知![]() ≤1,则化简
≤1,则化简![]() 的结果是( )
的结果是( )
A、-![]() -1 B、
-1 B、![]() +1 C、
+1 C、![]() -1 D、1-
-1 D、1-![]()
15、如图,平行四边形ABCD的对角线AC与BD相交于O点,在该图中全等三角形共有( )
A、一对 B、二对 C、三对 D、四对



16、如图,在梯形ABCD中,AD∥BC,∠B=80°,∠C=50°,AD=1,BC=![]() ,则AB长为( )
,则AB长为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
二、填空题(3分×4=12分)
17、在实数范围内因式分解![]() =______ ________。
=______ ________。
18、在![]() 中,已知
中,已知![]() 、
、![]() 、
、![]() ,且
,且![]() ≠0,则
≠0,则![]() =_________。
=_________。
19、如上图,在△ABC中,M、N分别是AB、AC的中点,已知△ABC的面积为8cm2,则△AMN的面积等于__________。
20、若一个梯形的中位线长为15,一条对角线把中位线分成两条线段的比是3∶2,则这梯形上、下底长分别是_________________。
三、解答题(60分)
21、(5分×4=20分)
①计算:![]() ②计算:
②计算:![]()
③化简:![]() ④已知
④已知![]() =
=![]() ,
,![]() =
=![]() ,求
,求![]() 的值
的值
22、(5分×3=15分)
(1)已知:平行四边形ABCD中,E、F分别为边AD、BC的中点,求证:EB=DF


(2)某居民小区有一块矩形空地(如上图),为美化小区,要在这块矩形空地上设计一个菱形图案,要求菱形的四个顶点分别在矩形的四条边上,且使矩形场地及其菱形组成的图案是轴对称图形。请你在右图中用尺规作出这个菱形(不写作法,保留作图痕迹)。
(3)已知:如图,EF∥BC,FD∥AB,AE=1.8cm,BE=1.2cm,CD=1.4cm,求BD的长。


23、(6分)已知:如图,正方形ABCD中,E为BD上一点,AE的延长线交CD于点F,交BC的延长线于点G,连结EC。(1)求证:△ECF∽△EGC;(2)若EF=![]() ,FG=
,FG=![]() ,求AE的长。
,求AE的长。
24、(6分)为适应西部大开发的需要,经科学论证,铁道部决定自2000年10月1日起在兰新全线(兰州至乌鲁木齐)再次提速。行驶在这一路段上的货车,将车速平均每小时提高10千米,这样提速后行驶360千米路程所用的时间与提速前行驶300千米路程所用的时间相同,问提速前后货车的速度各是多少?
25、(6分)如图,在直角△ABC中,∠C=90°,AC=4,BC=3,D为AB上的一点,AD=2。若点E在AC上,且以A、D、E为顶点的三角形与原三角形相似,试找出所有符合条件的点E,并求出AE的长。


26、(7分)如图,矩形ABCD中,CH⊥BD,垂足为H,P点是AD上的一个动点(P与A、D不重合),CP与BD交于E点。已知CH=![]() ,DH∶CD=5∶13,设AP=
,DH∶CD=5∶13,设AP=![]() ,四边形ABEP的面积为
,四边形ABEP的面积为![]() 。(1)求BD的长;(2)用含
。(1)求BD的长;(2)用含![]() 的代数式表示
的代数式表示![]() 。
。
初二下期期末数学综合复习资料(十)
一、 填空题(2×12=24分)
1、![]() 是__________的算术平方根。
是__________的算术平方根。
2、每一个外角都是720的多边形的边数是______,这个多边形的内角和等于 度。
3、已知![]() ,且
,且![]() , 则
, 则![]() ________。
________。
4、![]() 的倒数为 。
的倒数为 。
5、数轴上表示![]() 的点到原点的距离等于_____________ 。
的点到原点的距离等于_____________ 。
6、如图,在△ABC中,DE // BC,且AD=1,BD=2,则![]() ________。
________。


7、如图,平行四边形ABCD的周长为32cm,AB=6cm,对角线BD=8cm,则此平行四边形ABCD的面积为_______cm2
8、比较大小:![]() (填>或<)。
(填>或<)。
9、在Rt△ABC中,两条直角边长分别为6和8,则斜边上的中线为 。
10、一个等腰梯形的上底长为9cm,下底长为15cm,一个底角为60度,则其腰长为____cm
11、若![]() 成立,则
成立,则![]() 的取值范围是____________。
的取值范围是____________。
二、 选择题(3×6=18分)
12、一个数如果有两个平方根,那么这两个平方根的积必定( )
A、大于0 B、等于0 C、小于0 D、小于或等于0
13、下列各式计算正确的是( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
14、下面四个命题;
① 相邻的两个角都互补的四边形是平行四边形
② 对角线相等的四边形是矩形
③ 一组对边平行,另一组对边相等的四边形是平行四边形
④ 对角线互相垂直平分的四边形是菱形。
其中正确的是( )
A、①④ B、②④ C、②③ D、①③
15、如图,DE // FG // BC,且DE、FG把△ABC的面积三等份,若BC=12cm,则FG的长( )
A、6cm B、8cm
C、![]() cm
D、
cm
D、 ![]() cm
cm

16 下列叙述错误的是 ( )
A、被开方数不同的二次根式,一定不是同类二次根式;
B、同类二次根式不一定是最简二次根式;
C、判别同类二次根式,首先要把二次根式化成最简二次根式;
D、同类二次根式化成最简二次根式后被开方数一定相同;
17、在图形 ①线段;②角;③等腰三角形;④平行四边形;⑤菱形;⑥矩形中,既是轴对称图形又是中心对称图形的是( )
A、①③⑤ B、②③⑥ C、①⑤⑥ D、②④⑤
三、计算或化简(每小题4分,共20分)
18、计算![]() 19、计算
19、计算![]()
20、化简: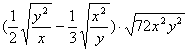 ; 21、计算:
; 21、计算:![]()
22、已知:![]() ,
,![]() 求
求![]() 的值。
的值。
四、作图题。(本题满分5分)
23、如图,已知线段AB,在AB上求作点C、D,使得AC∶CD∶DB=1∶2∶3
要求:①不写作法,保留作图痕迹
② 用一句话写明你作法的依据,并填在下面的横线上:作法的依据是
“_____________________ ___”定理
![]()
五、计算或证明:(5小题,共33分)
24、如图:△ABC中,BD、CE是两条高,AM是∠BAC的平分线,且交DE于N, 求证:![]() (6分)
(6分)


25、如图,梯形ABCD中,AD // BC,AD=3cm,BC=10cm,EF // BC交AB、DC分别于E、F,且AE=2EB。求线段EF的长(6分)
26、如图,梯形ABCD中,AD // BC,AB=DC。
(1)如果P、E、F分别是BC、AC、BD的中点,求证:AB=PE+PF
(2)如果P是BC上的任意一点(中点除外),PE // AB, PF // DC,那么AB=PE+PF这个结论还成立吗?如果成立,请证明,如果不成立,请说明理由。(7分)


27、△ABC是一块直角三角形余料,∠B=Rt∠,AB=8cm,BC=6 cm,如图将它加工成正方形零件,试说明哪种方法利用率高?(即得到的正方形面积较大)(8分)


初二下期期末数学综合复习资料(十一)
一、填空题(2×13=26分)
1、![]() 的平方根是________;
的平方根是________;![]() 的立方根是_________。
的立方根是_________。
2、已知![]() 有意义,则
有意义,则![]() 的取值范围是______________。
的取值范围是______________。
3、在![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 当中,___________________是无理数。
当中,___________________是无理数。
4、化简:![]() =_____________
=_____________
5、平方根等于![]() 和
和![]() 的数是 。
的数是 。
6、八边形的内角和等于___________度,外角和等于__________度。
7、平行四边形ABCD中,∠A∶∠B = 2∶7,则∠C=________。∠D=_______。
8、顺次连结矩形四边中点所得的四边形是_________________。
9、一个菱形的面积是24cm2,一条对角线长是6cm,则其周长是________ cm。
10、直角梯形的高和上底长都是2cm,一个底角是300,则其面积为_______________。
11、如图,平行四边形ABCD的对角线相交于点O,AD>CD,过点O作OE⊥BD交AD于E,已知△ABE的周长是![]() ,则平行四边形ABCD的周长是_________。
,则平行四边形ABCD的周长是_________。

12、设![]() ,则
,则![]() =______ 。
=______ 。
二、选择题(每小题2分,共24分)
13、一个数的平方根等于这个数本身,这个数是( )
A、 1 B、 0 C、-1 D、0或-1
14、下列说法中不正确的是( )
A、实数包括有理数和无理数 B、无理数是无限小数
C、有理数是有限小数 D、绝对值最小的实数是0
15、下列各组数的比较中,错误的是( )
A、![]() >
>![]() B、
B、![]() > 3.14 C、
> 3.14 C、![]() >
>![]() D、
D、![]()
16、下列计算正确的是( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
17、在①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 中,与
中,与![]() 是同类二次根式的是( )
是同类二次根式的是( )
A、①和③ B、②和③ C、①和④ D、③和④
18、甲、乙两同学对![]() (
(![]() >0,
>0,![]() >0)分别作了如下变形:
>0)分别作了如下变形:
甲: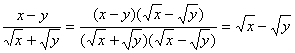
乙: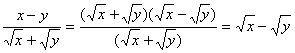
关于这两种变形过程的说法正确的是( )
A、只有甲正确 B、只有乙正确 C、甲乙都正确 D、甲乙都不正确
19、能判定一个四边形是平行四边形的条件是( )
A、一组对边平行,另一组对边相等 B、一组对边平行,一组对角相等
C、一组对边相等,一组对角相等 D、两组邻角互补
20、下列图形中是中心对称图形而不是轴对称图形的是( )
A、线段 B、平行四边形 C、矩形 D、菱形
21、如图,![]() ,另两条直线分别与其相交于点A、C、E和B、D、F,则下列式子中不一定成立的是(
)
,另两条直线分别与其相交于点A、C、E和B、D、F,则下列式子中不一定成立的是(
)
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()



22、如图,要使△ABC∽△BDC,必须具备的条件是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
23、如图,平行四边形ABCD中,E是BC的中点,F是BE的中点,AE、DF交于点H,则![]() 与
与![]() 的比值是( )
的比值是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
三、解答题:(前3题每题4分,后2题每题5分,共22分)
24、已知![]() ≈1.414,
≈1.414,![]() ≈1.732,求
≈1.732,求![]() 的值。(精确到0.01)
的值。(精确到0.01)
25、计算:![]() 26、
26、![]()
27、若![]() ,
,![]() ,求
,求![]() 的值。
的值。
28、若![]() >
>![]() >0,
>0,![]() 。求
。求![]() 的值。
的值。
四、解答或证明题(本题共28分)
29、在梯形ABCD中,AD // BC,DB⊥DC,AD=AB=DC。
(1)求∠A、∠C的度数。 (2)若AD=2cm,求它的中位线长和面积。(5分)


30、如图,过平行四边形ABCD的顶点D作直线交BC于F,交AB的延长线于E。求证:![]() (5分)
(5分)
31、如图,Rt△ABC中,∠ACB=900,D、E分别是AB、AC的中点,点F在BC的延长线上,且∠CEF=∠A。
(1)求证:DE=CF
(2)若BC=2,AB=6,求四边形DCFE的周长。
32、如图,四边形ABCD中,∠ABC=∠ADC=900,过点C作MN⊥AC分别交AB、AD的延长线于M、N,试判断∠M与∠ADB有何关系?并证明你的结论。(6分)



33、请按下列步骤折叠矩形纸片ABCD:(6分)
(1)折出折痕AC(对角线)
(2)通过折叠使AB与对角线AC重合,得折痕AG,若AB=1,BC=2,求BG的长。
初二下期期末数学综合复习资料(十二)
一、填空题(每小题2分)
1、在实数范围内因式分解:![]() =
。
=
。
2、当![]() 时,代数式
时,代数式![]() 有意义。
有意义。
3、![]() 是
的平方根。
是
的平方根。
4、若![]() =3+
=3+![]() ,则代数式
,则代数式![]() 的值是
。
的值是
。
5、比较大小:-6![]() -7
-7![]() (填“>、<或=”)
(填“>、<或=”)
6、计算:![]() =
。
=
。
7、用4米长的铁丝围成一个平行四边形,使长边与短边的比为3∶2,则长边为 米。
8、矩形ABCD中,E是边DC的中点,△AEB是等腰直角三角形,矩形ABCD的周长是24,则矩形的面积是 。
9、正方形的面积为2㎝2,则对角线的长是 。
10、在26个英文大写字母中,既是轴对称图形又是中心对称图形的个数共有 个。
11一个多边形除一个内角外,其余各内角的和等于2000°,则这个内角应等于 度。
12观察图形:图中是边长为1,2,3 …的正方形:
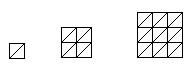
当边长![]() =1时,正方形被分成2个全等的小等腰直角三角形;
=1时,正方形被分成2个全等的小等腰直角三角形;
当边长![]() =2时,正方形被分成8个全等的小等腰直角三角形;
=2时,正方形被分成8个全等的小等腰直角三角形;
当边长![]() =3时,正方形被分成18个全等的小等腰直角三角形;……
=3时,正方形被分成18个全等的小等腰直角三角形;……
以此类推:当边长为![]() 时,正方形被分成全等的小等腰直角三角形的个数是
。
时,正方形被分成全等的小等腰直角三角形的个数是
。
二、选择题(每小题3分)
13、已知:![]() 、-
、-![]() 、
、![]() 、-3.14、
、-3.14、![]() 、0.…,其中无理数的个数有( )
、0.…,其中无理数的个数有( )
A、 2 个 B、3 个 C、 4 个 D、5个
14、下列结论中正确的是( )
A、实数分为正实数和负实数 B、没有绝对值最小的实数
C、实数![]() 的倒数是
的倒数是![]()
D、当![]() 为奇数时,实数的
为奇数时,实数的![]() 次方根有且仅有一个。
次方根有且仅有一个。
15、把![]() 根号外的因式移入根号内化简,得到的结果是( )
根号外的因式移入根号内化简,得到的结果是( )
A、![]() B、
B、![]() C、-
C、-![]() D、-
D、-![]()
16、一个直角三角形的两条边是3㎝和4㎝,则第三边长是( )
A、5㎝ B、![]() ㎝
C、5㎝或
㎝
C、5㎝或 ![]() ㎝
D、不能确定
㎝
D、不能确定
17、不等边的两个全等三角形可以拼成不同的平行四边形的个数是( )
A、2 个 B、3 个 C、4 个 D、5 个
18、下列命题正确的是( )
A、对角线相等的四边形是矩形 B、对角线垂直的四边形是菱形
C、对角线互相垂直平分的四边形是矩形 D、对角线相等的菱形是正方形
19、从平行四边形的各顶点作对角线的垂线,则顺次连结四个垂足所成的四边形是( )
A、任意四边形 B、平行四边形 C、矩形 D、菱形
20、如图,Rt△ABC中,∠BAC=90°,AD⊥BC,垂足为D,E、F分别是AB、AC的中点,∠C=30°,BC=4㎝,则四边形AEDF的周长是( )
A、4㎝ B、![]() ㎝ C、
㎝ C、![]() ㎝
D、
㎝
D、![]() ㎝
㎝

21、以线段![]() =16,
=16,![]() =13,
=13,![]() =10,
=10,![]() =6为边构造四边形,且使
=6为边构造四边形,且使![]() ∥
∥![]() ,则这样的四边形可作( )
,则这样的四边形可作( )
A、1个 B、2个 C、无数多个 D、0个
三、化简题(每题4分)
22、![]() 23、
23、![]() (
(![]() ≥0且
≥0且![]() ≠1)
≠1)
四、计算题(每题4分)
24、![]() -
-![]() +
+![]() 25、(
25、(![]() -
-![]() )2·(5+2
)2·(5+2![]() )
)
26、![]() ÷2
÷2![]() ·5
·5![]()
五、先化简,再求值(本题6分)
27、![]() 其中
其中![]()
六、(本题6分)
28、已知,一张矩形纸片ABCD的边长分别为9㎝和3㎝,把顶点A和C叠合在一起,得折痕EF(如图)
①猜想四边形AECF是什么四边形,并证明你的猜想。
②求折痕EF的长。

初二下期期末数学综合复习资料(十三)
一、填空题:
1、当![]() 时,
时,![]() 有意义;当
有意义;当![]() 时
时![]() 有意义。
有意义。
2、在△ABC中,D、E分别是AB、AC的中点,若BC=8cm,则DE= 。
3、菱形的一个内角是60°,边长为5cm,则这个菱形较短的对角线长是 。
4、如果梯形的两底之比为2∶5,中位线长14cm,那么较大的底长为 。
5、已知线段![]() =4cm,
=4cm,![]() =9cm,线段
=9cm,线段![]() 是
是![]() 、
、![]() 的比例中项,则
的比例中项,则![]() = 。
= 。
6、若实数![]() 、
、![]() 满足
满足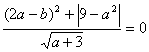 ,则
,则![]() =
=
![]() =
。
=
。
7、若 -2<![]() <2,化简
<2,化简![]() = 。
= 。
8、若![]() 是一个完全平方式,则
是一个完全平方式,则![]() 的值
。
的值
。
9、已知![]() ,则
,则![]() =
。
=
。
二、选择题:
1、化简![]() 等于( )
等于( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
2、如果![]() ,那么
,那么![]() 的值是( )
的值是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
3、下列命题中,真命题是( )
A、四边相等的四边形是正方形 B、对角线相等的菱形是正方形
C、正方形的两条对角线相等,但不互相垂直平分
D、矩形、菱形、正方形都具有“对角线相等”的性质
4、下列根式为最简二次根式的是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
5、![]() 的有理化因式是( )
的有理化因式是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
6、菱形的两条对角线长分别为6㎝和5㎝,那么这个菱形的面积为( )
A、30㎝2
B、15㎝2 C、![]() ㎝2 D、
㎝2 D、![]() ㎝2
㎝2
7、四边形ABCD是直角梯形,AD∥BC,∠B=Rt∠,∠C=300,CD长为16㎝,那么AB长为( )
A、8㎝ B、10㎝ C、16㎝ D、32㎝
8、化简![]() (
(![]() >0)等于( )
>0)等于( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
9、若0<![]() <1,则
<1,则![]() 可化简为( )
可化简为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
10、已知![]() ,则
,则![]() 的值( )
的值( )
A、1
B、3 C、![]() D、
D、![]()
三、解答题:
1、计算:![]() 2、计算:
2、计算:![]()
3、计算:![]()
4、阅读下面的解题过程,判断是否正确?如果正确,指出用了哪些运算性质,如果不正确,试简述产生错误的原因并改正。
已知:![]() <0、
<0、![]() <0,化简
<0,化简![]()
解:∵![]() <0、
<0、![]() <0
<0
∴原式=![]()
=![]()
=![]()
=![]()
初二下期期末数学综合复习资料(十四)
一、填空题:
1、当![]() _______时,
_______时,![]() 在实数范围内有意义;
在实数范围内有意义;![]() 的倒数是__________。
的倒数是__________。
2、若![]() <2,化简
<2,化简![]() =___________ ;
=___________ ;
3、化简![]() =_______________。
=_______________。
4、在实数范围内分解因式![]() =_______________________;
=_______________________;
5、![]() 与______________互为有理化因式 。
与______________互为有理化因式 。
6、比较大小:![]() ____
____![]() ,
,![]() _____
_____![]() 。
。
7、若一个多边形的内角和等于1260º,则它的边数为____ ,过一个顶点有__ __条对角线,这个多边形共有 条对角线。
8、平行四边形的周长等于40cm ,两邻边的长度之比为4∶1,则平行四边形较长的边长为______cm ;正方形的一条对角线长为![]() ,则正方形的面积为_________ 。
,则正方形的面积为_________ 。
9、如果一个矩形有一条边的长为5,对角线的长为13,则这个矩形的另一边为_______,面积为__________。
10、一个三角形的三边分别为18、10、14,和它相似的三角形的最小边是5,则最长边是__________。
11、如图:F是平行四边形ABCD中AB边的中点,E是BC边上的任意一点,![]() ,那么
,那么![]() _____ 。
_____ 。

12、梯形的上底长8cm,中位线长10cm,则下底长为__________;等腰梯形的中位线长为6cm ,腰长为5cm ,则它的周长为___________ 。
13、平行四边形ABCD的周长为48cm,对角线相交于O,△AOB的周长比△BOC的周长多4cm,则AB=________,BC=___________。
二、选择题:
1、下列各式化简正确的是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
2、若![]() 与
与![]() 互为倒数,则
互为倒数,则![]() 、
、![]() 的关系是( )
的关系是( )
A、![]() =
=![]() =1
B、
=1
B、![]() +
+![]() =1
C、
=1
C、![]() D、
D、![]() =
=![]() +1
+1
3、![]() 成立的条件是( )
成立的条件是( )
A、![]() ≥0
B、
≥0
B、![]() >2
.C、
>2
.C、![]() ≠2 D、
≠2 D、![]() ≥0
≥0
4、已知![]() <0,则
<0,则![]() 等于( )
等于( )
A、0 B、-![]() C、-2
C、-2![]() D、2
D、2![]()
5、已知一个多边形的内角和与外角和相等,那么这个多边形是( )
A、四边形 B、五边形 C、三角形 D、多边形
6、既是轴对称图形,又是中心对称图形的是( )
A、平行四边形 B、等边三角形 C、等腰梯形 D、菱形
7、如果菱形的两条对角线的长分别是6cm和8cm,则这个菱形的周长为( )
A、16cm B、20cm C、18cm D、22cm
8、边长为15cm、25cm 的一个矩形,如果一个内角的平分线分边长为两部分,则两部分的长为( )
A、12.5cm,12.5cm B、16cm,9cm C、15cm,10cm D、18 cm,7cm
9、等腰梯形的对角线互相垂直,上底为![]() ,下底为
,下底为![]() ,则这个梯形的高等于( )
,则这个梯形的高等于( )
A、![]() B、
B、![]() C、
C、![]() D、不能确定
D、不能确定
10、四边形的四边依次是![]() 、
、![]() 、
、![]() 、
、![]() ,且满足
,且满足![]() ,此四边形是( )
,此四边形是( )
A、矩形 B、菱形 C、平行四边形 D、等腰梯形
三、判断题:
1、使式子![]() 有意义,则
有意义,则![]() 的取值范围是
的取值范围是![]() ≤0( )
≤0( )
2、若![]() ,
,![]() ,则
,则![]() ( )
( )
3、![]() 、
、![]() 、
、![]() 、
、![]() 不是同类二次根式( )
不是同类二次根式( )
4、![]() ( )
( )
5、有三个角相等的四边形是矩形( )
6、两条对角线互相垂直的矩形是正方形( )
7、两条对角线垂直且相等的四边形是正方形( )
8、平行四边形的对边关于对角线交点对称( )
9、顺次连结矩形各边中点所组成的四边形是菱形( )
10、菱形的面积等于两条对角线的乘积( )
四、计算题:
①![]() ②
②![]()
③![]()
④已知![]() ,
,![]() 。求
。求![]() 的值。
的值。
五、解答题:
1、已知菱形ABCD的边长为2cm,∠BAD=1200 ,对角线AC、BD相交于O,求这个菱形的对角线长和面积。



2、如图:平行四边形ABCD中,∠A=600 ,DE平分∠ADC交BC于E,DE=3,BE=2,求平行四边形ABCD的周长和面积。
3、在等腰梯形ABCD中,,AD∥BC,对角线AC⊥AB,BD⊥CD ,∠BAD=1200,若BC=8cm,求中位线EF的长。
4、已知多边形内角和与外角和共为![]() ,求这个多边形的对角线的条数。
,求这个多边形的对角线的条数。
5、已知:如图:在ΔABC中,D是BC边上的中点,且AD=AC,DE⊥BC,DE与AB相交于点E,EC与AD相交于点F。
(1)求证:ΔABC∽ΔFCD
(2)若![]() =5,BC=10,求DE的长。
=5,BC=10,求DE的长。



六、证明题:
1、已知:如图,AD是△ABC的角平分线,DE∥AC交AB于E,DF∥AB交AC于F。求证:四边形AEDF是菱形
2、矩形ABCD中,AC、BD是对角线,过顶点C作BD的平行线与AB的延长线相交于点E。求证:△ACE是等腰三角形。
3、已知E是正方形ABCD的边BC上的中点,F是CD上一点,AE平分∠BAF。求证:AF=BC+CF


七、阅读填空题(共15分,每空3分)
阅读下面命题的证明过程后填空:
已知:如图BE、CF是ΔABC的中线,BE、CF相交于G。求证:![]()
证明:连结EF
∵E、F分别是AC、AB的中点
∴EF∥BF且EF=![]() BC
BC
∴![]()
问题:
(1)连结AG并延长AG交BC于H,点H是否为BC中点 (填“是”或“不是”)
(2)①如果M、N分别是GB、GC的中点,则四边形EFMN是 四边形。
②当![]() 的值为 时,四边形EFMN是矩形。
的值为 时,四边形EFMN是矩形。
③当![]() 的值为 时,四边形EFMN是菱形。
的值为 时,四边形EFMN是菱形。
④如果AB=AC,且AB=10,BC=16,则四边形EFMN的面积![]() = 。
= 。
参考答案或提示
(第一套)
一、CBCAD,CADDB,CBCDD,BCC
二:1、10cm,96cm2;2、<;3、10;4、1;5、![]() ;
;
三:1、45;2、![]() ;3、
;3、![]() ;4、
;4、![]() ;5、0;6、
;5、0;6、![]() ;
;
7、![]() ;8、
;8、![]() ;
;
四、BC=32
五、连结BD,可证对角线互相平分。
六、0
(第二套)
一:1、±3,±3,-![]() ;2、
;2、![]() ;3、
;3、![]() ;4、>
;4、>![]() ;5、
;5、![]() ;6、
;6、![]()
7、![]() ;8、
;8、![]() ;9、
;9、![]() ;9、1;10、
;9、1;10、![]()
二、CADBB,BBAAD
三、1、![]() ;2、3;3、
;2、3;3、![]() ;4、0;5、
;4、0;5、![]() ;6、
;6、![]()
四、![]() =8,
=8,![]() =63
=63
五、①![]() =5;②
=5;②![]() =
=![]() ,
,![]()
附加题:
1、原方程可化为![]() 解方程得:
解方程得:![]() =,故所求的值为2001。
=,故所求的值为2001。
2、原式=![]() =5
=5
3、由题意可得:![]() ≥3,
≥3,![]() <0。
<0。
当3≤![]() <4时,原式=2-
<4时,原式=2-![]() ;当
;当![]() ≥4时,原式=
≥4时,原式=![]() ;
;
(第三套)
一:1、![]() ;6、
;6、![]() ;2、
;2、![]() ;3、≥2;4、
;3、≥2;4、![]() ;5、4cm;6、5cm;7、20cm;
;5、4cm;6、5cm;7、20cm;
8、6cm;9、9cm;10、8cm;11、7.2;12、![]() ,
,![]() 。13、7.5;14、450。
。13、7.5;14、450。
二、DDACA,DBDDB,C
三:1、原式=![]()
2、原式=![]()
3、可证:△ADF≌△BCF(SAS)
4、提示:证AEDB是平行四边形得AE平行且等于BD,又因为BD=DC,所以AE平行且等于DC,故ADCE是平行四边形,又因∠ADC=Rt∠,所以ADCE是矩形。
5、菱形ABCD![]() BE∥DC
BE∥DC![]() ,又∵AB=CD,AE=
,又∵AB=CD,AE=![]() AB。∴
AB。∴![]() ∴OE是Rt△FOD斜边上的中线,∴0E=
∴OE是Rt△FOD斜边上的中线,∴0E=![]() DF。
DF。
6、∵△PCE是等腰直角三角形
∴PE=PC
由△CFP∽△BAP可得![]() ;
;
∴![]() ∴
∴![]() 即AB=3PE
即AB=3PE
7、提示;
△BAO∽△BDA![]()
梯形ABCD![]()
8、①∵EC是Rt△ABC斜边上的中线
∴EA=EC
∴∠A=∠ECA 又∵∠A=∠CDF
∴∠ECA=∠CDF
∴EC∥DF 又∵中位线ED∥BF
∴DECF是平行四边形
②设BC=![]() ,则AB=
,则AB=![]() ,BE=EC=DF=
,BE=EC=DF=![]() ,ED=CF=
,ED=CF=![]() ,由周长为22可得
,由周长为22可得![]() =2,故DE=3。
=2,故DE=3。
(第四套)
一:1、>-3;2、8;3、![]() ;4、3;5、
;4、3;5、![]() =1,
=1,![]() =0;6、16∶81;7、5cm;
=0;6、16∶81;7、5cm;
8、![]() ;9、
;9、![]() ;10、19;11、3;12、3;
;10、19;11、3;12、3;
二、BDCCBC
三:1、0;2、![]() ;3、28;4、DE=4。
;3、28;4、DE=4。
四:1、提示:可证△ADE≌△CBF得一组对边平行且相等。
2、提示:由等腰梯形的性质可证△BEC≌△CFB。
3、原式=![]()
五:1、是菱形。利用三角形的中位线定理可证明。
2、原式=![]()
六、(1)由△AMB∽△DMC可得![]()
(2)由(1)的![]()
![]() △AMD∽△BMC
△AMD∽△BMC![]() ∠ADB=∠ACB;
∠ADB=∠ACB;
又∵∠ACB=∠BAE。∴△BAF∽△BDA
(3)设EF=![]() ,由∠ABD=∠ADB=∠BAF得BF=AF=2-
,由∠ABD=∠ADB=∠BAF得BF=AF=2-![]()
在Rt△BEF中,由勾股定理得![]() ∴
∴![]()
七、设AP=![]() ,则PB=7-
,则PB=7-![]() 。当
。当![]() 或
或![]() 时,这两个三角形相似。计算得
时,这两个三角形相似。计算得![]() 或
或![]() =1或
=1或![]() =6。
=6。
(第五套)
一:1、±2;2、![]() ;3、153.6;4、≥-2;5、8;6、
;3、153.6;4、≥-2;5、8;6、![]() ;7、24;8、16∶25;
;7、24;8、16∶25;
9、△ACB;10、AE∶EC;11、![]() ;12、-3;13、7;14、4;15、1
;12、-3;13、7;14、4;15、1
二、ACABB,DBB
三、(1)计算题:
1、![]() ;2、
;2、![]() ;3、
;3、![]() ;4、
;4、![]() ;5、
;5、![]() ;6、
;6、![]() ;
;
(2)几何计算题:
1、过A作BC的垂线可求出高为3,所以面积为30。
2、∵![]()
∴![]()
∴AD=4.8
又∵![]()
∴BD=3.6
四:证明题
1、PQ=PR![]() ∠PQR=∠PRQ
∠PQR=∠PRQ![]() ∠AQP=∠BRP
∠AQP=∠BRP![]() △PAQ∽△BPR
△PAQ∽△BPR![]()
![]()
2、![]() =
=![]() +
+![]() -
-![]() =
=![]() =
=![]()
五、由![]() 可得
可得![]() ,从而
,从而![]() ;同理
;同理![]() ,
,![]() 。解方程组可得:
。解方程组可得:![]() ,
,![]() ,
,![]() 。故原式=
。故原式=![]()
(第六套)
一:1、2、-3;2、![]() ;3、
;3、![]() ≤0;4、3;5、3;6、
≤0;4、3;5、3;6、![]() ;7、5cm;8、±6;
;7、5cm;8、±6;
9、![]() 、
、![]() ;10、12;11、
;10、12;11、![]() 、
、![]() (后一空答案有多种填法)12、∠B=∠D;
(后一空答案有多种填法)12、∠B=∠D;
13、1∶2∶3;14、4∶3、16。
二、CDBAB,BACBA
三:1、![]() ;2、
;2、![]() ;3、
;3、![]() ;4、
;4、![]()
四:1、![]() ;2、
;2、![]()
五、![]()
六、略
七:
1、①![]() =6;②由△ABM∽△DEA可得
=6;②由△ABM∽△DEA可得![]() ∴DE=
∴DE=![]() ;③由
;③由![]() 得
得![]()
2、①提示:证△PAQ∽△BPR,再由PQ=PR=QR代换
②设PQ=PR=QR=![]() ,则由①知RB=
,则由①知RB=![]() ,由△PAQ∽△BPR得
,由△PAQ∽△BPR得![]() 即:
即:
![]() ∴
∴![]() ,
,![]()
(第七套)
1、由∠EAD=∠EBC=∠DCB,∠EDA=∠DAC=∠ACB=∠DBC可证△DAE∽△BCD再由AB=CD代换。
2、由∠A=∠B=∠ECB=∠D证△OCF∽△ODC
3、过A作AD⊥BC于D,由射映定理得AB2=BD·BP得BP=![]() ,∴
,∴![]() =25秒
=25秒
4、过D作DG∥AB交EC于G,
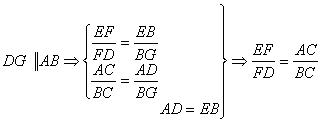
5、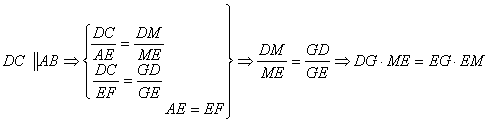
6、由已知可证△BDA∽△BEC得;![]() ,又∵∠ABC=∠DBE∴△ABC∽△DBE
,又∵∠ABC=∠DBE∴△ABC∽△DBE
7、由射影定理可知;MC2=MN·MA![]() BM2=MN·MA
BM2=MN·MA![]() △MBN∽△MAB
△MBN∽△MAB
![]()
![]()
8、略
9、AD∥EF∥BC![]()
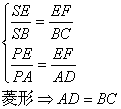
![]()
![]()
![]()
10、延长CB、DA相交于F,可证△CDE≌△CFE ∴EF=ED,![]() ,
,![]() 即
即![]() ∴
∴![]()
11、![]() ;
;![]() ,两式相加可得
,两式相加可得![]()
12、过N作NF∥BD交AC于F,则![]() ,
,![]() ,又AB=BN,AD=DC,∴
,又AB=BN,AD=DC,∴![]()
13、EN∥CD![]() ①
①
由△DFN∽△AND![]() 再加上AD=BC
再加上AD=BC![]() ②
②
由①②可得:BE·BD·DF·BC=BC·BN·AN·DN
∴BE·BD·DF=BN·AN·DN
∴BE·BD·DF=AN3。
(第八套)
一:1、-8;2、![]() ;3、6;4、
;3、6;4、![]() ;5、-3;6、11;7、1150;8、24;
;5、-3;6、11;7、1150;8、24;
9、600;10、△ACD、△BCD;11、450;12、24。
二、DDCBB,AAD
三:1、![]() ;2、
;2、![]() =1或-7;
=1或-7;
四:1、EC=9cm;2、AD=20;
五:1、证△ABE≌△CDF;
2、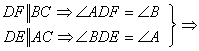 △ADF∽△DBE
△ADF∽△DBE![]()
(第九套)
一:CBCBC,ACADD,BBCDD,B
二:17、![]() ;18、
;18、![]() ;19、2cm2;20、12、18;
;19、2cm2;20、12、18;
三:21、①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]()
22、①证EBFD是平行四边形;②取矩形ABCD各边的中点,连结就得到所求的菱形。
③设EF=BD=![]() ,则
,则![]() ,
,![]() =2.1cm。
=2.1cm。
23、①证△BAE≌△BCE得:∠BAE=∠BCE=∠G=∠ECF,再加上条件公共角。
②由△ECF∽△EGC得EC2=EF·EG=6![]() AE=EC=
AE=EC=![]()
24、设提速前的速度是![]() 千米/小时,则
千米/小时,则![]() ,
,![]() =50。
=50。
∴提速前的速度是50千米/小时,提速后的速度是60千米/小时。
25、当DE∥BC时,△ADE∽△ABC,此时AE=![]() ;当△ADE∽△ACB时,AE=2.5;
;当△ADE∽△ACB时,AE=2.5;
26、①由射影定理可求出DC=5,BC=12,BD=13;②……
(第十套)
一:1、![]() ;2、5、5400;3、6;4、
;2、5、5400;3、6;4、![]() ;5、
;5、![]() ;6、
;6、![]() ;7、48;8、<;
;7、48;8、<;
9、5;10、6;11、![]() ≥2
≥2
二、CCADA,C
三:18、![]() ;19、
;19、![]() ;20、
;20、![]() ;21、-1;22、39
;21、-1;22、39
四:23、平行线分线段成比例定理
五:24、△AEC∽△ADB![]() AE·AB=AD·AC
AE·AB=AD·AC![]() △ADE∽△ABC
△ADE∽△ABC![]()
![]() △ADN∽△ABM
△ADN∽△ABM![]()
△ADE∽△ABC![]()
25、延长BA、CD相交于点G,设EB=k,
AD∥BC![]()
![]()
AD∥EF![]()
![]()
26、①由三角形中位线定理可知PE=![]() AB,PF=
AB,PF=![]() DC,又∵AB=DC ∴AB=PE+PF
DC,又∵AB=DC ∴AB=PE+PF
②成立。
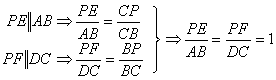 ;又∵AB=DC ∴AB=PE+PF
;又∵AB=DC ∴AB=PE+PF
27、设正方形的边长为![]() cm。
cm。
(1)如图1,FE∥BC![]()
(2)如图2,MQ∥AC![]() △BMQ∽△BCA
△BMQ∽△BCA ![]()
∵![]() <
<![]() ∴方案二利用率高。
∴方案二利用率高。
(第十一套)
一:1、±3、![]() ;2、
;2、![]() ≥
≥![]() ;3、
;3、![]() 、
、![]() ;4、
;4、![]() ;5、49提示:
;5、49提示:![]() ;6、10800、3600;7、400、1400;8、菱形;9、20
;6、10800、3600;7、400、1400;8、菱形;9、20
10、![]() cm2;11、
cm2;11、![]() ;12、1或-2。
;12、1或-2。
二、BCDDC,CBBDC,D
三:24、1.28;25、![]() ;26、
;26、![]() ;
;
27、原式=![]() =
=![]() =
=![]() ; 28、
; 28、![]() 。
。
四:29、①∠A=1200、∠C=600;②中位线长3cm、面积![]() cm2。
cm2。
30、平行四边形ABCD![]()
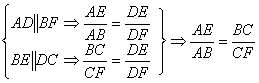 ;又因为BC=AD
;又因为BC=AD
∴![]()
31、①证△ADE≌△EFC(ASA);
②利用三角形中位线定理和勾股定理可求出周长为8。
32、答:相等。
∵CB是Rt△ACM斜边上的高
∴AC2=AB·AM 同理AC2=AD·AN
∴AB·AM=AD·AN
∴△ABD∽△ANM
∴∠M=∠ADB
33、过D作DE⊥AC于E,可证△ABG≌△AEG得:AB=AE=1,BG=GE=![]()
在Rt△EGC中,∵EG2 +EC2=GC2 ∴![]()
∴![]()
(第十二套)
一:1、![]() ;2、>1;3、6;4、-6;5、<;6、
;2、>1;3、6;4、-6;5、<;6、![]() ;
;
7、![]() ;8、128;9、2cm;10、6个;11、1600;12、
;8、128;9、2cm;10、6个;11、1600;12、![]()
二、BDCCB,DBDD
三:22、![]() ;23、
;23、![]() ;
;
四:24、![]() ;25、1;26、
;25、1;26、![]()
五、27、原式=![]() =5
=5
六:28、①连结AC交EF于点O,由题意知EF垂直平分AC,可证△EOC≌△FOA得OE=OF
∴AECF是菱形(对角线互相垂直平分)
②设OE=OF=![]() ,由△AOF∽△ABC得:
,由△AOF∽△ABC得:![]() ,即
,即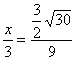
∴![]() =
=![]() ,∴EF=
,∴EF=![]()
(第十三套)
一:1、![]() <
<![]() 、
、![]() <-1;2、4cm;3、5cm;4、20cm;5、6cm;6、3、6;
<-1;2、4cm;3、5cm;4、20cm;5、6cm;6、3、6;
7、-1;8、2或6;9、±4
二、DABAB,BACAA
三;1、![]() ;2、
;2、![]() ;3、
;3、![]()
四、不正确 ∵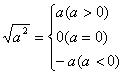 正确的解答如下:
正确的解答如下:
原式=![]()
=![]()
(第十四套)
一:1、![]() <0、
<0、![]() ;2、
;2、![]() ;3、
;3、![]() ;4、
;4、![]() ;
;
5、![]() ;6、<、<;7、9、6、27;8、16、
;6、<、<;7、9、6、27;8、16、![]() ;9、12;60;10、9;
;9、12;60;10、9;
11、4;12、12cm、22cm;13、14cm、10cm
二、CDBCA,DBAC
三、×√×√×√×√√×
四、①![]() ;②
;②![]() ;③28;④原式=
;③28;④原式=![]() =5.5
=5.5
五:1、AC=2cm;BD=![]() cm;
cm;![]() =
=![]() cm2;
cm2;
2、∵△DEC是等边三角形
∴周长是16;面积是![]() (高为
(高为![]() )
)
3、中位线EF=6cm。
4、设这个多边形是![]() 边形,则
边形,则![]() ,
,![]() =12
=12
∴这个多边形共有对角线![]() =54条。
=54条。
5、①∵AD=AC![]() ∠ACB=∠CDF;DE垂直平分BC
∠ACB=∠CDF;DE垂直平分BC![]() EB=EC
EB=EC![]() ∠B=∠ECB;
∠B=∠ECB;
∴△ABC∽△FCD
②过A作AG⊥BC于G, ∵![]() ∴
∴![]() =20,△ABC的高AG=4
=20,△ABC的高AG=4
由![]() 得;
得;![]() ∴ED=
∴ED=![]()
六:1、证AEDF是一组邻边相等平行四边形。
2、矩形ABCD![]() AC=BD;平行四边形BECD
AC=BD;平行四边形BECD![]() BD=EC ∴ AC=EC
BD=EC ∴ AC=EC
3、过E作EG⊥AF于G,证△EGF≌△ECF(HL)
七、(1)是;(2)①平行;②1;③![]() ;④16。
;④16。