2.3 相反数
一、基础训练:
1．下列说法正确的是（ ）
A．符号不同的两个数互为相反数
B．互为相反数的两个数必然一个是正数；另一个是负数
C．
的相反数是-3.14
D．0.5的相反数是-
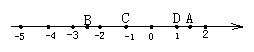
2．如图下列各点中，表示互为相反数的一对点是（ ）
A．A点和B点 B．C点和D点 C．B点和C点 D．A点和D点
3．（1）如果-x=2，则x=______；如果x=-3.5，则-x=______．
（2）a-b的相反数是______；2x+y-z的相反数是_________．
（3）若a+=0，则a=______．
4．若
A．-4 B．
5．如果a+b=0，那么下面的说法正确的是（ ）
A．a与b一定相等 B．a与b互为相反数
C．a，b互为倒数 D．a与-b互为相反数
6．若a与
互为相反数，则
A．-1 B．
7．化简下列各数．
（1）-（+2）； （2）+（+7.2）； （3）-[-（+3）]； （4）-[-（-2）]．
8．写出下列各数的相反数：
（1）-（+
）； （2）-[-（2003）]；（3）4.25的相反数；（4）-（a+1）．
二、递进演练：
1． -3的相反数是（ ）
A．
B． C．-
D．-3
2．下列四种说法中正确的是（ ）
A．
的相反数是-0．25 B．4的相反数是-
C．的相反数是-4 D．-4的相反数是-
3．写出下列各数的相反数．
（1）-（+） （2）-[-（-2002）] （3）的相反数 （4）a-b
4．下列说法中正确的是（ ）
A．的相反数是-3.14； B．符号不同的两个数一定是互为相反数
C．若x和y互为相反数，则x+y=0； D．一个数的相反数一定是负数
5．下列各数中互为相反数的是（ ），相等的是（ ）
A．-6与-（+6） B．-（-7）与+（-7）
C．-（+2）与+2．2 D．-与-（-
）
6．下列说法：①-3是相反数；②-3和+3都是相反数；③-3是+3的相反数；④-3和+3互为相反数；⑤+3与-3的相反数；⑥一个数的相反数必定是另外一个数，其中正确的有（ ）
A．2个 B．4个 C．5个 D．3个
7．在数轴上表示出下列各数和它们的相反数，并把这些数和它们的相反数用“<”号连接起来：2.5， 3.5， 4， -2
8．如图，数轴上点M所表示的数的相反数为（ ）
A．2.5 B．
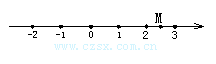
9．已知6x-2与4x-8互为相反数，求x的值．
10．数轴上离开原点的距离小于2的整数点的个数为x，不大于2的整数点的个数为y，等于2的整数点的个数为z，求x+y+z的值．
11．m，n互为相反数，a、b互为倒数，x=-（-4），求
+2006（m+n）+x的值．
答案：
一、针对训练
1．D 提示：+1与-2是符号不同的两个数，但它们不是互为相反数，故A错误，0的相反数是0，故B错误；的相反数是-，而-3.14是-的近似值，故C错误；0.5的相反数是-0.5，即-，故D正确．
2．B 提示：C、D在原点两旁，且到原点距离相等．
3．（1）-2 3.5
（2）-（a-b）
-（2x+y-z） （3）-
提示：（1）由-x=2，求x，即已知x的相反数是-2，求x，也就是求2的相反数；由x=-3.5，可得-x=-（-3.5）=3.5；
（2）求（2）中的相反数，只需在每个数前面加上一个“－”即可．
（3）由a+=0，求a，即求的相反数．
4．B 提示：a=-2
5．B 提示：互为相反数的两数之和为0；反之也成立．
6．B 提示：a+=0，
7．（1）-2 （2）7.2
（3）3 （4）-2
提示：利用相反数定义．
8．（1）； （2）2003；
（3）-4.25； （4）a+1．
二、递进演练：
1．B 2．A
3．（1） （2）2002
（3）- （4）b-a
4．C 导解：与3．14是两个不同的概念．
5．B A 导解：先化简符号，再分析．
6．D 导解：③④⑤正确．
7．解：如图-4<-3.5<-2.5<-2<2<2.5<3.5<4．
8．B 导解：M点表示的数为2.5．
9．解：依题意，得6x-2+4x-8=0，x=1．
10．解：到原点的距离小于2的整数点有-1，0，1三个；不大于2的整数点有-2，-1，0，1，2五个；等于2的整数点有-2，2两个，即x=3，y=5，z=2，故x+y+z=10．
11．解：由m、n互为相反数，得m+n=0；由a、b互为倒数，得ab=1；x=-（-4）=4，故+2006（m+n）+x=+2006×0+4=4．