七年级数学走进数学世界单元测试2

第一章 走进数学世界单元测试题

一、选择题:(每小题3分,共24分)

1.下图是飞行棋的一颗骰子,根据图中A、B、C三种状态的显示的数字,推出“?”处的数是(　 )

　　　　 　　　　　 

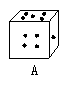
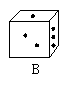
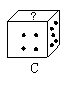
　 A.1点　  B.2点　　C.3点　　D.6点

2.用一根52厘米长的铁丝,恰好可以焊成一个长6厘米,宽4厘米,高____ 厘米的长方体框架.(　 )

　 A.2 　 B.3 　　C.4　　 D.5

3.把一个圆柱削成一个最大的圆锥,这个最大圆锥是削去部分的(　 )走进数

　 A.　　　　B.　　　　 C.2倍　　D.3倍

4.一台计算器原来售价100元,先降价15%,再提价15%,这时售价为(　 )

　 A.100元　　B.97.75元　　C.115元　 D.以上答案均不对

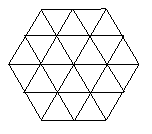
5.对24个面积为1的单位正三角形拼成如图所示的正六角形,我们把面积为4 的正三角形称为“希望形”,则图所示的不同的“希望形”共有(　 )

　 A.11个　 B.12个　 C.13个　 D.14个

6.图中的各种形状的硬纸,能适当折叠,围成正方体的是(　 )

　　　 

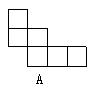
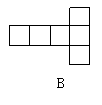
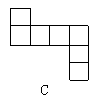
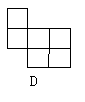
7.把一个平行四边形任意分割成两个梯形,这两个梯形的_______总是相等的(　 )

　 A.面积　  B.高　　C.上、下两底的和　　D.腰

8.某人在计算这四个分数的平均值时,误将其中一个分数看成了它的倒数, 他计算出的平均值与正确的结果最多相差(　 )

　 A. 　　 B. 　　C. 　　　 D.

二、填空题:(每小题3分,共24分)

9.小明语文、外语的平均分是81分,他的数学比语、数、外三门的平均分多5分,他的数学得_______.

10.某商品每件成本72元,原来按定价出售,每天可售出100件, 每件利润为成本的25%,后来按定价的90%出售,每天销售量提高到原来的2.5倍.照这样计算, 每天的利润比原来增加______元.

11.在4×4的方格图案中,共有_____个正方形;如果是6×6的方格图案, 有___个正方形;若是n×n的方格图案,那么有____个正方形.

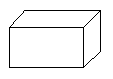
12.如图所示,用刀去切一个正方体,切口图形可能是__________.

13.17个连续整数的和是306,那么紧接在17个数后面的那17 个连续整数的和等于______.

14.10位评委为某体操运动员打分如下:

10、9.7、9.8、9.9、9.6、9.1、9.4、9.5、9.8、9.7

　去掉一个最高分和一个最低分,其余8个分数的平均数记为该运动员的得分, 则这个运动员的得分是_______.

15.某人以4km/h的速度从甲地步行到乙地,然后又以6km/h的速度从乙地返回甲地,那么某人往返一次的平均速度是________km/h.

16.如图所示的算式中不同的汉字表示不同的数字,那么,让+我+们+来+做+数+ 学+题=_________.

三、解答题:(共52分)

17.计算下列各题:(共24分)

　 (1) ;　　

(2) ;

　

 (3)200.2×20.01-200.1×19.99;

　

(4) .

18.从2开始,连续的偶数相加,它们的和的情况如表:(8分)

加数m的个数	和(S)
1	2=1×2
2	2+4=6=2×3
3	2+4+6=12=3×4
4	2+4+6+8=20=4×5
5	2+4+6+8+10=30=5×6

　　　当n个最小的连续偶数相加时,它们的和S与n之间有什么样的关系, 用公式表示出来,并由此计算:(1)2+4+6+…+202的值.(2)126+128+130+…300的值.

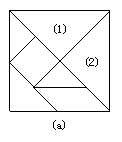
19.在图中,如图a用边长为8cm的正方形,做了一套七巧板,拼成如图b 所示的一座桥,求桥中阴影部分的面积.(8分)

　　　　　

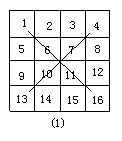
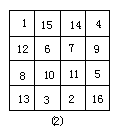
20.将1-16这16个自然数排成一个四阶幻方.(10分)

第1章 单元测试题答案:

一、1.D　2.B  3.A　4.B　5.B  6.B　7.B　8.A

二、

9.88.5;  10.11250;　11.30,91,1²+2²+3²+…+n²

12.三角形、四边形、五边形、六边形

三、

17.(1)1110　 (2) 　 (3)6.003　(4)

18.公式为 S=n(n+1)　(1)10302　(2)18744

19.32平方厘米

20.提示:首先将1~16各自然数依次填入图1,这时两条对角线上的数字之和都是34,我们对行、列进行调整,使得每行、列的和都变成34, 调整的对角线上的数应保持不动.

　　将2、3分别与15、14交换,5、8分别与12、9交换,得到图,它就是一个四阶幻方.