走进数学世界（第2讲）
【引言】
中学生朋友们，祝贺你们跨进了中学校园，数学世界欢迎你。
中学数学教学将结合具体的数学内容，从学生的生活实际出发，创设有助于学生自主学习的问题情境，引导学生通过实践、思考、探索、交流去获取知识，建立数学模型，形成解题技能，发展数学思维，掌握必要的基础知识，发展应用数学知识的意识与能力。我们将在轻松、愉快的气氛中与数学交朋友，学会去分析生活中的有趣的数学问题，了解宇宙之大，粒子之微，惊叹火箭之速，化工之巧，探索生物之谜，地球之变，让我们走进数学世界去了解数学的奥秘。诚然我们从小学已经开始学习数学这门学科，知道了整数和分数，学会了加、减、乘、除；认识了三角形、长方形、正方形、圆以及长方体、正方体、圆柱体和球体等图形，数学无处不在，数学伴我们成长。下面我们准备了十个例题，考查一下你的思维，是不是很聪明？
【典型例题分析】
例1． 李白买酒歌
李白街上走，提壶去买酒，
遇店加一倍，见花喝一斗，
三遇店和花，喝光壶中酒，
试问壶中原有多少酒？
算术头脑分析：（倒推法）喝光壶中酒
第三次见花前应有酒1斗第三次遇店前应有酒
斗第二次见花前应有酒（+1）斗第二次遇店前应有酒（+1）斗第一次见花前应有酒[（+1）+1]斗第一次遇店前应有酒 [（+1）+1]斗，此即壶里原有的酒。
解1： [（+1）+1]=
(斗) 答：略
说明：算术方法注重的是结论，运用例推的思维方法就可以解决李白买酒的数学问题，其实我们也有一些聪明的孩子已经掌握了代数的方法。
代数头脑分析 代数方法是用字母来代替数，顺着读题的顺序把每次买酒的数量用一个含字母的式子来表示，下面我们具体用分析如下：设壶中原有酒x斗第一次遇店后，壶中酒变为2x斗第一次见花后，壶中酒变为（2x-1）斗第二次遇店后，壶中酒为2（2x-1）斗第二次见花后，壶中酒变为2（2x-1）-1=（4x-3）斗第三次遇店后为2（4x-3）斗第三次见花后为2（4x-3）-1=0
解2：8x-7=0，得
斗 答：（略）
例2．我国四大发明之一的黑火药，它所用的原料是硫磺，硝酸钾和木炭，其比例是2∶15∶3，要配制这种火药
分析：在这个问题中，黑火药是一个整体，它包含三种物质硫磺、硝酸钾和木炭。
用算术头脑分析：三种原料混合在一起共重
硫磺占
，即
（克）
硝酸钾占
，即
（克）
木炭占
，即
（克）
答：三种原料各取
用代数头脑分析：在比例问题中，通常设每一份为x
根据题意得：2x+15x+3x=640，解得x=32
所以2x=64（克） 15x=480（克） 3x=96（克）
答：（略）
例3．时钟大家都很熟悉，请你观察并计算一下，在两点和三点之间，时钟上的分针和时针重合的时刻。
分析：针面是圆的，可以用两种计时单位来计算。
解法一：把钟面的圆盘边缘分成60格，分针每分钟走1格，时针每分钟走
格；设在两点x分时，时针和分针重合。这时分针走了x格，时针走了x格，重合时时针比分针少走了10格（时针是从第10个格出发走的）。由题意得x-x=10，解得x=
，
答：在两点
分时，时针与分针重合。
解法二：由于时针、分针是绕圆心旋转，分针60分钟可旋转一圈360°，那么分针每分钟转6°，时针每分钟转度，设在两点x分时，时针和分针重合。这时分针转了6x度，时针转了x度，重合时时针比分针少转了60度（时针是从钟面上2处开始旋转的）由题意得
，解得
，答：（略）。
同学们，你们可以仿造上面的例题编一个在三点和四点之间，分针和时针成一条直线的应用题，再试着求一求，你感到难不难？
例4．莱蒙托夫是俄国著名的诗人，爱好数学。有一次，他给一些军官表演猜数游戏。他请一名军官随便想好一个数，不要说出来，然后请这个军官将想好的这个数加上25，再加上125，减去37，再减去最初想好的这个数，把得到的数乘以5，最后再除以2，这时，莱蒙托夫说，我可以猜出你算出的结果，他问那个军官：“此数是282.5对吗？”那个军官非常吃惊，因为莱蒙托夫并不知道他想的是什么数，却得到了和他完全一样的结果。奥秘在哪里呢？请你用字母表示这个数，就能解开这个谜。
解：设那个军官想好的数为a
由题意得：（a+25+125-37-a）×5÷2=282.5
例5．托尔斯泰的割草问题
割草队要收割两块草地，其中一块比另一块大1倍，全队在大的一块草地上割了一上午，到了下午就分成两半，一半人继续留在大块草地上，到晚上正好把大块草地的草割完。另一半人转移到小块草地上，到了晚上还未割完，还剩下一小块。第二天，这剩下的一小块由一个割草队员花了一整天刚好割完。问这个割草队共有几人？
算术头脑分析：在大块草地上割草队全体割了半天，全队的一半人又割了半天，这就是，这一半人要花3个半天收割完这大块草地。也就是说，全队一半的人在半天时间内收割了大块草地的
。由于大块草地比小块草地大一倍，所以在小块草地上，半队人割半天后剩下的草地为大块草地的
。由于这剩下的一小块地正好由一个割草队员割完，即一个割草队员一天可割大块草地的
。而全队人在一天中共割了大块草地的
，所以割草队的总人数为
。
我们如果利用图解法也很方便，如右图：
 |
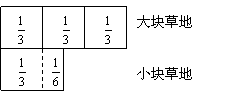代数头脑分析：
设割草队人数为x，每人每天割草面积为a，由题意可知：
大块草地面积为：
小块草地面积为：
由于大块草地比小块草地大一倍，故有：
两边都除以
（>0），解得x=8 答：割草队共有8人。
例6．立达中学第5中队的少先队员们去运河公园植树。已知树苗的成活率在75%—80%之间，为了确保1200棵树成活，第5中队的少年队员们，最少要栽种多少棵树苗？
分析：树苗的成活率在75%到80%之间，那么也就是说如果成活率低需要的树苗就多，需1600棵；如果成活率高，需要的树苗就少，需1500棵。因此为了确保1200棵树成活，就要细心呵护小树苗，让成活率达到最高时，栽种的最少树苗为1500棵。
例7．一幢八层楼房，由第一层到第二层有21级台阶，以后每上一层少2级台阶，求小强由第三层到达第八层共走了多少级台阶？
分析：上楼走楼梯与种树的道理一样
由一层到八层共有7个楼梯，它们是：
21+19+17+15+13+11+9
由第三层到达第八层共走了
17+15+13+11+9=65（级）
注意：由于缺乏生活经验，可能会出现走8个楼梯的错误。
例8．果子成熟后，从树上落到地面。它落下的高度与经过的时间有下面的关系：
| 时间t(秒) | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1 | …… |
| 高度h(米) | 5×0.25 | 5×0.36 | 5×0.49 | 5×0.64 | 5×0.81 | 5×1 | …… |
请你猜测一下用t表示h的公式。并用公式计算一下果子经过0.55秒落到地上，这个果子离地面的高度是多少米？（精确到0.01）
分析：通过列表给出的数据，我们发现了规律：5×0.25=5×0. 52
5×0.36= 5×0. 62 …… ∴公式h=5t2
当t=0.55秒时，高度h=5×0. 552=1.5125≈1.51（米）
请同学们自己来完成解题过程，要注意表述完整、清晰。
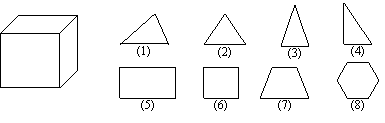例9．将正方体用刀切去一块，可得到下列哪些图形？不能得到的图形是哪一个？
分析：这是一道空间想象能力的题目，要通过观察，实践、摸索、总结，才能够全面地给出答案。我们不注重你的结论，而更看重的是你思考的过程，实践出真知，让我们动手，动脑，试一试吧！
例10．阅读科学家的故事。
哥德巴赫猜想与陈景润
早在
我们可以验证这个结论，例如：
6=3+3；
8=3+5；
10=3+7=5+5；
12=5+7；
14=3+11；
16=3+13=5+11；
18=5+13=7+11；
20=3+17=7+13；
22=3+19=5+17=11+11；
24=5+19=7+17=11+13；
26=3+23=5+21=7+19=13+13；
……
同学们也可自己试一试，任意取一个偶数（例如1000，1998），将它写成两个素数之和。
有人对一个一个偶数都进行了验算，一直算到3亿多，都表明这个猜想是对的，但是这还不能说明哥德巴赫猜想对于全部大偶数都是正确的，它的正确性还有待于研究。
欧拉和哥德巴赫一生都没能证明这个论断，以后的200年里，也没有哪位数学家给出证明。因此，直到今日，这只能称为一个猜想，这个猜想也就是著名的哥德巴赫猜想。这是一个世界上有名的难题，被誉为数学王冠上的一颗明珠。1900年，德国数学家希尔伯特在巴黎召开的第二届国际数学家大会上，提出了23个他认为最重要的没有解决的数学问题，这23个问题预示着20世纪数学研究的方向，许多数学家分别在解决这些问题方面作了巨大的努力，取得了丰硕的成果，哥德巴赫猜想问题就是希尔伯特第8问题（素数问题）的一部分。
我国著名数学家陈景润潜心研究了一系列著名的数论问题，特别是在哥德巴赫猜想问题的研究上，得到了目前世界上最好的结果，1966年5月，他证明了：每一个充分大的偶数都可以表示为一个素数和一个不超过2个素因子的积的和。
这个结果就是国际上公认的以陈景润的名字命名的陈氏定理。陈景润写出的（1，2）的证明长达200页，他的证明引起国际数学界的关注，称他的论文是解析数论的名作，是筛法的光辉顶点，是对研究哥德巴赫猜想的重大贡献。
至今为止，对哥德巴赫猜想的研究还没有结束，还有从（1，2）到（1，1）这最艰难的一步。英国数学家哈代（1877—1947）1921年在哥本哈根数学会上说：“哥德巴赫猜想可能是没有解决的数学问题中最困难的一个”。现在这颗皇冠上的明珠正在峰顶上闪耀，但她只属于那些勤奋踏实、不畏艰险、勇于攀登的攀登者。
【同步练习】
1．小华买了60分和80分的邮票共10枚，花了7元2角，那么60分和80分的邮票各买了几枚？
2．银行计算利息是存入的钱数（本金）与存入的时间数（期数）及每期的利率的积。某人将1万元按一年定期储蓄存入银行，月利率是1.88‰（读作千分之一点八八），到期后交利息税20%，问此人最后可得利息为多少元？
3．运用加、减、乘、除四种运算，如何由四个数2，7，10，4（每个数只能用一次）得到24，你能想出几个算式？写出来。
4．今年5月1日是星期三，你能否推算出今年10月1日是星期几？
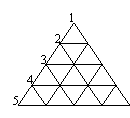
5．如图，线与线的交点个数由1+2+3+4+5得15个，
（1）图中的三角形个数为多少个？
（2）是点多呢？还是三角形多？
（3）你能写出数三角形个数的方法吗？如果再增加一排，会有多少个三角形呢？
6．电影院的座位数如下表所示：
（1）如果电影院有20排座位，那么电影院共有多少座位。
（2）
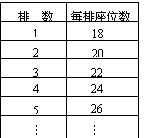记
为第n排的座位数，试用n的代数式表示。
7．某中队48人去游乐场游览，游乐场售票处规定：门票一人券每张10元，十人券每张70元，他们动脑筋想出了一种购买门票花费最少的办法，请你想一想最少要花多少元？
8．“从
9．某服装店同时卖出两套服装，每套均卖168元，以成本计算，其中一套盈利20%，另一套亏本20%，问这次出售服装，是赚钱还是赔钱？
10．妈妈让小明给客人烧水沏茶。他计算了一下时间，洗水壶需用1分，烧开水需用15分，洗茶壶需用1分，洗茶杯需用1分，拿茶叶需用2分。小明估算了一下，完成这些工作需花20分。为了使客人早喝上茶，按你认为最合理的安排，多少分就能沏茶了？
【练习答案】
1．买60分邮票4枚，80分邮票6枚
2．180.48元
3．（10-2）×（7-4）； 2×4×（10-7）； 7×（4÷2）+10；等
4．今年10月1日是星期二
5．（1）共计27个
（2）此图中三角形的个数多
（3）数三角形的个数要掌握规律，从小到大来数
有一个小三角形的有1+3+5+7=16个
由4个小三角形组成的有1+2+3+1=7个
由9个小三角形组成的有1+2=3个
由16个小三角形组成的有1个
如果再增加一排，会有48个
6．（1）740 （2）
7．买五张十人券共花费350元，如果把多余的两张再带两个人进游乐场，收每人7元的话，只要花费336元。
8． 135元
9． 原价分别为140元和210元，共计350元，现两套卖得168×2=336（元）因此赔了。
10．16分钟。这样安排，
洗水壶（1分）烧开水（15分）
利用烧开水同时：洗茶壶（1分）洗茶杯（1分）拿茶叶（2分）