2.6 有理数的加法
一、课内训练
1．计算：
（1）（+2）+（+5）； （2）（-2）+（-3）； （3）（-2）+（+5）；
（4）（+2）+（-5）； （5）（+6
）+（-5
）
2．计算：（1）（-8）+（-2）+2+（-）+12；
（2）[（+
）+（-3.5）+（-6）]+[（+2.5）+（+6）+（+
）]．
3．在1，-1，-2这三个数中，任意两数之和最大的是（ ）．
A．1 B．
4．如果两个有理数的和为负数，那么这两个有理数（ ）
A．都是正数 B．至少有一个正数
C．都是负数 D．至少有一个负数
5．（+3.375）+[（-1.92）+（-1.375）+（-5.01）+（-0.08）]．
6．计算[（+）+（-3.5）+（-6）]+[（+2.5）+（+6）+（+）]
7．一辆汽车沿着一条南北向的公路来回行驶，某一天早晨从A地出发，晚上最后达到B地，约定向北为正方向（如+7表示汽车向北行驶
+18.3，-9.5，+7.1，-14，-6.2，+13，-6.8，-8.5．
请你根据计算回答：
（1）B地在A地何方，相距多少千米？
（2）若汽车行驶每千米耗油
二、课外演练
1．计算：（1）（-2）+（-8）=________；（2）（-8）+（+6）=_____；
（3）（-7）+0=_______； （4）（-18）+（+18）=_______；
（5）8+（-2）=_______； （6）-
+=________．
2．水位上升7厘米，又下降3厘米，那么现在的水位比原水位________．
3．下列计算中，错误的是（ ）
A．（+
）+（-
）=-
B．（-）+（-）=-
C．（-）+（+）=-
D．（+）+（-）=0
4．下列计算结果是负数的是（ ）
A．0+[-（-3）] B．-1+
C．-1
+2.75
D．│-+（-
）│
5．下列说法中，正确的是（ ）
A．两个有理数的和总比其中的一个加数大;
B．两个有理数的绝对值的和与它们和的绝对值相等;
C．任何有理数与它的相反数的和是零;
D．任何有理数与它的绝对值的和是零
6．3
+（-2.53）+（-2
）+（+3.53）+（-）
=[3+（-）]+[（-2.53）+（+3.53）]+（-2），这个运算应用了（ ）
A．加法的交换律 B．加法的结合律
C．加法的交换律和结合律 D．以上均不对
7．如果三个有理数a+b+c=0，则（ ）
A．三个数不可能同号 B．三个数一定都是0
C．一定有两个数互为相反数 D．一定有一个数等于其余两个数的和
8．计算下列各题：
（1）（-51）+（+12）+（-7）+（-11）+（+36）+（+17）；
（2）37.5+（+28
）+[（-46）+（-25
）]．
9．用两种方法解：
（1）（-41）+18+（-39）+12； （2）+（-
）+
+（-
）++（-）．
10．若│a│=3，│b│=1，则代数式a+b的值为（ ）
A．4 B．
11．10筐苹果，以每筐25千克为准，超过的千克数记作正数，不足的千克数记作负数，称重的记录如下：+3，-4，+1.5，+5，-1.5，-3，-3，+3.5，-2，+4.5，求这10筐苹果的总重量．
12．分别在如图所示的空格内填上适当的数，使得每行每列的三个数之和为零．
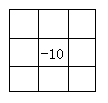
13．计算：
（1）（1-）+（-）+（-）+…+（
-
）；
（2）
+
+
+…+
．
答案：
一、课内训练
1．（1）（+2）+（+5）=+（│+2│+│+5│）=+（2+5）=7．
（2）（-2）+（-3）=-（│-2│+│-3│）=-（2+3）=-5．
（3）（-2）+（+5）=+（│+5│-│-2│）=+（5-2）=3．
（4）（+2）+（-5）=-（│-5│-│+2│）=-（5-2）=-3．
（5）（+6）+（-5）=[（+6）+（+）]+[（-5）+（-）]
=[（+6）+（-5）]+[（+）+（-）]=1+（-）=．
提示：有理数加法运算，确定符号是关键，首先要判定两个数的大小，其次利用有理数加法法则进行计算：（1）～（4）按有理数加的运算法则进行即可；（5）中加数为带分数，若直接根据加法法则，先确定符号，后把两数的绝对值化为假分数，再通分计算出结果，则计算较为复杂．我们可将两数的整数部分和分数部分分开相加，然后再把结果相加．
2．（1）原式=（2+12）+[（-8）+（-2）+（-）]
=14+（-11）=3；
（2）原式=（+）+（-3.5）+（-6）+（+2.5）+（+6）+（+）
=[（+）+（+）]+[（+2.5）+（-3.5）]+[（-6）+（+6）]
=
+（-1）+0=0．
提示：对于多个有理数相加的问题，常常运用加法的交换律和结合律，把同号的数相结合，把互为相反数的数相结合，把同号数中间分母的分数相结合，以达到计算简便、迅速的目的．
3．1+（-1）=0；1+（-2）=-（│-2│-│1│）=-（2-1）=-1；
-1-2=-1+（-2）=-（│-1│+│-2│）=-（1+2）=-3．
又因为：0>-1>-3，所以选B．
提示：从这三个数中，任取两个数共有1，-1；1，-2；-1，-2三种情况，分别算出这种情况下两数的和，再选择和最大的．
4．D
5．-5.01 提示：将（+3.375）与（-1.375）相加，（-1.92）与（-0.08）相加．
6．0 提示：利用运算律解．
7．解：（1）B地在A地南6.6千米
（2）耗油为
提示：在求用多少油时，应考虑所有路程．
二、课外演练
1．（1）-10 （2）-2 （3）-7 （4）0 （5）6 （6）-1
2．上升4厘米 导解：设原水位为0厘米，则现在水位为0+7-3=4厘米．
3．C 4．B
5．C 导解：-2+（-1）=-3和-3比-2，-1都小，A错；
│-2│+│+3│=5，
而│（-2）+（+3）│=1，有│-2│+│+3│≠│（-2）+（+3）│，B错；
2+│2│≠0，D错，只有C对．
6．C 7．A 导解：因为（a+b）+c=0，故a+b与c互为相反数．
8．（1）-4 （2）-5 导解：注意应用加法交换律和结合律．
9．解：（1）方法一：原式=[（-41）+（-39）]+（18+12）=-80+30=-50．
方法二：原式=[（-41）+18]+[（-39）+12]=-23+（-27）=-50．
（2）方法一：原式= [+（-）]+[（-）+]+[+（-）
=
+（-1）+（+1）=．
方法二：原式=（++）+[（-）+（-）+（-）]
=
=
=
10．D 导解：a=±3，b=±1．
11．解：超过或不足的总数为：
（+3）+（-4）+（+1.5）+（+5）+（-1.5）+（-3）+（-3）+3.5+（-2）+（+4.5）
=4（千克），25×10+4=250+4=254（千克）．
12．解：如图 导解：先填各行各列中间空格，再填其他空格．
13．解：（1）去括号得到：1-+-+-+…+-
=1-=
．
（2）因为=1-，=-，=-，
所以原式=（1-）+（-）+（-）+…+（-）
=1-=．