有理数及其运算（2.1—2.7）测试
班级___________________ 姓名__________ 得分____ _______
一、填空题:（每空2分，共40分）
1. 如果向东运动
2. 所有的有理数都能用数轴上的 来表示.
3. 数轴上原点右边的点表示 ，数轴上原点左边的点表示 ，原点表示 .
4. 数轴上表示—3的点到原点的距离是 个单位，那么到原点的距离等于3个单位的点表示的数是 .
5. 引入负数后，同学们学的数已扩充为有理数了。我们可以把有理数分为_______和________.
6. 如果a﹥0，那么在数轴上a对应的点在原点 ，-a对应的点在原点 .-a可以在原点的右边吗？答： .
7. 
的相反数是
，绝对值是
.
8. 绝对值在2与5之间的整数有 .
9. 小明写作业时不慎将墨水滴在数轴上，根据图中的数值，判定墨迹盖住部分的整数共有 个．
–6 -5 –4 –3 –2 -1 0 1 2 3 5 6
10. 如果a，b互为相反数，那么a+b= .
11. 比较下列各数的大小：（填“>”、“<”或“=”）
____ 0, 
_____
, 
_______
, 
0。
二.选择题（每题2分，共20分.）
12. 下面关于有理数的说法正确的是【 】
A. 有理数可分为正有理数和负有理数两大类.
B. 正整数集合与负整数集合合在一起就构成整数集合
C. 正数和负数统称为有理数 D. 正数、负数和零统称为有理数
13. 有理数中相反数等于本身的数是【 】
A. 1
B.
14. 有理数中绝对值最小的数是【 】
A. -1
B.
15. 一个数的绝对值是它本身，则这个数必为【 】
A. 这个数必为正数；B. 这个数必为0；C. 这个数是正数和0；D. 这个数必为负数
16. 一种面粉的质量标识为“25±0.25千克”，则下列面粉中合格的有【 】
A．24.70千克 B．25.30千克 C．25.51千克 D．24.80千克
17. 若两个数的和是负数，那么一定是【 】
A. 这两个数都是负数 B. 两个加数中，一个是负数，另一个是0
C. 一个加数是正数，另一个加数是负数，且负数的绝对值较大；D. 以上三种均有可能
18. 两个有理数的和为零，则这两个有理数一定【 】
A. 都是零 B. 至少有一个是零 C. 一正一负 D. 互为相反数
19. 一个数大于另一个数的绝对值，则这两个数的和是【 】
A. 正数 B. 零 C. 负数 D. 和的符号无法确定
20. 一个正数的绝对值小于另一个负数的绝对值，则两数和【 】
A. 正数 B. 负数 C. 零 D. 不能确定和的符号
21. 比3的相反数小3的数是【 】
A. －6 B.
三、解答题：（共40分）
22. 你想提高计算的准确率吗？不妨试试“一步一回头”.抄题与计算时每写一个数都要回头看一下是否有误.开始时可能感觉很慢，一旦形成习惯就会快起来的！计算下列各题：(1—8题，每题1分，9—12题，每题2分，共16分)
（1）（―3）＋（－7）； （2）（＋12）＋（－29）； （3）
；
（4）（－3.6）＋（－2.5）； （5）（＋2）－（＋9）； （6）（－3.8）－（＋4.7）；
（7） 
； （8） 
；
(9)（―4）＋（＋5）＋（―10）＋（＋4）；
（10） 
；
（11）
；
(12) （＋4.7）―（―8.9）－（＋7.5）＋（―6）。
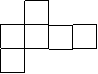23. （3分）下图是一个正方体的展开图，请在六个正方形中各添入一个数，使得按虚线折叠成正方体后，相对面上的两数互为相反数.
24.（4分）10袋小麦, 如果以40千克为准，超过的千克数记作正数，不足的千克数记做负数.称重的纪录如下：
＋2，＋1，―0.5，―1，―2，＋3，―0.5，―1，―1，0
这10袋小麦的总重量是多少千克？
25. （4分）下表列出了国外几大个城市与北京的时差（带正号的数表示同一时刻比北京时间早的小时数）
| 城市 | 纽约 | 巴黎 | 东京 |
| 与北京的时差 | －13 | －7 | +1 |
（1） 如果现在是北京时间上午8：00，那么东京时间是多少？
（2） 如果小强在北京时间下午15：00打电话给远在纽约的姑姑，你认为合适吗？
26. （4分）下表是某中学七年级5名学生的体重情况，试完成下表
| 姓名 | 小颖 | 小明 | 小刚 | 小京 | 小宁 |
| 体重（千克） | 34 | 45 | |||
| 体重与平均体重的差 | －7 | ＋3 | －4 | 0 |
（1） 谁最重？谁最轻？
（2） 最重的与最轻的相差多少？
27. （6分） 某摩托车厂本周内计划每日生产300辆摩托车，由于工人实行轮休，每日上班人数不一定相等，实际每日生产量与计划量相比情况如下表（增加的车辆数为正数，减少的车辆数为负数）
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | －5 | +7 | －3 | +4 | +10 | －9 | －25 |
（1） 本周三生产了多少辆摩托车？
（2） 本周总生产量与计划生产量相比，是增加还是减少？
（3） 产量最多的一天比产量最少的一天多生产了多少辆？
28. （3分） 观察下面一列数，探究其中的规律：
—1，
，
，
，
，
（1） 填空：第11，12，13三个数分别是 ， ， ；
（2） 第2008个数是什么？
（3） 如果这列数无限排列下去，与哪个数越来越接近？