2.7有理数的减法
一、课内训练
1． 计算：
（1）（-6）-（-3）；（2）（-2）-（+1）；（3）0-（-2.5）-（+1.5）-（-3）。
2． 计算:0-（-1.52）-（+7.52）-（-13）。
3． 下面是某同学计算-
解：原式=-10+（-8）+7+5=-18+7+5=-6。
请你判断他是做对了还是做错了，如果做对了，请你写出每一步的计算依据；如果做错了，请你改正过来。
4．（1）和是-2.7，一个加数是0.1，求另一个加数；
（2）两数之差为0.57，被减数是-0.35，求减数。
5． 较-
与-
的大小。
6． 在数轴上，设A点表示-3，AB的距离是4，则B点表示______.
7．A、B、C、D在数轴上的对应点分别为：-1、
、+
、+3.
（1）求A、B之间的距离；（2）求BC之间的距离；（3）求BD之间的距离；
（4）根据上述计算结果，探索两个点之间的距离与这两个点所对应的数之间的差的绝对值有什么关系？
二、课外演练
1.计算-2-1的结果是（ ）
A．-3 B．
2．下列各式运算正确的是（ ）
A．-1-1=0 B．-1-1=2
C．
-
=-
D．（-5）-（-2）+（-3）=-
3．-
比少（ ）
A．
B．- C． D．-
4．计算下列各题：
（1）（-53）+（+21）-（-79）-（+37）； （2）（+1）--1
+；
（3）0-（+）-（-）-（+
）-（-）；
（4）（-38）-（-21）-{（-50）-[（-70）-（-38）-（-28）]}．
5．a=29，b=-36，c=-216，则-a-b-c=_______．
6．重庆市某天的最高气温是
7．下列说法中正确的个数有（ ）
①两个有理数绝对值的和等于这两个数和的绝对值．②两个有理数和的绝对值为正数．③两个有理数差的绝对值等于这两个数绝对值的差．④两个有理数绝对值的差必为负数．
A．0个 B．1个 C．2个 D．3个
8．右一个有理数与它的相反数的差为一负数，则下列说法正确的是（ ）
A．这个有理数一定是负数 B．这个有理数一定是正数
C．这个有理数可能是正数也可能是负数
D．这个有理数只能为0
9．有一位同学连续记录了一周内每天气温的变化最高与最低的情况，如下表（单位：℃）
| 日期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 最高气温 | -3 | -6 | -2 | 3 | 5 | 8 | 11 |
| 最低气温 | -9 | -12 | -13 | -6 | -4 | -3 | -1 |
探究一：由表中数据分析：（1）本周内气温最高是______，最低是_______．
（2）一天中，温度差最大是星期______，温差是________．
（3）本周内的温差是_______．
探究二：由这一周的气温变化，估计天气变化的趋势是_______．
10．比0小5的数是_______，比3小10的数是_______，比a小-3的数是_______．
11．已知│a│=3，│b│=4，则│a-b│的值是（ ）
A．-1 B．
12．北京等5个城市的国际标准时间（单位：小时）可在数轴上表示如下：
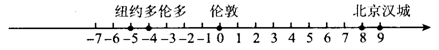
如果将两地国际标准时间的差称为时差，那么（ ）
A．汉城与纽约的时差为13小时;B．汉城与多伦多的时差为13小时
C．北京与纽约的时差为14小时;D．北京与多伦多的时差为14小时
13．数轴上A、B两点表示的有理数分别是-7与3
，试求A、B两点间的距离．
14．2004加上它的得到一个数，再减去所得数的，再加上所得数差的
，再减去所得数和的，……依此类推，一直到减去上一次所得和的
，求最后的差是多少？
答案：
一、课内训练
1．（1）（-6）-（-3）=（-6）+（+3）=-3；
（2）（-2）-（+1）=（-2）+（-1）=-3；
（3）0-（-2．5）-（+1．5）-（-3）=0+2．5+（-1．5）+3=4．
提示：计算有理数减法的关键是把减法转化为加法，在变换时，要注意变号．
2．7
3．这个同学的解答是错误的，正确的解法如下：
-
提示：在减法运算中既要改变运算符号，也要改变减数的性质符号，题中“-8-
4．（1）-2.8 提示：求-2.7-0.1．
（2）-0.92 提示：求-0.57+（-0.35）．
5．->- 提示：--（-）=
>0．
6．-7或1 提示：│xB-（-3）│=4．
7．（1）；（2）2；（3）3；
（4）两个点之间的距离等于这两个点对应的差的绝对值．
二、课外演练
1．A 2．C
3．A 导解：-（-）=。
4．解：（1）原式=（-53）+（+21）+（+79）+（-37）
=[-53+（-27）]+[（+21）+（+79）]
=（-90）+100=10．
（2）原式=（+1）+（-）+（-1）+
=[（1+）+]+[（-）+（-1）]
=（+2）+（-2）=．
（3）原式=0+（-）+（）+（-）+（+）
=[（-）+（-）]+ +=-++=．
4．原式=（-38）+（+21）-{（-50）-[（-70）+（+38）+（+28）]}
=（-17）-[（-50）-（-4）]=（-17）-[（-50）+（+4）]
=（-17）-（-46）=（-17）+（+46）=29．
5．223 导解：原式=-29-（-36）-（-216）．
6．12 导解：17-5=12（℃）．
7．A 导解：分同号、异号和0几种情况讨论．
8．A 导解：设这个数为a，则有a-（-a）<0．
9．解：（1）
10．-5
11．D 导解：a=±3，b=±4．
12．B
13．解：AB=│（-7）-（3）│=│（-7）+（-3）│=│-11│=11．
14．解：最后结果为
2004×（1+）（1-）（1+）（1-）…（1-）
=2004×（××
×
××
×…×
×
）
=2004．