2.6
有理数的加法
学习目标
1. 探索有理数的加法法则:
,
,
,
。
2．理解有理数加法的意义，并能准确地进行有理数的加法运算.
预习内容：认真阅读课本第35页到37页，根据课本“试验”完成尝试题一：
1．
根据要求列式计算：若规定收入为正，支出为负，求最终盈余或透支情况：
（1）
收入51元，支出27元。
（2）
支出51元，收入27元。
（3）
收入51元，收入27元。
（4）
支出51元，支出27元。
利用加法法则（请将学习目标中法则添加完整）根据课本例1完成尝试题二：
2．
计算：
（1） （+5）+（-21）
（2） （+12）+（+78）
（3） （-
）+（-
）
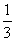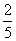（4） （+2.1）+(-1.2)
（5） （-0.5）+︱-3.5︱
（6） 5+（-5）
（7）0+（-3）
3．
若︱x︱=5，︱y︱=2，求x+y的植
4．
填空：
（1） +11=27 （2）7+ =4
（3）（-9）+ =9
（4）12+ =0
（5）（-8）+ =
-15 （6） +（-13）= -6
5．
土星表面的夜间平均温度为-150℃，白天比夜间高27℃，那么白天的平均温度是多少度？
| 课堂练习 1． 判断： （1）两个有理数相加，和一定大于每一个加数（ ） （2）一个正数与一个负数相加得正数（ ） （3）两个负数和的绝对值一定等于他们绝对值的和（ ） （4）两个正数相加和为正数（ ） （5）两个负数相加绝对值相减（ ） （6）正数加负数和一定等于零（ ） 2． 填空 （1） +（-13）=5 （2） +（+9）= -10 （3） +（-5）=+7 （4）（-9）+ = -3 （5）（-13）+ =25 （6）（+4）+ =0 3． 计算： （1）（-19）+（+12） （2）-（-32）+（-13） （3）（-7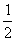 ）+（-5） （4）68+（-46） 4． 列式并计算： （1）-4.5的绝对值与5.5的相反数的和 （2）-7与-3的相反数的和的绝对值 （3）-1.5的相反数与1.2的倒数的和 （4）绝对值小于5.2的所有整数的和 5． 若︱x︱=3, ︱y︱=5， （1）求x+y； （2）若x<y，求x+y。 6． 若︱x+2︱与︱y-9︱互为相反数，求x+y的植。 7． 用“>”或“<”号填空 （1）若m>0，n>0, 则m+n 0；（2）若m<0, n<0，则m+n 0； （3）若m>0，n<0，且︱m︱>︱n︱，则m+n 0； （4）若m<0，n>0，且︱m︱>︱n︱，则m+n 0。 | |