第5章 数据的收集与表示 典型例题，强化训练及单元检测
课标要求
1.通过一些实例，体会数据的作用，养成用数据说话的习惯.
2.要求学生能设计统计表，能制作条形统计图、折线统计图，会画扇形统计图.
3.会借助频数或频率，体会随机事件发生的可能性是有大小的.
典型例题
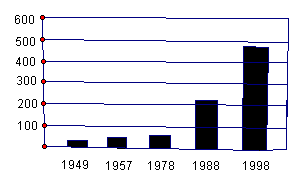例1 在《中国日报》1999年10月1日的国庆专刊上，刊登了有关中国城市建设在建国50年来的发展情况，下图摘录了一则中国城市数量统计图.你从这个统计图中获得了哪些信息？
解：从这个统计图中可以看出，在新中国成立后的近30年时间里，我国城市数量的发展相当缓慢，30年内才增加了一倍左右.从1978年我国实行改革开放政策，带来了城市的迅猛发展，到1998年城市数量差不多是建国初期的100倍.
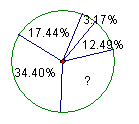例2 （2004年海口中考题）第五次全国人口普查资料
显示 ,我省2000年总人口为786.75万，
图中表示我省2000年接受初中教育这
一类别的数据丢失了，那么，结合图中信息，可
推知2000年我省接受初中教育的人
数为（ ）
A. 24.94 B. 255.96 C.270.64 D. 137.21
解：由图可知：
2000年我省接受初中教育的人数为：
(1- 34.40% - 17.44%-3.17%- 12.49% )×786.75 = 255.96(万元)
例3 （2002年辽宁省中考题）初中生的视力状况受到全社会的广泛关注，某市有关部门对全市3万名初中生视力状况进行了一次抽样调查，如图是利用所得数据绘制的频数分布直方图（长方形的高表示该组人数），根椐图中所提供的信息回答下列问题：
1．本次调查共抽查多少名学生？
2．在这个问题中的样本指什么？
 |
100---- 人数
90-------------------
60-----------------------------
40-----------
30---------------------------------------
20------
3.95 4.25 4.55 4.85 5.15 5.45 视力
3．如果视力在4.9～5.1（含4.9、5.1）均属正常，那么全市有多少初中生的视力正常？
4．如果你随机的遇到这些学生中的一位，那么这位学生最有可能属于哪种视力情况？
解：1.本次共抽测了 20+40+90+60+30=240（人）
2．样本是指所抽测的240名学生的视力.
3．人数约为30 000×60/240=7 500(人)
4．因为视力在4.55～4.85的学生最多，所以这位学生最有可能就是视力为：4.55～4.85.
说明：1、样本得出的结果，估计总体的结果，如样本中正常的比例为60/240=1/4,可视为总体中正常的比例.2、根椐这一比例和总体所含个体的人数，即可求得总体中正常人数的估计值.
强化练习
1.在一个正方体的6个面上分别标上数字，使得“2”朝上的可能性为_______________
| 8.0 | 8.3 | 9.1 | 8.5 | 8.2 | 8.4 | 9.0 |
2.南京长江大桥连续七天的车流量（每天过桥车辆次数）分别如下所示（单位：千辆/日），这七天平均车流量为_________千辆/日.
3.下列说法中，哪些是确定的？哪些是可能的？哪些是不可能的？哪些是不太可能的？
(1)地球绕着太阳转，月亮绕着地球转.（ ）
(2)一个初三年级的男生的平均身高与女生的平均身高一定相等.（ ）
(3)夏天某市体育课后，每位学生都去商店卖冷饮吃.（ ）
(4)一人去体彩摸奖，一摸就中了一等奖.（ ）
4.某校为了了解初一年级的学习状况，在这个年级抽取了50名学生，对数学学科进行测试，将所得成绩整理，分成五组，列表如下.试问：
(1)成绩在90分以上的频率是_______.
(2)成绩优秀的人数有_______人（80分以上为优秀），占总人数的__________
(3)及格的人数有_____人，及格率是_____.
| 分 组 | 频 率 |
| 49．5～59.5 | 0．04 |
| 59．5～ 69.5 | 0．04 |
| 69．5～79.5 | 0．16 |
| 79．5～89.5 | 0．34 |
| 89．5～99.5 |
|
单元检测A卷
一、填空题
1.掷两枚分别标有1，2，3，4的四面体骰子，写出这个实验中的一个可能事件_____________; 写出这个实验中的一个必然事件_______________.
2.已知全班共40位学生，他们有的步行，有的骑车，还有的乘车来上学，根据以下已知信息完成统计表：
| 上学方式 | 步 行 | 骑 车 | 乘 车 |
| “正”字法记录 | 正正正 | ||
| 频 数 | 9 | ||
| 频 率 | 40% |
3.请你举出一个利用数据得出结果的例子_______________________________.
二、选择题
1.下列事件必然发生的是 （ ）
A.一个普通正方体骰子掷三次和为19
B.一副洗好的扑克牌任抽一张为奇数.
C.今天下雨.
D. 一个不透明的袋子里装有4的红球，2的白球，从中任取3个球，其中至少有2球同色.
2. 样本：7，12，11，10，13，8，7，14，9，10，8，11，10，8，10，9，12，9，13 ，11.那么这组数据落在范围8.5 ～ 11.5内的频率应该是（ ）
A. 0.65 B. 0.6 C. 0.5 D. 0.4
3. 一次体育测试中，10名女生完成仰卧起坐的个数如下：48，52，47，46，50，50，51，50，45，49，则这次体育测试中仰卧起坐个数大于50个的频率为（ ）.
A．0.3， B.0.4 C .0.5 D. 0.6
三、解答题
1.在一个不透明的口袋中装着大小、外形等一模一样的5个红球、3个蓝球和2个白球，他们已经在口袋中搅匀了.请判断以下事情是可能发生，还是不可能发生，或是必然发生，并说明理由.
(1)从口袋中人取一个球，是一个白球.
(2)从口袋中一次任意取出5个球，全是蓝球.
(3)从口袋中一次任意取出5个球，只有篮球和白球，没有红球.
(4)从口袋中一次任意取出6个球，恰好红、蓝、白三种颜色的球都齐了.
(5)从口袋中一次任意取出9个球，恰好红、蓝、白三种颜色的球都齐了.
2.请看以下材料：（摘自《新华社》有关报道）
| 世界人均住房建筑面积 （单位：平方米） |
| 高等收入国家 45 中高收入国家 30 中等收入国家 20 中低收入国家 18 低等收入国家 8 |
中国人均住房建筑面积
（单位：平方米）
1979年 7.2平方米
2000年 20.4平方米
2005年 22平方米
请回答以下问题：
(1)制作出不同收入类型国家人均住房建筑面积的条形统计图.
(2)制作出我国不同年代人均住房建筑面积的折线统计图.
(3)根据以上数据，说明我国人均住房条件的现状及未来发展趋势.
单元检测B卷
一、填空题
1.扇形统计图是利用圆和___________来表示_________和部分的关系，圆代表的是总体，即100%，而非具体的_______,圆的大小与总数量也无关.
2.已知一个县有40人参加全国初中物理竞赛，把他们的成绩分为六组，第一组到第四组的频数分别是10，5，7，6，第五组的频率是0.20，则第六组的频率是___________
3.某学校在全校进行了一个调查，共有3402人参加.内容是：你认为一名高素质的教师最需要具备如下哪个条件；较强的教学能力（604人），合理的知识结构（235人），对学生的爱心（838人）,现代教育观念（1725人）.请回答以下问题：从这次调查中，认为一名教师最需要具备的条件是_________,所占比例约为________.
二、 选择题
1.假如你想知道自己的步长，那么你的调查问题是（ ）
A .我自己 B .我每跨一步平均长度为多少？ C .步长 D.我走几步的长度
2.甲袋中装着1只红球9只白球，乙袋中装着9只红球1只白球，两个口袋中的球都已搅匀.想从两个口袋中摸出一个红球，那么选哪一个口袋成功的机会较大？( )
A .甲袋 B.乙袋 C . 两个都一样 D.两个都不行
三、解答题
1.小华的书架上有一些书，其中的三分之一是学习参考书，六分之一是学习工具书，剩下的都是科普等其它书籍.根据这些信息，你能做出表示每一类书籍具体数目的条形统计图吗？能做出表示每一类书籍所占比例的扇形统计图吗？如果能的话，请作出相应的统计图，如果不能请说明理由.
2.某人出生时身高为48厘米，上（右）图描述的是他的身高变化情况，此折线统计图是根据此人在出生时以及以后每五年的身高数据用折线连接而成的，此折线图表明此人12岁时身高为150厘米,请问这个数据一定是符合实际的吗？
3.根据有关人士介绍，1995年，我国信函总量为79.6亿件，1996年下降至78.7亿件，而1997年只有70亿件，1998年仍在缓慢下降.根据1998年上半年的统计数字，在全国邮政业务总量中，信函从去年同期的14.03%下降到11.41%.目前我国人均信函量每 年只有5.5件.
①如图所示，下面关于这几年的信函总量的条形统计图合理吗？如不合理，请你做出更合理的条形统计图.
②根据你所作的条形统计图再设计一个折线统计图反映从1995到1998年这四年来我国信函总量变化的情况，如何分析这种变化？
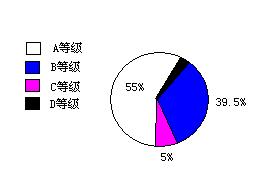
4. 我省课改实验区于2005年起实行初中毕业生综合素质评价，结果分为A、B、C、D四个等级.我省某区教育局为了了解评价情况，从全区3600名初中毕业生中任意抽取了200名学生的评价结果进行统计，得到如图所示扇形统计图：根据图中提供的信息，①请你求出样本中评定为D等级的学生占样本人数的百分之几？有多少人？②请你说明样本中众数落在哪一个等级？估计该区初三毕业生中众数所在等级的总人数大约是多少？
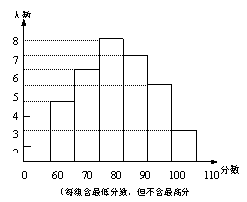
5
．某中学部分同学参加全国初中数学竞赛, 取得了优异的成绩，指导老师统计了所有参赛同学的成绩（成绩都是整数，试题满分120分），并且绘制了频率分布直方图.
请回答：
(1)该中学参加本次数学竞赛的有多少名同学？
(2)如果成绩在90分以上（含90分）的同学获奖，那么该中学参赛同学的获奖率是多少？
(3)图中还提供了其它信息，例如该中学没有获得满分的同学等等.请再写出两条信息.
6.生活中的数学(显示你解决生活中问题的能力喔!)
佳能电脑公司的李经理对2004年11月份电脑的销售情况做了调查，情况如下表：
| 每台价格(元) | 6000 | 4500 | 3800 | 3000 |
| 销量(台) | 20 | 40 | 60 | 30 |
请你回答下列问题：(1)2004年11月份电脑价格(与销售台数无关)组成的数据平均数为 ，中位数为 ，本月平均每天销售 台(11月份为30天)．
(2)价格为6000元一台的电脑，销售数量的频率是 ．
(3)如果你是该商场的经理，根据以上信息，应该如何组织货源.
7.市体校准备挑选一名跳高运动员参加全市中学生运动会，对跳高运动队的甲、乙两名运动员进行了8次选拔比赛.他们的成绩（单位：m）如下：
甲：1.70 1.65 1.68 1.69 1.72 1.73 1.68 1.67
乙：1.60 1.73 1.72 1.61 1.62 1.71 1.70 1.75
(1)甲、乙两名运动员的跳高平均成绩分别是多少？
(2)哪位运动员的成绩更为稳定？
(3)若预测，跳过1.65m就很可能获得冠军，该校为了获得冠军，可能选哪位运动员参赛？若预测跳过1.70m才能得冠军呢
第5单元参考答案
强化练习 1.1/6 2.8.5 3(1)确定 (2)不可能 (3) 不太可能(4) 可能 4.(1)0.42
(2)38,76% (3)48,96%
单元检测A卷：一、略 二、1.D 2.C 3.B 三、1.解：（1）可能发生。（2）可能发生。（3）可能发生。（4）可能发生。（5）必然发生
2.略。
单元检测B卷：一、1.扇形 、总体、数量 2. 0.1 3.现代教育观念，51%
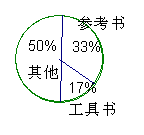二、1. B 2.B 三、 1.解：因为不知道书架上书的总数，又无法求出每一类书籍的具体数目，所以不能作出条形统计图；但是能作出扇形统计图。（如右图）
2.答：不一定符合实际，因为实际测量到的只有
此人在出生、5岁、10岁、15岁、20岁、25岁时
的身高这六个数据，其他年龄时的身高都是估计的，所以12岁时身高150cm也是一个估计值，可能是正确的，也可能是有误差的。
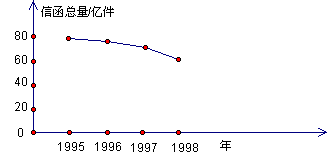3. 解：①不合理。正确图形应从0开始，而不是从50开始。（图略）。
②折线统计如下图所示，从折线统计图上可以看出我国信函总量在逐年下降，造成这一结果的原因是新兴通信手段以无可比拟的优越性向传统的信函发起挑战，电话、电子邮件、传真等现代通信手段已逐步成为人们生活中的一部分，也说明了社会在发展。
4.解：①样本中评为D等级的学生所占比例
为0.5%
评为D等级的学生人数为：0.5%×200=1
②众数落在A等级。
该区初三毕业生中众数所在等级人数约为：
3600×55%=1980
5. (1)4+6+8+7+5+2=32人(2)90分以上人数：7+5+2=14人
(3)该中学参赛同学的成绩均不低于60分。成绩在80—90分数的人数最多。
6. 25．(1)4325 4150 5 (2)0.13 (3)略(答案不唯一)