4.1 简单的立体图形 线段与角 典型例题及强化训练
课标要求
（1）点、线、面。通过丰富的实例，进一步认识点、线、面（如交通图上用点表示城市，屏幕上的画面是由点组成的）。 完成基本作图：作一条线段等于已知线段.
（2）角。①通过丰富的实例，进一步认识角。
②会比较角的大小，能估计一个角的大小，会计算角度的和与差，认识度、分、秒，会进行简单换算。
③了解角平分线。
④了解补角、余角，知道等角的余角相等、等角的补角相等。
（3）视图
①会画基本几何体（直棱柱、圆柱、圆锥、球）的三视图（主视图、左视图、俯视图），会判断简单物体的三视图，能根据三视图描述基本几何体或实物原型。
②了解直棱柱、圆锥的侧面展开图，能根据展开图判断和制作立体模型。
③了解基本几何体与其三视图、展开图（球除外）之间的关系；通过典型实例，知道这种关系在现实生活中的应用（如物体的包装）。
④观察与现实生活有关的图片（如照片、简单的模型图、平面图、地图等），了解并欣赏一些有趣的图形（如雪花曲线、莫比乌斯带）。
典型例题
例1.判断正误，并说明理由
①．两条直线如果有两个公共点，那么它们就有无数个公共点； （ ）
②．射线AP与射线PA的公共部分是线段PA； （ ）
③．有公共端点的两条射线叫做角； （ ）
④．互补的角就是平角； （ ）
⑤．经过三点中的每两个画直线，共可以画三条直线； （ ）
⑥．连结两点的线段，叫做这两点间的距离； （ ）
⑦．角的边的长短，决定了角的大小；
⑧．互余且相等的两个角都是45°的角； （ ）
⑨．若两个角互补，则其中一定有一个角是钝角； （ ）
⑩大于直角的角叫做钝角. （ ）
解：①．√．因为两点确定唯一的直线．
②．√，因为线段是射线的一部分．如图：
显然这句话是正确的．
③．× ， 因为角是有公共端点的两条射线组成的图形．
④．×．互补两角的和是180°，平角为180°．就量数来说，两者是相同的，但从“形”上说，互补两角不一定有公共顶点，故不一定组成平角．如下图
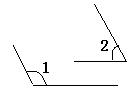
⑤．×．平面内三点可以在同一条直线上，也可以不在同一条直线上．
⑥． ×．连结两点的线段的长度，叫做这两点的距离．
⑦．×．角的大小，与组成角的两条射线张开的程度相关，或者说与射线绕着它的端点旋转过的平面部分的大小相关，与角的边画出部分的长短无关．
⑧．√，互余”即两角和为90°．
⑨．×． “互补”即两角和为180°．想一想：这里的两个角可能是怎样的两个角？
⑩×.钝角是大于直角而小于平角的角.
【注意】1.第⑤题中三个点的相互位置共有两种情况，如图
再如两角互补，这里的两角有两种情形，如图：
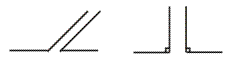
图（1） 图（2）
因此，互补的两个角中，可能有一个是钝角，也可能两个角都是直角，因此在作出判断前必须全面地考虑，这就要求有“分类讨论”的思想，“分类讨论”是数学中重要的思想方法之一．
2.注意数和形的区分与联系：“线段”表示的是“图形”，而“距离”指的是线段的“长度”，指的是一个“数量”，两者不能等同．
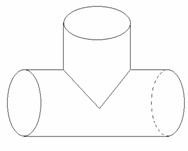
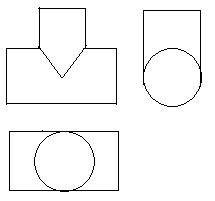
例2.如图：是一个水管的三叉接头，试画出它的三视图。
【注意】画三视图的原则是：长对齐，宽相等，高平齐。
例3.下面是正方体的展开图，每个平面内都标注了字母，请根据要求回答问题：
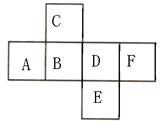
（1）和面A所对的会是哪一面？
（2）和B面所对的会是哪一面？
（3）面E会和哪些面平行？
答：（1）和面A所对的是面D；（2）和B面所对的是面F；（3）面E和面C平行。
例4.（1）线段DE上有A、B、C三个点，则图中共有多少条线段？
（2）若线段DE上有n个点呢？
解：（1）10条。
方法一：可先把点D作为一个端点，点A、B、C、E分别为另一个端点构成线段，再把点A作为一个端点，点B、C、E分别为另一个端点构成线段……依此类推，数出所有线段求和，即得结果．
方法二：5个点，每个点与另外一个点为端点可以组成一条线段，共有5×4条，但不计重复的应有
条，即10条。
（2）(n＋1)＋n＋(n－1)＋…＋3＋2＋1＝
（条）
例5．计算：（1）37°28′＋44°49′；（2）23．118°12′－37°37′×2；
（3）132°26′42″－41.325×3；（4）360°÷7（精确到分）．
解：（1）37°28′＋44°49′
＝81°77′
＝82°17′
（2）118°12′－37°37′×2
＝118°12′－75°14′
＝117°72′－75°14′
＝42°58′．
（3）法一 132°26′42″－41.325°×3
＝132.445－123.975
＝8.47．
法二 132°26′42″－41.325×3
＝132°26′42″－123.975
＝132°26′42″－12358′30″
＝131°86′42″－12358′30″
＝8°28′12″．
（4）360°÷7
＝51°＋3°÷7
＝51°＋25′＋5′÷7
＝51°＋25′＋300″÷7
≈51°＋25′＋43″
≈51°26′．
【注意】⑴1°＝60′，1′＝60″，低一级单位满“60”，要向高一级单位进“1”，由高一级单位借“1”要化成“60”加入低一级单位参与运算．
⑵在“度”、“分”、“秒”的混合运算中，可将“分”、“秒”化成度，也小数部分的度数可化成”“分”“秒”进行计算。
例6.已知∠α与∠β互为补角，且∠β的
比∠α大15°，求∠α的余角．
解：
由题意可得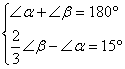
解之得
∴ ∠α的余角＝90°－∠α＝90°－63°＝27°．
答：∠α的余角是27°．
【注意】通过列方程或方程组解决几何问题是常用的方法，关键是选取适当的未知数。
强化训练
一．填空题
1．用一副三角板可以作出大于0°而小于180°的角的个数是 _________.
2．时钟的分针每60分钟转一圈，那么分针转900需________分钟，转1200需_______分钟，25分钟转________度.
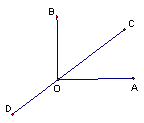
3．如图，四点A、B、C、D在一直线上，则图中有______条线段，有_______条射线；若AC=12cm，BD=8cm，且AD=3BC，则AB=________，BC=________，CD=________
4．已知有共公顶点的三条射线OA、OB、OC，若∠AOB=1200，
∠BOC=300，则∠AOC=_________
5．已知点A、B、C三个点在同一条直线上，若线段AB=8，BC=5，
则线段AC=_________
6．如图，已知OA⊥OB，直线CD经过顶点O，若
∠BOD：∠AOC=5：2，则∠AOC=_______∠BOD=__________
7．计算（1）23030′= 
,
;
（2）
;
.
8.要把木条固定在墙上至少要钉两颗钉子，这是因为___________________________。
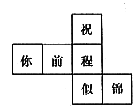
9.水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示.如右图,是一个正方体的平面展开图,若图中的“似”表示正方体的前面, “锦”表示右面, “程”表示下面.则“祝”、 “你”、 “前”分别表示正方体的______________________.
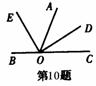10.如图，B、O、C在同一条直线上，OE平分
AOB，DO平分上AOC，则EOD＝_______．
二、选择题
1．下列各图中，分别画有直线AB，线段MN，射线DC，其中所给的两条线有交点的是( )
2．如果在一条直线上得到10条不同的线段，那么在这条直线上至少要选用（ ）个不同的点.
A、20 B、10 C、7 D、5
3．平面内两两相交的6条直线，其交点个数最少为m个，最多为n个，则m+n等于（ ）
A、12 B、16 C、20 D、以上都不对
4.在下列立体图形中，不属于多面体的是（ ）
A．正方体 B．三棱柱 C．长方体 D．圆锥体
5．（2004年河北省课程改革实验区）图中几何体的主视图是（ ）
三．解答题
1．(1) 一个角的余角比它的补角
还多1°，求这个角.
(2)已知互余两角的差为20°,求这两个角的度数.
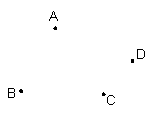
2．已知如图，设A、B、C、D、为4个居民小区，现要在四边形ABCD内建一个购物中心，试问应把购物中心建在何处，才能使4个居民小区到购物中心的距离之和最小？试在图中画出这个中心（用点P表示），不必说明理由
简单的立体图形 线和角
一、1.11； 2.15、20、150； 3.6、8、7cm、5cm、3cm ； 4.150°、90°；
5.13或3； 6. 60°、150°；7. ①23.5°、②
③
④
；
8. 两点确定一条直线的． 9.后面、上面、右面. 10. 90°
二．
| 题号 | 1 | 2 | 3 | 4 | 5 |
| 答案 | A | D | B | D | D |
三．1.解：⑴设这个角为x,则90－x=
解得 x=63
答：这个角为63.
⑵略
2.解：连结AC、BD交于点O.