§2．4 绝对值
基础巩固训练
一、选择题
1．下列各式中，等号不成立的是（ ）
A．│-4│=4 B．-│4│=-│-4│； C．│-4│=│4│ D．-│-4│=4
2．下列说法错误的是（ ）
A．一个正数的绝对值一定是正数； B．任何数的绝对值都是正数
C．一个负数的绝对值一定是正数； D．任何数的绝对值都不是负数
3．绝对值大于-3而不大于3的整数的个数有（ ）
A．3个 B．4个 C．5个 D．6个
4．若a，b是有理数，那么下列结论一定正确的是（ ）
A．若a<b，则│a│<│b│； B．若a>b，则│a│>│b│
C．若a=b，则│a│=│b│； D．若a≠b，则│a│≠│b│
5．若│a│=4，│b│=9，则│a+b│的值是（ ）
A．13 B．5 C．13或5 D．以上都不是
二、填空题
1．-2的绝对值是_______，
的绝对值是________，0的绝对值是_______．
2．│-
│=________，-│-1.5│=________，│-（-2）│=_______．
3．绝对值是+3．1的数是_________，绝对值小于2的整数是_________．
4．若│x│=5，则x=________，若│x-3│=0，则x=_________．
5．若│x│=│-7│，则x=_______，若│x-7│=2，则x=_________．
6．│3.14-
│=_______．
7．如图所示，数轴上有两个点A，B分别表示有理数a，b，根据图形填空．
a______b，│a│_______│b│，│a-b│=_________，│b-a│=________．
8．│-a│=-a成立的条件是________．
9．用“>”、“＝”或“<”填空:（1）-
_____
； （2）--
______│0．75│；
（3）-（3．6）______-│3．6│； （4）+-
________--．
三、解答题
1．如图所示，数轴上有四点A，B，C，D分别表示有理数a，b，c，d，用“<”分别表示a，b，c，d，│a│，│b│，-│c│，-│d│．
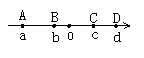
2．已知a>0，b<0，且│b│>│a│，在数轴上画出a，b的大致位置，并将a，b，-a，│b│用“>”连接起来．
3．有两上点，它们到原点的距离分别是2和3，问这两点之间的距离是多少？说明理由．
综合创新训练
四、学科内综合题
1．若a，b互为相反数，c和d互为倒数，m的绝对值是2，求
-cd+2│m│的值．
2．有理数a，b，c在数轴上的位置如图所示，若m=│a+b│-│b-1│-│a-c│-│1-c│，则100m的值是多少？
五、创新题
某汽车配件厂生产一批圆批的橡胶垫，从中抽取6件进行检验，比标准直径长的毫米数记作正数，比标准直径短的毫米数记作负数，检查记录如下：
| 1 | 2 | 3 | 4 | 5 | 6 |
| +0.5 | -0.3 | +0.1 | 0 | -0.1 | 0.2 |
（1）找出哪些零件的质量相对来讲好一些，怎样用学过的绝对值知识来说明这些零件的质量好；
（2）若规定与标准直径相差不大于0．2毫米为合格产品，则6件产品中有几件不合格产品．
六、竞赛题
设有理数在数轴上对应点如图所示，化简│b-a│+│a+c│+│c-b│．
中考题回顾
七、中考题
1．数轴上表示-的点到原点的距离是（ ）
A．-
B． C．-2
D．2
2．（2003·北京）-5的绝对值是（ ）
A．5
B．
C．- D．-5
3．（2002·河南）│-9│-5=_________．
4．（2002·山西）│-2│的相反数是________．
5．（2003·镇江）-的绝对值是________．
6．（2003·无锡）-2的绝对值是_________．
答案
一、1．D 2．B 3．D 4．C 5．C
二、1．2
0 2． -1．5 3．±3．1 ±1和0
4．±5
3 5．±7 9或5 6． -3．14 7．< < b-a
b-a 8．a≤0
9．（1）> （2）< （3）=
（4）>
三、1．a<-│d│<-│c│<b<│b│<c<d<│a│
2．图略 │b│>a>-a>b． 3．解：1或5，这两点可能在原点同侧，也可能在原点两侧，若在原点同侧这两点分别为2，3或-2，-3，它们之间的距离为1，若在原点两则，则这两点分别为-2，+3或-3，+2，它们之间的距离为5．
四、1．解：由题意得，a+b=0，cd=1，│m│=2，所以-cd+2│m│=0-1+4=3． 2．解：由图可知，a+b<0，b-1<0，a-c<0，1-c>0，m=-a-b-1+b-c+a-1+c=-2，则100m=-200．
五、解：（1）第3件、第4件、第5件的质量相对来讲好一些，比较记录数字的绝对值，绝对值越小越接近标准尺寸，所以绝对值较小的相对来讲好一些；（2）有2件产品不合格．
六、解：由图可知a>0，b<0，c<0，且有│c│>│a│>│b│>0，原式=（a-b）-（a+c）+（b-c）=-2c．
七、1．B 2．A 3．4 4．-2 5． 6．2