2.4 绝对值
一、课内训练:
1．求下列各数的绝对值．
（1）
； （2）-
； （3）-5；
（4）1； （5）0．
2．下列各组数中，互为相反数的是（ ）
A．-
与- B．-与-
C．-与 D．-与
3．计算：
（1）│-5│+│-2│；
（2）÷-；
（3）（
+-
+-1）×│-24│； （4）
．
4．（1）如果m=-1，那么-（-│m│）=________．
（2）若│a-b│=b-a，则a，b的大小关系是________．
5．若│a│=5，│b│=4，且a>0，b<0，则a=______，b=_______．
6．已知a、b、c三数在数轴的位置如图所示，化简
．
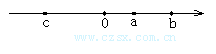
7．数a、b、c在数轴上对应的位置如图所示，化简：│a+c│-│a│+│b│．
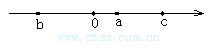
8．已知│a-3│+│2b+4│+│c-2│=0，求a+b+c的值．
9．某粮店出售三种品牌的面粉，袋上分别标有质量为（25±0.1）kg、（25±0.2）kg、（25±0.3）kg的字样，从中任意拿出2袋，它们的质量最多相差（ ）
A．0.8kg B．0.6kg C．0.5kg D．0.4kg
10．正式比赛时，乒乓球的尺寸要有严格的规定，已知四个乒乓球，超过规定的尺寸为正数，不足的尺寸记为负数，为选一个乒乓球用于比赛，裁判对这四个乒乓球进行了测量，得到结果：A球+0.2mm，B球-0.1mm，C球+0.3mm，D球-0.2mm，你认为应选哪一个乒乓球用于比赛？为什么？
二、课外演练
1．│-2│等于（ ）
A．-2 B．2 C．-
D．
2．绝对值为4的数是（ ）
A．±4 B．4 C．-4 D．2
3．-4的绝对值是________；2的相反数的绝对值是______．
4．若│a│=│-3│，则a=_______．
5．化简下列各数：
（1）-[-（-3）]； （2）-{-[+（-3）]}；
（3）-{+[-（+3）]}； （4）-{-[-（-│-3│）}．
6．下列推断正确的是（ ）
A．若│a│=│b│，则a=b B．若│a│=b，则a=b
C．若│m│=-n，则m=n D．若m=-n，则│m│=│n│
7．下列计算正确的是（ ）
A．--= B．
=± C．-（-3）=3 D．-│-6│=-6
8．若a与2互为相反数，则│a+2│等于（ ）
A．0 B．-2 C．2 D．4
9．已知│a-3│+│b-4│=0，求
的值．
10．绝对值大于2而小于5的所有正整数之和是（ ）
A．7 B．8 C．9 D．10
11．某车间生产一批圆形机器零件，从中抽6件进行检验，比规定直径长的毫米数记作正数，比规定直径短的毫米数记作负数，检查记录如下：
| 1 | 2 | 3 | 4 | 5 | 6 |
| +0.2 | -0.3 | -0.2 | +0.3 | +0.4 | -0.1 |
指出哪一个零件好些？怎样用学过的绝对值的知识来说明什么样的零件好些？
12．如图，在所给数轴上画出表示数-3，-1，│-2│的点．把这组数从小到大用“<”号连接起来．
答案：
一、课内训练:：
1．（1）││=；（2）│-│=；（3）│-5│=5；（4）│1│=1；
（5）│0│=0．
提示：根据绝对值的代数意义，判断其是正数、负数，还是零，然后再求出绝对值．
2．A
3．（1）│-5│+│-2│=5+2=7；
（2）÷-=÷=×=
；
（3）（+-+-1）×│-24│=（++
）×24=4+54+32=90；
（4）=
．
提示：利用绝对值的意义，先去掉绝对值，再计算．
4．（1）1 （2）a≤b
提示：（1）将m=-1代入-（-│m│）得-（-│-1│）=-（-1）=1；
（2）由│a-b│=b-a知，a-b与b-a互为相反数，那么a-b是负数或零，a-b≤0，
即a≤b，对于绝对值里含有字母的，要先考虑绝对值里代数式的正负，再去求绝对值．
5．5，-4
6．1 提示：│a│=a，│b│=b，│c│=-c．
7．c-b 提示：a+c>0，a>0，b>0．
8．5 提示：a-3=0，2b+4=0，c-2=0．
9．B 10．B球
二、课外演练
1．B
2．A 导解：绝对值等于一个正数的数有两个，它们互为相反数．
3．4 2
4．±3 导解：│-3│=3．
5．（1）-3；（2）-3，（3）3；（4）3．
6．D 导解：若两数相等或互为相反数，则这两数的绝对值相等；反之，若两数绝对值相等，则这两数相等或互为相反数．
7．D 8．A 导解：a+2=0．
9．解：由│a-3│+│b-4│=0，得a-3=0且b-4=0，所以a=3，b=4，=
．
10．A 导解：绝对值大于2，而小于5的正整数为3，4．
11．解：第六件零件好些；表中绝对值最小的那个零件好，因为绝对值越小，说明它与规定直径的偏差越小．
12．解：-3<-1<│-2│，如图．
