1.2 让我们来做数学
一、情境联想导入
随意写一个四位数，如1628，将它的四个数字从大到小排列得8621，再按从小到大排列得1268，用大数减去小数得7353．把7353按照上面的办法再做一遍；由大到小得7533；由小到大排列得3357，相减得4176．
问题 把4176再重复一遍，你会发现什么结论？
二、思维起点落实
1．在n×n的方案图案中，共有_______个正方形．
2．在做数学题时，特别是在数几何图形的个数时，要用_______、_______的方法．
三、重点难点突破
重点 体会做数学不是一个单纯的解题过程
学数学是一个复杂的过程．解数学题是学好数学的一个必要环节．解数学题，正确的方法是必不可少的，而掌握一种正确的方法要以独立思考为前提，逐渐形成“以我为主”的思考习惯．解数学题的过程实际上是充满观察、猜想、实验、类比、归纳、论证的探索过程，只要努力深入这一过程，就能探索出正确的方法．
点拨：“做数学”不仅包括做数学题，还包括搜集生活中的数学资料，进行数学实践，做数学游戏，发现并提出数学问题．掌握数学知识，发展数学思维，强化应用意识，形成良好数学品质也是“做数学”．“做数学”应理解为一切与数学有关的活动．
难点 积累生活经验，逐步渗透数学思想方法
在做数学题的过程中，实验、猜想是原来所不习惯的，不能总想套用公式和题目类型．这就要求同学们平时注意积累，掌握必要的数学思想方法，在观察的基础上，大胆进行归纳、猜想．
四、思维能力拓展
能力点 化归法在数学中的应用
例1 某城市共有2004名男、女乒乓球运动员分别参加男、女单打比赛，比赛采用淘汰制，最后分别产生男、女单打冠军．问：共需要安排多少场比赛？
分析：2004名运动员进行比赛，是一个具体的特殊问题，但是由于人数较多，解决起来并不容易．如何把这个问题变形，把它转化为容易解决的问题呢？不妨先考虑一般情形，探讨淘汰制比赛的一般规律．由于采用淘汰制，每赛一场，淘汰一名运动员；反过来考虑，要淘汰一名运动员，必须比赛一场；因为最后只剩男、女冠军各一人，所以共淘汰了（2004-2）人，即必须比赛（2004-2）场．于是，2004名运动员参加的比赛，需要安排2004-2=2002场．
答案：2002场．
拓展延伸：谋求一个问题的解决，可先把这个问题进行转化，使之转化为一个熟知的、易解决的问题，从而使原问题得以解决，“化归法”也是解数学问题常用的数学方法．
五、综合探究创新
综合点 数图形的个数
案例2 图中一共有多少个正方形？
分析：以一个单位长为边长的正方形有12个；以2个单位长为边长的正方形有6个；以3个单位长为边长的正方形有2个；所以共有20个正方形．
答案：20
评注：数图形个数时，要分类数．
六、针对训练
1．一串数1，1，1，2，2，3，4，5，7，9，12，16，21，…称为帕多瓦数列，请你陈述这个数的一个规律，并且写出其中的第14个数和第18个数．
2．完成下列计算：1+3=_____，1+3+5=_____，1+3+5+7=_____，1+3+5+7+9=______．根据计算结果猜想1+3+5+7+9+…+51=______．
3．育才中学七年级8个班进行足球友谊赛，比赛采用单循环赛制（参加比赛的队每两队之间只进行一场比赛），胜一场得3分，平一场得1分，负一场得0分．七（1）班积17分，并以不败战绩获得冠军，那么七（1）班共胜几场比赛？
4．在一条直线上有依次排列的9台机床在工作，现要设置一个零件供应站P，使这9台机床到供应站P的距离总和最小，P应设在何处．
5．上题中，如果有n台机床，其他不变，P点应设在何处？
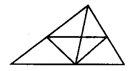
6．如图，图中有多少个三角形．
七、递进演练
1．商店出售下列形状的地砖：①正方形；②长方形；③正五边形；④正六边形．若只选购其中某一种地砖镶嵌地面，可供选择的地砖共有（ ）
A．1种 B．2种 C．3种 D．4种
2．某种细菌在培养过程中，细菌每半小时分裂一次（由一个分裂为两个），经过两小时这种细菌由一个可分裂繁殖成（ ）
A．4个 B．8个 C．16个 D．32个
3．在下列横线上填上确切的数．
（1）4，16，36，64，_____，144，196
（2）1，2，5，10，17，_____，37，50…
（3）2，6，18，______，162，486，______
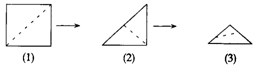
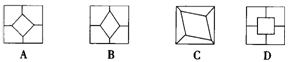
4．如图，小强拿一张正方形的纸，沿虚线对折一次得图（2），再对折一次得图（3），然后用剪刀沿图（3）中的虚线剪去一个角，再打开后的形状是（ ）
5．如图，在甲组图形的4个图形中，每个图是由4种基础图形A、B、C、D（不同的线段或圆）中的某两个图形组成的，例如由A、B组成的图形记为A·B，在乙组图形的a、b、c、d4个图形中，表示“A·D”和“A·C”的是（ ）
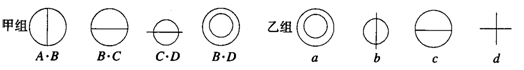
A．a，b B．b，c C．c，d D．b，d
6．把面值为10元的人民币换成零钱，现有足够的1元，2元和5元的人民币，则共有换法（ ）
A．4种 B．6种 C．8种 D．10种
7．从
+
+
+
+
+
中删去两个数，使得剩下的四个数之和恰好等于1，那么删去的两个数为（ ）
A．与 B．和 C．和
D．与
8．在2×3的方格图案中，如图所示，正方形和长方形的个数分别为（ ）
A．6个正方形，5个长方形 B．6个正方形，6个长方形
C．8个正方形，10个长方形 D．10个正方形，9个长方形
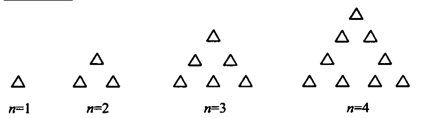
9．如图是用火柴棍摆出一系列三角形图案，按这种方式摆下去当底边上摆20（即n=20）根时，需要的火柴棍总数为______根．
10．计算:（1++
+）×（+++
）-（1++++）×（++）
11．已知4个矿泉水空瓶可换矿泉水一瓶，现在15个矿泉水空瓶，若不交钱，最多可以换几瓶矿泉水喝？
12．现有9棵树，把它们栽成3行，要使每行恰好为4棵，如图所示就是其中两种不同的栽法，请至少再给出3种不同栽法．
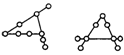
13．小明的爸爸买了一大盘铁丝，他想知道铁丝的长度，小明说：“把它拉直了一量不就知道了”．爸爸说：“不用那么费事，我有个简单的办法．”你知道小明的爸爸有什么好办法吗？
14．将四个相同的矩形（长是宽的3倍），用不同的方式拼成一个大矩形，拼得的大矩形的面积是四个小矩形的面积和，求有几种拼法．
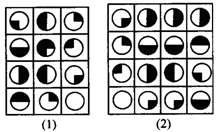
15．如图所示，图中每个图案代表一个阿拉伯数字，每横行三个符号自左至右看成一个三位数，这四层组成四个三位数，它们是837、571、206、439．按照图（1）中所示的规律写出图（2）中每一横行所表示的四位数分别是多少？
答案:
【情境联想导入】
会出现固定的数6174
【思维起点落实】
1×1+2×2+3×3+…+n×n
2．分类、观察
【针对训练】
1．这个数列有一条明显的规律：从第4项开始，第n项等于第n-2项与第n-3项之和（n≥4）．第14项是12+16=28．顺次可求出第15，16项是37，49．则第18项是37+49=86．
提示：通过观察发现：1+1=2；1+1=2；1+2=3；2+2=4；2+3=5；3+5=7…由此不难得解．
2．4 9 16 25 676
3．设七（1）班共胜x场，则平（7-x）场．
由题意得3x+1·（7-x）=17，解得x=5．
提示：8个班级进行单循环赛，其中每一个班都要与其他七个班各进行一场比赛，共计7场，而“不败”战绩的含义是：只有胜和平两种结果，而每个队的总积分=3分×战胜场次+1分×战平场次+0分×战负场次．
4．第5台处 提示：可先从2台、3台、4台……开始，找出一般规律．
5．当n为偶数时，P设在第
台和（+1）台之间的任一地方；当n为奇数时，P没在第
台位置．
6．13 提示：单个三角形6个，2个三角形合在一起4个，3个三角形合成三角形有2个，6个三角形合在一起的三角形有1个，所以共有6+4+2+1=13（个）．
【递进演练】
1．C 导解：①②④均可．
2．C 导解：2×2×2×2=16（个）．
3．（1）100 （2）26 （3）54 1458 导解：（1）为相应偶数自身乘积；（2）相邻两数差依次为1，3，5，7，…，17，…；（3）后一个数是前一个数的3倍．
4．C 导解：可通过动手操作得答案．
5．D 导解：观察甲组图形可得A表示一条竖直直线，B表示一个大圆，C表示一条水平直线，D表示一个小圆．
6．D 导解：全部换成2元有1种换法，全部换成1元的有1种换法，全部是5元的有一种，1元与2元混合的有4种换法，1元与5元混合有一种换法：1元、2元、5元混合的有2种换法，共有1+1+1+4+1+2=10．
7．D 导解：+++++
=（+++）++=
++=1++
8．C
9．630 导解：所用火柴棍依次为1，3，6，9，…，57，即求1+3+6+9+…+57．
10． 11．4
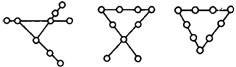
12．解：如图所示．
13．答：只需查出铁圈数，量出一圈的长度，二者相乘就可知道铁丝长度．
14．3种 导解：在拼图时要拼会，不要漏掉．
15.