有理数检测题(B)
|
一：选择题（每题2分，共20分）
1：数轴上表示整数的点称为整点，画一数轴规定单位长度为1厘米，若在这条数轴上随意画出一条长10厘米的线段AB，则线段AB盖住的整点有（ ）
A．8个或9个 B。9个或10个 C。10个或11个 D。11个或12个
2：在数轴上若点A到原点的距离为2个单位长度，则到点A的距离为3个单位长度且位于点A右侧的点表示什么数？（ ）
A．-1或5 B。-1或-5 C。1或-5 D。1或5
3：已知a与b互为相反数，则下列式子：①a+b=0，②a=-b，③b=-a，④a=b，⑤
，其中一定成立的是（ ）
A．1个 B。2个 C。3个 D。4个
4：一个数在数轴上所对应的点向右移动8个单位后，得到它的相反数，则这个数是（ ）
A．4 B。-4 C。8 D。-8
5：如果
，那么
和它的相反数的绝对值的和等于（ ）
A． B。0 C。-
D。-2
6：在数轴上，
，
，
对应的点如图所示，且
，
，则下列各式正确的是（ ）
A．
B。
C。
D。
7：π是（ ）
A整数 B分数 C有理数 D以上都不对
8：我国拟设计建造的长江三峡电站，估计总装机容量将达千瓦，用科学记数法表示总装机容量是（ ）
A 
千瓦 B
千瓦 C 
千瓦 D 
千瓦
9：1999年国家财政收入达到11377亿元，用四舍五入法保留两个有效数字的近似值为（ ）亿元
A 
B 
C 
D 
10：已知数
在数轴上对应的点在原点两侧，并且到原点的位置相等；数
是互为倒数，那么
的值等于（ ）
A 2 B –2 C 1 D –1
二、填空题（每题3分，共30分）
11：有理数中，是整数而不是正数的数是____________，是负数而不是分数的是__________。
12：比较大小：–π________–3.14（填=，＞，＜号＝。
13：________________________范围内的有理数经过四舍五入得到的近似数3.142。
14：如果
，则a=__________。
15：观察算式： 
，
，
…
按规律填空：
____________。
16：（2004·武汉）阳阳和明明玩上楼梯游戏，规定一步只能上一级或二级台阶，玩着玩着两人发现：当楼梯的台阶数为一级、二级、三级……逐步增加时，楼梯的上法数依次为1，2，3，5，8，13，21，…（这就是著名的裴波契数列），请你仔细观察这列数的规律后回答：
（1）上10级台阶共有_________种上法。
（2）这列数的前2003个数中共有_______________个偶数。
17：（2004·河南）观察下面一列数：-1，2，-3，4，-5，6，-7，…将这列数排成下列形式
按照上述规律排下去，那么第10行从左边数第9个数是_______；数-201是第_____行从左边数第__________个数。
18：（2004·云南）观察下列顺序排列的等式：
9×0+1=1，9×1+2=11，9×2+3=21，9×3+4=31，9×4+5=41……
猜想：第n个等式（n为正整数）用n表示，可以表示成_____________________。
19：数轴上原点右边4.8厘米处的点表示的有理数是32，那么，数轴左边18厘米处的点表示的有理数是____________。
20：已知
，则a是__________数；已知
，那么a是_________数。
三、解答题（70分）
21：（5分）请把下列有理数自定标准，恰当分类。
0，
，2，-7，3.15，
，
。
22：（共20分）计算下列各题（要求写出解题关键步骤）：
（1）（4分）
（2）（本题5分）
（3）（本题5分）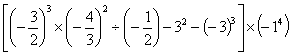
（4）（本题6分）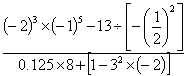
23：（6分）海边的一段堤岸高出海平面12米，附近的一建筑物高出海平面50米，海里一潜水艇在海平面下30米处，现以海边堤岸高度为基准，将其记为0米，那么附近建筑物及潜水艇的高度各应如何表示？
24：（6分）若m和n表示一对互为相反数，且m与n之间的距离是4.8，你能求出m和n这两个数吗？
25：（6分）已知a与b互为相反数，且b≠0。求a+b与
的值。
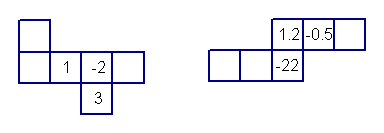
26：（8分）如下图是一个正方体纸盒的两个表面展开平面图，请在其余三个正方形内填入适当的数，使得折成正方体后，相对的面上的两个数互为相反数。
27：（9分）在抗击“非典”时期，某中学老师为减轻学生们的负担，让同学们做了一个游戏，他说：“如果张华和李明分别代表不大于5的正整数m、n，且
是最简真分数，那么形如
的数一共有多少个不同的有理数？”
28：（10分）如图是南宁冬季某一天的气温随时间变化的情况图，请你来观察：
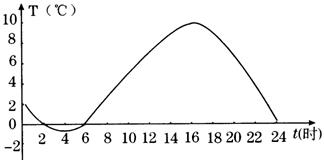（1）当天什么时间气温最低，最低气温是多少？
（2）当天什么时间气温最高，最高气温是多少？
（3）这一天的温差是多少？（结果都取整数）
有理数检测题(B)答案
一：选择题（每题2分，共20分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | C | D | C | B | B | A | D | C | A | B |
二：填空题（每题3分，共30分）
11：0和负整数，负整数； 12：＜ ； 13：大于或等于3.1415小于3.1425；
14：a=±1； 15：2500； 16：（1）：89，（2）：668； 17：90，15，5；
18：9（n-1）+n=10(n-1)+1； 19：-120； 20：0和正数，正数。
三、解答题（70分）
21：略； 22：（1）：-47，（2）：24，（3）：-30，（4）：3；
23：附近建筑物及潜水艇的高度各应为+38米、-42米；
24：m和n这两个数为2.4和-2.4；
25：a+b=0，
=-1；
26：-3，2，-1 ；-1.2，2.2，0.5。
27：形如的数一共有9个不同的有理数；
28：（1）当天4时气温最低，最低气温是约零下1℃；
（2）当天16时气温最高，最高气温是约10℃；
（3）这一天的温差是约11℃。