第2章 有理数 同步练习及单元检测
课标要求
1．通过具体情境的观察、思考、探索，理解有理数的概念，了解分类讨论思想；
2．借助数轴理解数形结合思想，学会用数轴比较数的大小，解决一些数学问题；
3．理解互为相反数的意义、绝对值的意义、倒数的意义，会进行与之有关的计算；
4．掌握有理数加、减、乘、除、乘方的法则，会进行加、减、乘、除及混合运算；
5．掌握科学记数法的意义及表示方法；
6．了解近似数及有效数字的意义，会按题目要求取近似数.
典型例题
在例题前，我们来了解一下本章的知识结构与要点.
例1 小红家、学校和小华家自东向西依次坐落在一条东西走向的大街上，小红家距学校
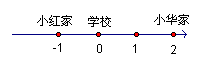分析：本题可借助数轴来解，如图所示，以学校为原点，学校以西为正方向，这样把实际问题转化为数学问题，观察数轴便可知此时小明的位置在小红家.
例2 若a与-7.2互为相反数，
则a的倒数是___________.
解：这道题既考察了相反数的概念，又考察了倒数的概念.
-7.2的相反数是7.2,所以a=7.2，a的倒数是
.
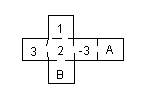例3 如图是一个正方体纸盒的展开图，在其中的四个正方形内分别标有1，2，3和-3，要在其余正方形内分别填上-1，-2，使得按虚线折成正方体后，相对面上的两数互为相反数，则A处应填_______.
解∶因为A的对面是2，所以正确答案是-2.
例4 已知有理数a,b满足条件a>0，b<0，a<b,
则下列关系正确的是（ ）.
A.-a<b<a<-b B.b<-a<a<-b C.-a<-b<b<a
D.b<-a<-b<a
解：这一题考察了绝对值的意义，和有理数大小比较，我们可借助数轴帮助解决问题，请同学们自己解答.
例5 计算–(+2.5)–(–41/4)+3.75–（+91/2）
解：原式=–2.5+4.25+3.75–9.5
=–(2.5+9.5)+(4.25+3.75)
=–12+8
=–4
说明：本题可以全部化成分数，通过通分来做；也可把所有整数部分相加，所有分数部分相加，最后在计算.
例6 如图：a , b , c在数轴上的位置如图所示，
试化简：︳a-b-
分析：本题考察的是绝对值的意义与运用，关键是如何判断绝对值里面数值的符号，从而去掉绝对值.
解：略
例7 2004年全年国内生产总值按可比价格计算，比上年增长9.5％,达到136515亿元.136515亿元用科学记数法表示（保留4个有效数字）为
A.1.365×1012元 B.1.3652×1013元 C.13.65×1012元 D.1.365×1013元
解：本题考察的是科学记数法和有效数字.
136515亿元=1.365×105亿元=1.365×1013元
注：科学记数法是把某一个数写成a×10n的形式，其中1≤a＜10,n为整数.
例8 计算：
（1）-5² (2)(- )³ （3）(-1)2005 （4）(-1 )²
解：本题考察乘方的意义和简单的乘方运算，应按照乘方的意义来进行运算，注意符号.
|
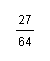-5²=-25 (- )³=-（ ） = -
 |
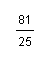(-1)2005 =-1 (-1 )²= （ ）2 =
 |
例9 （- ）-2-23×0.125+20040+-1
解：原式=4-8×0.125+1+1
=4-1+2
=5
例10 已知：a、b均为负数，c为正数，且b>a>c，化简.
解：依题意，画数轴、标出各数.
b-a<0, 所以得b<a<0<c, 且b+c<0 , a-c<0,
原式=│b+c│＋│a-c│＋│b-a│
＝-（b+c）-(a-c)-(b-a)
＝-2b
说明：通过构造数轴，将表示a、b、c的点标在数轴上后，便能直观地看出b+c<0 , a-c<0,b-a<0，再来化简代数式就不易出错了.
强化练习
一、填空题
1．甲、乙两厂三月产值与上月相比，甲厂增产3%，可记作________，乙厂减产1.2%,可记作_________.
2．将下列各数填在相应的表示数集的大括号内：
+3，-1，0.81，315，0，-3.14，-21/7，-12.9，+400%，+81/9，5.15115.
分数集∶｛ …｝
负数集∶｛ …｝
非负整数集∶｛ …｝.
3．1nm等于十亿分之
4．近似数2.428×105有______个有效数字，精确到_ ____位.
5．（–4）3=_______.
二、选择题
1．下列说法不正确的是 ( )
A.没有最大的有理数 B.没有最小的有理数 C.有最小的正有理数 D.有绝对值最小的有理数
2． 在数轴上表示-12的点与表示3的点，这两点间的距离为（ ）
A.9
B.
3. 若a的平方是4，则a的立方是( )
A.6
B
4． 如果ab>0,a+b<0,那么a,b的符号是( )
A.a>0,b>0 B.a>0, b<
三、计算题
1．
-1
-5
-1+3-4.5+2
2． 已知有理数a,b,c的和为0，且a=7,b=-2,则c为多少？
3．
2÷（-
）×
÷（-5
） 4．4-（-2）²-3÷(-1)³+0×(-2)³
5． （-1）2005+（-3）³×-
-（-4）³÷（-2）5
四、简答题
1．某企业生产瓶装食用调和油，根据质量要求，净含量（不含包装）可以有
2． 出租车司机小李某天下午的营运路线是在东西走向的一条大街上进行的，如果规定向东为正，向西为负，那么他这天下午行车的里程如下（单位：千米）：+16，-18，-3，+15，-11，+14，+10，+4，-12，-15.请回答下列问题：
(1)将最后一名乘客送到目的地时，小李距下午出车地点的距离是多少千米？
(2)如果汽车耗油量为a升/千米，则这天下午汽车共耗油多少升?
单元检测A卷
一、选择题
1．下列各式不正确的是（ ）
A．︱-2.4︱=︱2.4︱ B．(-3)4=
2. 如果一个有理数的平方是正数，那么这个有理数的立方是（ ）
A．正数 B．负数 C.非零数 D.非负数
3．计算（-1）2003+（-1）2003÷︱-1︱+（-1）2000的结果为（ ）
A.1
B．
4．数a,b,c在数轴上的位置如图所示，则a,b, -c由小到大的顺序是（ ）
A. a,-c,b B.b,a,-c C.a,b,-c D.b,-c,a
5．已知一个多位数的个位数字为m,且这个多位数的
任何次幂的个位数字仍为m,那么这个数字m( )
A.可能是0和1 B.只能是
6．下列说法错误的是（ ）
A.相反数与本身相等的数只有0 B.倒数与本身相等的数只有1和-1
C.平方与本身相等的数只有0和1 D.立方与本身相等的数只有0和1
7． 点A在数轴上距原点5个单位长度，将A点先向左移动2个单位长度，再向右移动6个单位长度，此时A点所表示的数是（ ）
A. –1
B
8． 若a+b<0,且ab<0,则（ ）
A.a,b同号 B. a,b异号 C.a,b都是负数 D.a,b都是正数
9． 如果一个数与它的相反数在数轴上对应点间的距离为8个单位长度，那么这个数是( )
A.+8和–8
B.+4和–
二、填空题
1．大于-5的负整数是_______________.
2．已知今天早晨的气温是–
3．已知一列按一定规律排列的数：–1，3，–5，7，–9，…，–17，19，如果从中任意选出若干个数相加，使它们的和为0，那么至少要选_______个数，请列出算式________(写出一个正确的即可)
4．若x,y满足︱2x-1︱+︱y+2︱=0,那么-x³+y²=__________.
5. 绝对值不小于3但小于6的负整数有_______个，他们分别是___________.
6．（1）若x²=x,则x=___ ； (2)若x³= x²,则x=____ ；
（3）若x³= x,则x=____.
7． 一根长50厘米的弹簧，一端固定，另一端挂上物体，在正常情况下，物体的质量每增加
三、解答题
1． 一货车司机小张某天上午的营运路线全部是在南北走向的向阳大街上进行的，如果规定向南为正，那么他在这天上午的行车路程如下（单位：千米）：+18,-15，+36，-48，-3.
（1） 上午停工时，小张在上午出车地点的什么位置上？
（2）若货车的耗油量为
2． 已知圆环的外圆半径为
3． 某厂的一个冷冻仓库的室温是
4． 用“<”号将下列各数连接起来，并求出它们的相反数和倒数.
 | | ||
2，0.3,-3, - , 3
5. 比较大小（填“＞”“=”或“＜”号＝
（1）1²+5²_______2×1×5；(2)(-2)²+3²____2×(-2)×3；
（3）(-4)²+(-4)²______2×(-4) ×(-4)
通过观察、归纳，探索出反映这一规律的一般结论，并用字母表示这一规律.
6． 已知a,b互为倒数，c,d互为相反数，且︱x︱=3，求2x²-（ab-c-d）+︱ab+3︱的值.
7． 计算
（1）-2³+(-2)²×(-1)-(-2)³÷(-2)² (2)- ×(- 1 )× ÷(-4)
| |
（3）-(-1)³-(-1 - )× ÷(-4)
单元检测B卷
一、填空题
1．绝对值大于1而小于4的整数是________
2．如果两个数互为相反数，那么它们的和等于_______；如果两个数互为倒数，那么它们的积等于_________.
3．通过测量得到某同学的身高是
4． 3745≈__________ (保留两个有效数字)；1.4105≈______（精确到千分位）.
5. ______的绝对值等于1.3,______的相反数等于0.
6. 四个互不相等的整数的积是9，那么这四个整数的和等于（ ）
A.27
B
二、计算题
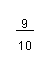
(1)(-9)-(-21)
（2）( - )+ (- )
（3）(-1 )×(- )÷
（4）(-1)+ (-1)² + (-1)³+(-1)4 + … +(-1)99+(-1)100+(-1)101
（5） ( 
+ 
- 
)÷(-24) （6）-99 
×9
三、问答题
1． 什么数等于它的倒数？什么数等于它的相反数？什么数等于它的绝对值？
2． 大于0而小于1的整数有没有？大于0而小于1的有理数有多少个？试写出十个这样的有理数.
3． 赵先生将甲、乙两种股票同时卖出，其中甲种股票进价是1000元，获利20%，一种股票进价也是1000元，获利-20%，则赵先生在这次买卖中是赚是赔？
4． 小红家春天粉刷房间，雇用了5个工人，干了10天完成；用了某种涂料
方案一：按工算，每个工30元；（1个工人干1天是一个工）
方案二：按涂料费用算，涂料费用的30%作为工钱；
方案三：按粉刷面积算，每平方米付工钱12元.
请你帮小红家出主意，选择方案________付钱最合算（最省）.
5． 草履虫可以吞噬细菌，使污水净化，一只草履虫每小时大约能够形成60个食物泡，每个食物泡中大约含有30个细菌，那么100只草履虫每天大约能够吞噬多少个细菌？（用科学记数法表示）.
6． 某超市对顾客进行优惠购物，规定如下：①若一次购物少于200元，则不予优惠；②若一次购物满200元，但不超过500元，按标价给予九折优惠；③若一次购物超过500元，其中500元以下部分(包括500元)给予九折优惠，超过500元部分给予8折优惠.小李两次去该超市购物，分别付款198元和554元，现在小张决定一次性地购买和小李分两次购买同样多的物品，他需付款多少元？
7． 我国宇航员杨利伟乘“神舟五号”绕地球飞行了14周，飞行轨道近似看作圆，其半径为6.71×10³千米，总航程约为多少千米？（π取3.14，保留3个有效数字）
第二单元参考答案
强化练习：一、1.+3%、-1.2% ； 2.略
二、.1.C 2. D 3. D 4. D 三、.1.-6.5 ；2.-5 ； 3.14/27 ； 4.3 ； 5.-9/2
四、1. 解:分别求出每个数的绝对值，将所求值与误差进行比较分析，小于或等于0.0021的为合格品，再合格品中再比较绝对值的大小，越小的质量越好。具体计算略。
2. 解：（1）∵+16-18-3+15-11+14+10+
（2）小李下午共走：16+18+3+15+11+14+10+4+12+15=118∴共耗油
单元检测A卷：一、1..C 2.C 3.B 4.B 5.A 6.D 7.C 8.B 9.B
二、1.-
6.略 7.(50+3x)
三、1．（！）. 解：+18-15+36-48-3 = -12 ；上午停工时，小张在出车地点的北
（2.）小张上午共走：+18+-15++36+-48+-3 =18+15+36+48+3=120（千米）
∴共耗油
2．解：S圆环 =π(402 –272 ) =871π
3．略 4.略 5.(1)> (2)> (3)= a² +b²≥2ab 6.21 7.(1)-10 (2)-3/40 (3)7/8
单元检测B卷：一、1.-2,-3,2,3 2.0 ,1 3_1.635≤h≤1.654 4. _3.75____×10³,1.411
5.±1.3 6.C
二、（1）12 ；（2）-7/6 ；（3）20/27 ；（4）-1 （5）-5/576
(6)-1799/2
三、1．略 2略
3．解：本题的关键是正确列出算式，卖价=进价×（1 + 利润率 ），所以甲种股票卖价为：
1000（1+20%）=1200（元） ；乙种股票卖价为：1000（1-20%）=800（元）。
所以卖价-进价=（1200+800）-（1000+1000）= 0
故赵先生在这次买卖中不赔不赚。
说明：这种实际应用题是中招考点，往往出现在选择题中。4。答案：方案二。
5．解：（60×30×24）×100 = = 4.32×106（个）
6．解：我们先算小李两次共买货物的价格：
554-500×90% = 104 104÷80% = 130
（1）假若198元的物品没打折 198+500+130 = 828
则小张购物828元需付的钱数：500×90%+（828-500）×80% = 721.4(元)
（2）假若198元的物品为扎九折 198÷90%=220
220+500+130=850 则小张购物850元的物品需付的钱数：
500×90%+（850-500）×80%=730（元） 你有简洁的算法吗？
7．解：2×6.71×10³π×14=2×6.71×10³×3.14×14≈5.90×105（千米）