3.1 代数式同步练习及单元检测
课标要求
1.掌握用字母表示数，建立符号意识.
2.会列代数式表示简单的数量关系，会正确书写代数式，会求代数式的值.
3.在数学活动中，体会抽象概括的数学思想方法和“特殊
一般”相互转化的辨证关系.
典型例题
例1 某市出租车收费标准为：起步价5元，3千米后每千米价1.2元，则乘坐出租车走x(x﹥3)千米应付______________元.
分析：因为x﹥3，所以应付费用分为两部分，一部分为起步价5元，另一部分为走（x-3）千米应付的1.2（x-3）元.
解：
注意：和、差形式的代数式要在单位前把代数式括起来.
例2 下列代数式中，书写正确的是（ ）
A. ab·2 B. a÷4 C. -4×a×b D. 
E. 
F. -3×6
分析：A：数字应写在字母前面 B：应写成分数形式，不用“÷”号 C：数与字母相乘，字母与字母相乘时，“×”号省略 D：带分数要写成假分数 E、F书写正确.
解：E、F.
例3 下列各题中，错误的是（ ）
A. 代数式
B. 代数式5(x+y)的意义是5与(x+y)的积
C. x 的5倍与y的和的一半，用代数式表示为
D. 比x的2倍多3的数，用代数式表示为2x+3
分析：选项C中运算顺序表达错误，应写成
友情提示：数学语言有文字语言、符号语言、图形语言.进行数学思维时，同学们要学会恰当使用各种语言推理分析，各种语言的互译是一种数学基本功.
例4 当x=1时，代数式
的值为2005，求x=－1时，代数式 的值.
分析：当x=1时，=
2005，p+q=2004,
当x=－1时，=－
－（p+q）+1=－2004+1=－2003.
解：当x=1时，=2005
p+q=2004
当x=－1时，=－
=－（p+q）+1=－2004+1 =－2003.
提示：“整体”思想在数学解题中经常用到，请同学们在解题时恰当使用.
例5 下图是一个数值转换机的示意图，请你用x、y表示输出结果，并求输入x的值为3，y的值为-2时的输出结果.
解：输出结果用x、y表示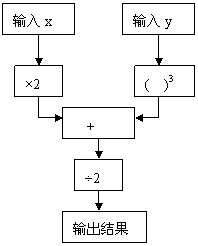
为：
当x=3,y=-2时,
=
=-1.
提示：把图形语言翻译为符号语言的关键是识图，
弄清图中运算顺序.
例6 某餐饮公司为大庆路沿街20户居民提供早餐方便，决定在路旁建立一个快餐店P，点P选在何处，才能使这20户居民到P点的距离总和最小？
分析：面对复杂的问题，应先把问题“退”到比较简单的情形：
如图1，如果沿街有2户居民，很明显点P设在p1、、、p2之间的任何地方都行.
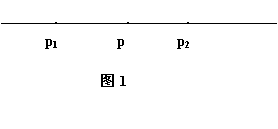
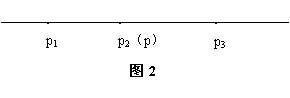
如图2，如果沿街有3户居民， 点P应设在中间那户居民、p2门前.
------
以此类推，沿街有4户居民，点P应设在第2、3户居民之间的任何位置，沿街有5户居民，点P应设在的第3户门前，------沿街有n户居民：当n为偶数时，点P应设在第
、
户居民之间的任何位置；当n为奇数时，点P应设在第
户门前.
解：根据以上分析，当n=20时，点P应设在第10、11户居民之间的任何位置.
思维驿站： 请同学们认真体会“特殊一般”的辨证关系，掌握化归的思想方法，学会把复杂的问题化为简单的情形来解决.
强化练习
一、填空题
1. 代数式2a-b表示的意义是_____________________________.
2. 列代数式：⑴设某数为x,则比某数大20%的数为_______________.
⑵a、b两数的和的平方与它们差的平方和________________.
3. 有一棵树苗，刚栽下去时，树高2.1米，以后每年长0.3米，则n年后的树高为________________，计算10年后的树高为_________米.
4. 某音像社对外出租光盘的收费方法是：每张光盘在出租后的头两天每天收0.8元，以后每天收0.5元，那么一张光盘在出租后第n天（n＞2的自然数）应收租金_________________________元.
5. 观察下列各式：12+1=1×2，22+2=2×3，32+3=3×4------
请你将猜想到的规律用自然数n(n≥1)表示出来______________________.
6. 一个两位数，个位上的数是a，十位上的数字比个位上的数小3，这个两位数为_________，当a=5时，这个两位数为_________.
二、选择题
1. 某品牌的彩电降价30%以后，每台售价为a元，则该品牌彩电每台原价为（ ）
A. 0.7a元
B.0.3a元 C.
元
D. 
元
2. 根据下列条件列出的代数式，错误的是（ ）
A. a、b两数的平方差为a2-b2 B. a与b两数差的平方为(a-b)2
C. a与b的平方的差为a2-b2 D. a与b的差的平方为(a-b)2
3. 如果
那么代数式(a+b)2005的值为（ ）
A. –2005 B. 2005 C. -1 D. 1
4. 笔记本每本m元，圆珠笔每支n元，买x本笔记本和y支圆珠笔，共需（ ）
A. （ mx+ny）元 B. (m+n)(x+y) C. （nx+my ）元 D. mn(x+y) 元
5. 当x=-2,y=3时,代数式4x3-2y2的值为（ ）
A. 14 B. –50 C. –14 D. 50
三、解答题
1.
已知代数式3a2-2a+6的值为8, 求
的值.
2.
当a=-1,b=-
,c=
时，求代数式b2-4ac的值，并指出求得的这个值是哪些数的平方.
3. 人在运动时的心跳速率通常和人的年龄有关.如果用a表示一个人的年龄，用b表示正常情况下这个人在运动时所能承受的每分钟心跳的最高次数，那么b=0.8(220-a).
⑴ 正常情况下,在运动时一个14岁的少年所能承受的每分钟心跳的最高次数是多少？
⑵ 一个45岁的人运动时10秒心跳的次数为22次，请问他有危险吗？为什么？
单元检测
一、填空题（每小题5分，共25分）
1. 某机关原有工作人员m人，现精简机构，减少20%的工作人员，则剩下_____人.
2. 结合生活经验作出具体解释：a-b__________________________________.
3. 甲以a千米/小时、乙以b千米/小时（a＞b）的速度沿同一方向前进，甲在乙的后面8千米处开始追乙，则甲追上乙需_____________小时.
4. 若梯形的上底为a，下底为b，高为h，则梯形的面积为____________;当a=2cm，b=4cm，h=3cm时，梯形的面积为____________.
5. 按下列程序计算x=3时的结果__________.
|
|
|
|
二、选择题（每小题5分，共25分）
1. 下列式子中符合代数式的书写格式的是（ ）
A. x·
B.
C.
D.
2. 一个长方形的周长是45cm，一边长acm，这个长方形的面积为（ ）cm2
A.
B.
C.
D.
3. 代数式x2-7y2用语言叙述为（ ）
A.x与7y的平方差 B.x的平方减7的差乘以y的平方
C.x与7y的差的平方 D. x的平方与y的平方的7倍的差
4. 当a=-2,b=4时，代数式
的值是（ ）
A.56 B.48 C. –72 D.72
5. 一个正方体的表面积为54 cm2，它的体积是（ ）cm3
A.
27
B.9
C.
D. 36
三、解答题（每题10分，共50分）
1. 列代数式
⑴ 若一个两位数十位上的数是a，个位上的数是b，这个两位数是_________.
若一个三位数百位上的数为a,十位上的数是b，个位上的数c，这个三位数是_________.
⑵ 某品牌服装以a元购进，加20%作为标价.由于服装销路不好，按标价的八五折出售，降价后的售价是__________元，这时仍获利________________________元.
⑶电影院第一排有a个座位，后面每排比前一排多2个座位，则第x排的座位有____________个.
⑷A、B两地相距s千米，某人计划a小时到达，如果需要提前2小时到达，每小时需多走___________________千米.
2. 已知代数式
的值为7，求代数式
的值.
3. 当
时，求代数式
的值.
4. 若
，求
的值.
5. 给出下列程序：
若输入x=1时，输出的值为-2，求输入x=-2时，输出的值是多少？
强化练习参考答案
一、1.2a与b的差 2.⑴(1+10%)x ⑵(a+b)2 +(a-b)2 3. 2.1+0.3n 5.1 4.1.6+0.5(n-2) 5.n2+n=n(n+1) 6.10(a-3)+a 25 二、1.D 2.C3.C 4.A 5.B
三、1. ∵3a2-2a
+6=8
2. b2-4ac=(-)2-4×(-1)×
=
∴ 3a2-2a=2
∵(±
)2=
∴
∴是±的平方.
∴
3. ⑴b=0.8(220-14)=164.8
答：正常情况下,在运动时一个14岁的少年所能承受的每分钟心跳的最高次数164次.
⑵b=0.8(220-45)=140, ∵22×6=132 132＜140 ∴他没有危险.
单元检测参考答案
一、１．(1-20%)m
2．答案不唯一 ３．
４．
，9cm2 ５．15
二、１C ２D ３B ４C ５A
三、1．⑴ 10a+b,100a+10b+c ⑵ (1+20%)a·85%,0.2a ⑶
a+(x-1) ⑷ (
) ２．19
３．-3.5 ４. -5 ５．4.