七年级数学相交线测试
一、判断
1.顶点相同并且相等的两个角是对顶角.( )
2.相交直线构成的四个角中若有一个角是直角,就称这两条直线互相垂直.( )
3.直线外一点到这条直线的垂线段叫做这点到这条直线的距离.( )
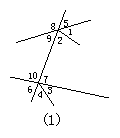
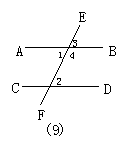
4.如图1,∠2和∠8是对顶角.( )
5.如图1,∠2和∠4是同位角.( )
6.如图1,∠1和∠3是同位角.( )
7.如图1,∠9和∠10是同旁内角,∠1和∠7也是同旁内角.( )
8.如图1,∠2和∠10是内错角.( )
9.O是直线AB上一点,D分别在AB的两侧,且∠DOB=∠AOC,
则C,O,D三点在同一条直线上.( )
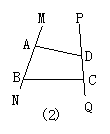
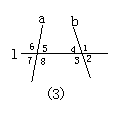
10.如图2,其中共有4对同位角,4对内错角,4对同旁内角.( )
二、填空
11.如图3,直线L截直线a,b所得的同位角有______对,它们是______;内错有___对,它们是______;同旁内角有______对,它们是______;对顶角_____对,它们是_______.
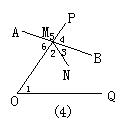
12.如图4,∠1的同位角是________,∠1的内错角是________,∠1的同旁内角是_______.
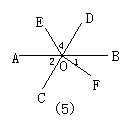
13.如图5,直线AB,CD相交于O,OE平分∠AOD,FO⊥OD于O,∠1=40°,则∠2=_____,∠4=______.
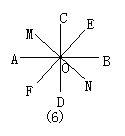
14.如图6,AB⊥CD于O,EF为过点O的直线,MN平分∠AOC,若∠EON=100°,那么
∠EOB=_____,∠BOM=_____.
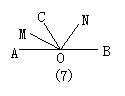
15.如图7,AB是一直线,OM为∠AOC的角平分线,ON为∠BOC的角平分线,则OM,ON的位置关系是_______.
16.直线外一点与直线上各点连结的线段中,以_________为最短.
17.从直线外一点到这条直线的________叫做这点到直线的距离.
18.经过直线外或直线上一点,有且只有______直线与已知直线垂直.
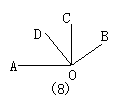
19.如图8,要证BO⊥OD,请完善证明过程,并在括号内填上相应依据:∵AO⊥CO,∴∠AOC=__________(___________).又∵∠COD=40°(已知),∴∠AOD=_______.∵∠BOC=∠AOD=50°(已知),∴∠BOD=_______,∴_______⊥_______(__________).
20.如图9,直线AB,CD被EF所截,∠1=∠2,要证∠2+∠4=180°,请完善证明过程,并在括号内填上相应依据.∵直线AB与EF相交,∴∠1=∠3=(__________),又∵∠1+∠4=180°(___________),∠1=∠2(已知),∴∠2=∠3,∠2+∠4=180°(____________________)
三、选择.
21.下列语句正确的是( )
A.相等的角为对顶角 B.不相等的角一定不是对顶角
C.不是对顶角的角都不相等
D.有公共顶点且和为180°的两个角为邻补角
22.两条相交直线与另外一条直线在同一平面内,它们的交点个数是( )
A.1 B.2 C.3或2 D.1或2或3
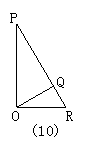
23.如图10,PO⊥OR,OQ⊥PR,能表示点到直线(或线段)的距离的线段有( )
A.1条 B.2条 C.3条 D.5条
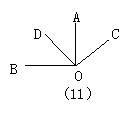
24.如图,OA⊥OB,OC⊥OD,则( )
A.∠AOC=∠AOD B.∠AOD=∠DOB C.∠AOC=∠BOD D.以上结论都不对
25.下列说法正确的是( )
A.在同一平面内,过已知直线外一点作这条直线的垂线有且只有一条
B.连结直线外一点和直线上任一点,使这条线段垂直于已知直线
C.作出点P到直线的距离
D.连结直线外一点和直线上任一点的线段长是点到直线的距离
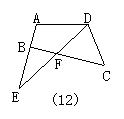
26.如图12,与∠C是同旁内角的有( ).
A.2 B.3 C.4 D.5
27.下列说法正确的是( ).
A.两条直线相交成四个角,如果有三个角相等,那么这两条直线垂直.
B.两条直线相交成四个角,如果有两个角相等,那么这两条直线垂直.
C.两条直线相交成四个角,如果有一对对顶角互余,那么这两条直线垂直.
D.两条直线相交成四个角,如果有两个角互补,那么这两条直线垂直.
28.如果∠1与∠2互为补角,且∠1>∠2,那么∠2的余角是( )
A. 
(∠1+∠2) B. ∠1 C. (∠1-∠2) D.∠2
29.已知OA⊥OC,∠AOB:∠AOC=2:3,则∠BOC的度数是( )
A.30° B.150° C.30°或150° D.以上答案都不对
四、解答.
30.如图,已知∠ABC=90°,∠1=∠2,∠DCA=∠CAB,求证:(1)CD⊥CB;(2)CD平分∠ACE.
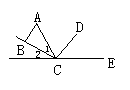
31.如图,已知AO⊥OB于O,∠2-∠1=20°,求∠1,∠2的度数.
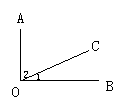
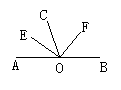
32.如图,OE,OF分别是∠AOC与∠BOC的平分线,且OE⊥OF,求证:A,O,B三点在同一直线上.
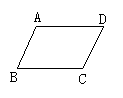
33.如图,按要求作出:(1)AE⊥BC于E;(2)AF⊥CD于F;(3)连结BC,作AG⊥BD于G.
答案:
一、1.× 2.∨ 3.× 4.× 5.∨ 6.× 7.× 8.∨ 9.∨ 10.×
二、11.4∠1和∠5,∠4和∠6,∠7和∠3,∠8和∠22,∠5和∠3,∠4和∠82, ∠4和∠5,∠3 和∠84,∠1和∠3,∠2和∠4,∠5和∠7,∠6和∠8
12.∠4和∠NMP ∠6 ∠2和∠BMO
13.50° 65° 14.55°135° 15.垂直 16.垂线段 17.垂线段的长度 18.一条 19.90° 垂直的性质 50°90° BO OD 垂直的定义
20.对顶角相等平角的定义等量代换
三、21.B 22.D 23.D 24.C 25.A 26.C 27.A 28.C 29.C
四、30.(1)证明:∵∠ABC=90°,
∴∠1+∠CAB=90°.
又∵∠DCA=∠CAB,
∴∠DCA+∠1=90°,即∠BCD=90°,
∴CD⊥CB.
(2)∵∠1+∠2+∠ACD+∠DCE=180°,
又∵∠1+∠ACD=90°,
∴∠2+∠DCE=90°.
又∵∠1=∠2,
∴∠ACD=∠DCE,
∴CD平分∠ACE.
31.∠1=35°,∠2=55°.
32.(略) 33.(略)