七年级数学角测试题
一、判断
1.所有的直角都相等.( ) 2.大于直角的角都是钝角.( )
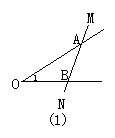3.如图1,∠1也可以用∠AOB或∠O来表示.( )
4.由同一端点出发的两条直线组成的图形叫做角.( )
5.一个锐角和一个钝角的和等于一个平角.( )
6.一个角的补角大于这个角.( )
7.一个钝角减去一个锐角必然得到一个锐角.( )
8.一个角的补角减去这个角的余角是一个直角.( )
9.同角或等角的余角相等,补角也相等.( )
10.若有一个公共顶点和一条公共边的两个角互补,
则这两个角的另一边必在同一直线上.( )
11.120.5°=120°50′.( ) 12.42°51′÷3+16°29′×4=80°13′.( )
二、填空.
13.角是有公共端点的两条_______组成的图形,也可以看成是由一条______绕它的端点旋转而成的图形._______叫做角的顶点,_______叫做角的始边,_______叫做角的终边.
14.1周角=______°,1平角=______°.
15.18.32°=18°( )′( )″,216°42′=_______°.
16.若一个角的余角是这个角的4倍,则这个角是_______,这个角的补角是______.
17.互为补角的两个角可以都是_______角,或者一个是______角,一个是____角.(填“钝角”、“锐角”、“直角”)
18.两个角的和等于________(
),就说这两个角互为余角;两个角的和等于________( ),就说这两个角互为补角.
19.已知∠1=43°27′,则∠1的余角是_______,补角是________.
20.从一个角的顶点引出的一条_______,把这个角分成两
个相等的角,这条______叫做这个角的_______.
21.如果两个角是对顶角,那么这两个角_______.
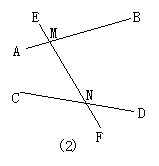
22.如图2,∠AME的补角是_______,对顶角是_______.
23.计算:8°43′50″-18°43′26″×5-37°3′÷3=_________.
24.计算:180°-52°18′36″-25°36″×4=____________.
25.若时钟表示的时间为5点15分时,时钟的时针和分针所成的锐角是_____°.
26.在∠AOB的内部引出OC,OD两条射线,则图中共有______个角,它们分别是_________.
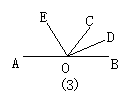
27.如图3,∠BOC=60°,OE,OD分别为∠AOC,∠BOC的角平分线,则∠EOD=_______,∠COE=_______,∠BOE的角平分线是_______.
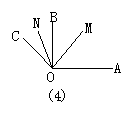
28.如图4,OM,ON平分∠AOB和∠BOC,∠MON=60°,那么∠AOC=_____,∠BOC=_____.
29.角α的补角是它的余角的4倍,则角α=_______.
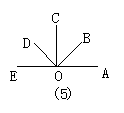
30.如图5,已知∠COE=∠BOD=∠AOC=90°,则图中与∠BOC相等的角为_______,与∠BOC互补的角为_______,与∠BOC互余的角为________.
三、选择
31.下列各角中,( )是钝角.
A.
周角 B.
周角 C.平角 D.平角
32.两个锐角的和( )
A.必定是锐角 B.必定是钝角
C.必定是直角 D.可能是锐角,可能是直角,也可能是钝角
33.互为补角的两个角的比是3:2,则这两个角是( )
A.108°,72° B.95°,85° C.100°,80° D.120°,60°
34.如果两个角的和等于180°,那么这两个角一定是( ).
A.两个锐角; B.两个直角; C.一个锐角,一个钝角; D.两个直角或一个锐角,一个钝角
35.已知OC平分∠AOB,则下列各式:(1)∠AOC=
∠AOB;(2)∠AOC=∠COB;(3)∠AOB=2∠AOC,其中正确的是( )
A.只有(1) B.只有(1)(2) C.只有(2)(3) D.(1)(2)(3)
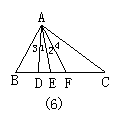
36.如图6,已知∠1=∠2,∠3=∠4,则下列结论正确的个数为( ).
(1)AD平分∠BAF;(2)AF平分∠DAC;(3)AE平分∠DAF;(4)AE平分∠BAC.
A.1 B.2 C.3 D.4
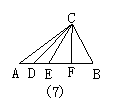
37.如图7,以C为顶点的角(小于平角)共有( ).
A.4个 B.8个 C.10个 D.18个
38.已知∠AOB=30°,∠BOC=80°,∠AOC=50°,则下列说法正确的是( )
A.射线OB在△AOC内 B.射线OB在△AOC外
C.射线OB与射线OA重合 D.射线OB与射线OC重合
39.已知∠MON=30°,∠NOP=15°,则∠MOP=( ).
A.45° B.15° C.45°或15° D.无法确定
40.用一副三角板的内角(其中一个三角板的内角是45°,45°,90°,另一个是30°,60°,90°)可以画出大于0°且小于176°的不同度数的角共有( )
A.8种 B.9种
C.10种 D.11种
四、计算
41.如图,已知∠AOB:∠BOC=3:5,又OD,OE分别是∠AOB和
∠BOC的平分线,若∠DOE=60°,求∠AOB和∠BOC的度数.
42.已知∠AOB=45°,∠BOC=30°,求∠AOC的度数.
43.如图,已知OB平分∠AOC,且∠2:∠3:∠4=2:5:3,求∠1,∠2,∠3,∠4的度数.
44.若一个角的补角是这个角余角的3倍,那么这个角是多少度?
45.以∠AOB的顶点O为端点射线OC,使∠AOC:∠BOC=5:4.(1)若∠AOB=18°,求∠AOC与∠BOC的度数;(2)若∠AOB=m°,求∠AOC与∠BOC的度数.
五、证明
46.如图,已知∠ABC=∠ACB,∠1=∠2,∠3=∠4,求证:∠2=∠4.
47.已知角α的余角为β,β的补角是α的4倍,求证: α=β
六、作图.
48.用三角板画出下列图形:(1)画∠AOB=105°;(2)以OB为始边,在∠AOB内部画∠AOC=15°.(保留作图痕迹,并写出作法)
七、辨析
49.判断“顶点相同,且角相等的两个角是对顶角”是否正确,并说明理由.
答案:
一、1.∨ 2.× 3.∨ 4.× 5.× 6.× 7.× 8.∨ 9.∨ 10.∨ 11.× 12.∨
二、13.射线 射线 射线的端点 起始位置的射线 终止位置的射线
14.360 180 15.19122 16.716.18°162° 17.直钝锐 18.90°直角180°平角19.46°33′136°33′ 20.射线射线角平分线 21.相等 22.∠AMF和∠EMB∠FMB 23.90° 24.27°39′ 25.67.5 26.6∠AOC,∠AOD,∠AOB,∠COD,∠COB,∠BOD 27.90°60°OC 28.120°30° 29.60° 30.∠DOE∠AOD∠COD和∠AOB
三、31.C 32.D 33.A 34.D 35.D 36.B 37.C 38.B 39.C 40.D
四、41.∠AOB=45°,∠BOC=75°.
42.∠AOC=75°或∠AOC=15°.
43.∠1=∠2=60°,∠3=150°,∠4=90°.
44.45°.
45.(1)第一种情形:OB在△AOC的内部,
可设∠AOC=5x,∠BOC=4x,
则∠AOB=x,即x=18°.
∴∠AOC=90°,∠BOC=72°.
第二种情形:OB在△AOC的内部,
可设∠AOC=5x,∠BOC=4x,
则∠AOB=∠AOC+∠BOC=9x,
∴9x=18°,即x=2°.
∴∠AOC=10°,∠BOC=8°.
(2)∠AOC=5m°,∠BOC=4m°.或∠AOC=
m°,∠BOC=
m°.
五、
46.证明:∵∠1=∠2,
∴∠2=∠ABC,
∵∠3=∠4,
∴∠4=∠ACB,
又∵∠ABC=∠ACB,
∴∠2=∠4.
47.(略)
六、48.(略)
七、49.这句话是不正确的,
如答图所示,
∠AOC=∠BOC,且有共同顶点,
但∠AOC,∠BOC不是对顶角.