4.6 角
一、选择题
1．下列说法正确的是（ ）
（A） 角的两边可以度量; (B)角是由两条射线构成的图形．
(C)一条直线可以看成是一个平角; (D)平角的两边可以看成直线．
2．下列说法不正确的是（ ）
（A） 两个锐角的和不一定大于直角; (B)两个钝角的和不一定大于平角．
(C)只有锐角才有余角; (D)任何小于平角的角都有补角．
3．从∠AOB的顶点O引出两条射线OC、OD两条射线，图中共有角的个数为（ ）
（A）4个． （B）5个． （C）6个． （D）7个．
４．下列各角中，是钝角的为（ ）
（A）
． （B）
． （C）
． （D）
．
 |
５．如图，共有（ ）个小于平角的角．
（A）5． （B）6． （C）7． （D）8．
|
6．用一副三角板的内角可以画出大于0º且小于180º的不同角度的角共有（ ）
（A）9种． （B）10种． （C）11种． （D）12种．
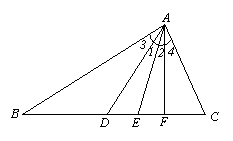
7．如图，已知∠1=∠2，∠3=∠4，则下列结论正确的个数为（ ）
①AD平分∠BAF．
②AF平分∠DAC．
③AE平分∠DAF． ④AE平分∠BAC．
（A）1． （B）2． （C）3． （D）4．
8．∠A与∠B互补，∠B与∠C互余，则∠A一定是（ ）
（A）锐角． （B）钝角． （C）直角． （D）不能确定．
9．八点三十分，这一时刻，时针与分针夹角是（ ）
（A）70°． （B）75°． （C）80°． （D）85°．
二、填空题
10．角是由有 的两条射线组成的图形，两条射线的 是这个角的顶点，角也可以看成是由一条射线 ．
11．1个周角= 个平角= 个直角．
12．当时钟的时间为6:30分时,时针与分针的夹角为 度．
13．从8点10分到8点40分,时钟的时针转过 度,时钟的分针转过 度．
14．108°42ˊ= 度；35.28°= 度 分 秒.
15．13°39ˊ+64°45ˊ= ．
16．图中共有 角,以点A为顶点的角是 .
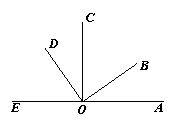
B
(第16题图) (第17题图)
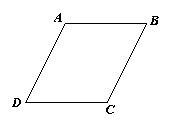
17．如图,已知∠COE=∠BOD=∠AOC=90°,则图中互余的角有 对,互补的角有 对.
18．如图,A,B,C分别代表学校、图书馆、小红家，学校和图书馆分别在小红家的北偏西方向，学校又在图书馆的北偏东方向，那么图中点A表示 ，点B表示 ，点C表示 .
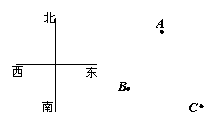
（第18题图） (第20题图)
19．如果车站在学校的北偏东10千米处,那么学校在车站的 方向 处．
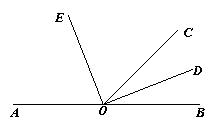
20．如图,∠BOC=60°,OE、OD分别为∠AOC和∠BOC的平分线,则∠EOD= ,
∠COE= ,∠BOE的平分线是 ．
三、解答题
21．计算：
①
②
③
④
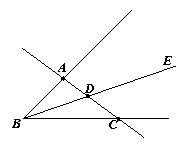22．如图,以B为顶点的角共有几个?请把它们写出来,以D为顶点的角呢?
23．如果在∠AOD的内部从顶点O引出2条射线,求图中有多少个角?如果引出3条射线呢?如果引出100条射线呢?你发现了什么规律?
24．已知一个角的补角比这个角的余角的三倍还多20°,求这个角．
25．在图中画出:
(1)表示北偏东30°的射线OA；
(2)表示东南方向的射线OB；
(3)表示南偏西方向60°的射线OC．
26．如图，∠AOC与∠BOD都是直角,且∠AOB:∠AOD=2:11.求∠AOB与∠BOC的度数.
D C
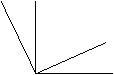
B
O A
27．在平面上,∠AOB=100°,∠BOC=60°,若OM平分∠AOB,ON平分∠BOC,求∠MON的度数．
28．小刚星期天早晨8:00出发去奶奶家,中午11:30返回.他出发时和返回时时钟的时针和分针夹角各是多少?时针转过的角度是多少?
答案:
一、1.D 2.B 3.C 4.C 5.C 6.C 7.B 8.B 9.B
二、10.公共端点 公共端点 绕端点旋转而得到的图形 11.2 4
12.15° 13.15° 180° 14.108.7° 
15.78°24ˊ 16. 8 ∠A 17. 4,5 18.学校 图书馆 小红家
19.南偏西 10千米 20.90° 60° 射线OC
三、21.①69°10ˊ②187°15ˊ③30°47ˊ ④23°20ˊ
22.3个 ∠ABE ∠ABC ∠EBC 4个 ∠ADE ∠ADB ∠BDC ∠CDE
23.6个 10个 5151 24.55° 25.略
26. 20°, 70° 27. 80°或 20° 28.120° 165° 105°
课题：4.6 角 讲学槁
学习目标：
1、认识互为余角和补角概念，理解互为余角和补角主要反映角的数量关系。
2、认识对顶角的概念，理解对顶角主要反映了角的一种位置关系。
预习要求：认真预习课本p157—p158和创新目标手册p127—p129
预习自测：
1、两个角的和等于 ，就说这两个角互为 ，简称 。
2．两个角的和等于 ，就说这两个角 ，简称 。
3．同角或等角的余角 ，同角或等角的补角 ，对顶角 。
4．判断：
①若∠1+∠2+∠3=180°, 则∠1,∠2,∠3互补。-----------------------（ ）
②任何角都有余角。----------------------------------------------------------（ ）
③若两个角相等，则这两个角是对顶角。-------------------------------（ ）
④一个角的补角一定比这个角大。----------------------------------------（ ）
⑤两个角的补角相等，那么这两个角也相等。-------------------------（ ）
尝试探讨一：
1． 已知 ∠
=60°18′，求∠的余角和补角。
 |
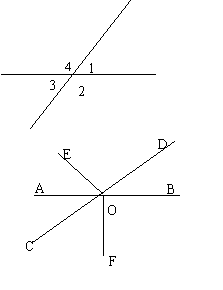2． 在图中，∠1=50°,那么∠2、∠3和∠4各等于多少度？
尝试探讨二：
1． 锐角∠=x°，则∠的余角为
，
∠的补角为 ，补角与余角的差为 。
2． 如图，直线AB、CD相交与点O，OE、OF是过点O的
射线，其中对顶角有 。
3． 一个角等于它的补角的2倍，求这个角的补角的余角。
尝试探讨二：1.两条直线相交有几对对顶角？
2．三条直线相交有几对对顶角？
3．四条直线相交有几对对顶角？
4．n条直线相交有几对对顶角？
课堂训练
1． 判断：
① 90°的角叫做余角。--------------------------------------------------------（ ）
② 如果∠1是∠2的补角，那么∠1一定是钝角。----------------------（ ）
③ 如果∠1是∠2的余角，那么∠1一定是锐角。----------------------（ ）
④ 若两个角的顶点相同，则这两个角是对顶角-------------------------（ ）
⑤若∠1﹤∠2，则∠1的补角也小于∠2的补角-------------------------（ ）
2．一个角的补角比这个角的余角大 °
3．若∠1与∠2是对顶角，则∠1与∠2的大小关系是 。
4．若∠1+∠2=90°，∠1+∠3=90°，则∠2与∠3的大小关系是 ，其理由是 。
5．若∠1+∠2=180°，∠3+∠4=180°，且∠1=∠3，则∠2与∠4的大小关系是 ，其理由是 。
6．已知∠A与∠B互补，且∠A﹕∠B=7﹕2，求∠A与∠B的大小。
7．一个角的余角与这个角的补角互补，求这个角。
8．一个角的余角与这个角的补角的和比平角的
多1°，求这个角。
9．如图，∠ACB=90°，∠CDB=90°，
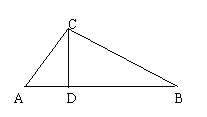（1）与∠A互余的角有
；
（2）与∠B互余的角有 ；
（3）与∠A相等的角有 ；
（4）与∠B相等的角有 ；
10．一个角的补角比它的余角的2倍还大20度，
求这个角。