《数据的收集与整理》最新考点例析
河北 李凤君
2006年各课改实验区对数据的收集与整理的考查，主要集中在以下几个方面：
考点一、调查方式的合理选择
对于一项调查工作，是应该用全面调查还是抽样调查，应根据具体情况确定．
例1（江苏淮安）下列调查方式，合适的是【 】
A．要了解一批灯泡的使用寿命，采用普查方式；
B．要了解淮安电视台“有事报道”栏目的收视率，采用普查方式；
C．要保证“神舟六号”载人飞船成功发射，对重要零部件的检查采用抽查方式；
D．要了解外地游客对“淮扬菜美食文化节”的满意度，采用抽查方式．
分析：一般来说，如果数据的收集比较容易或者需要非常精确，则用全面调查，否则用抽样调查．对所有灯泡都测试寿命、获得收看某电视栏目的所有观众数或者对一次大型活动满意的所有人数都是不容易做到，也不必做的，这些都使用抽样调查；对于像“神舟六号”载人飞船的重要零部件是一件极为重要的事情，不允许有任何疏漏，必须全部检查，所以要采用全面调查的方式．
由以上分析可知，应选D．
考点二、数据处理的相关概念
目前阶段，我们所学的与数据处理相关的概念主要有总体、样本、平均数等．
例2（江苏泰州）下列说法正确的是【 】
A．为了了解我市今年夏季冷饮市场冰淇淋的质量可采用普查的调查方式进行；
B．为了了解一本300页的书稿的错别字的个数，应采用普查的调查方式进行；
C．销售某种品牌的鞋，销售商最感兴趣的是所销售的的平均数；
D．为了了解我市九年级学生中考数学成绩，从所有考生的试卷中抽取1000份试卷进行统计分析，在这个问题中，样本是被抽取的1000名学生．
分析：本例既有对调查方式的考查，又有对基本概念的考查．
用普查方式了解全市今年夏季冷饮市场冰淇淋的质量不现实；对一本书的错别字则可以逐页逐个地查找，即采用普查的调查方式是正确的．
销售商最感兴趣的哪种尺码的鞋销量大，而平均数并不是他们最感关心的．
“总体”和“样本”这两个概念，都是针对调查对象而言的，这里的调查对象最终反映为数据，表达的句子中心词应该是数据，而不能是事物或人．比如在D中，“总体”和“样本”应该是指数学成绩，而不是学生．所以，样本是被抽取的1000名学生的数学成绩．
总之，应选B．
考点三、数据处理的综合应用
数据处理具有极强的实用性，在实际应用时往往和其他知识相联系，共同解决某一问题．
例2（江苏苏州）今年，苏州市政府的一项实事工程就是由政府投人1 000万元资金．对城区4万户家庭的老式水龙头和13升抽水马桶进行免费改造．某社区为配合政府完成该项工作，对社区内1200户家庭中的120户进行了随机抽样调查，并汇总成下表：
| 改造 情况 | 均不 改造 | 改造水龙头 | 改造马桶 | ||||
| 1个 | 2个 | 3个 | 4个 | 1个 | 2个 | ||
| 户数 | 20 | 31 | 28 | 21 | 12 | 69 | 2 |
(1)试估计该社区需要对水龙头、马桶进行改造的家庭共有＿＿＿＿＿户；
(2)改造后，一只水龙头一年大约可节省5吨水，一只马桶一年大约可节省15吨水．试估计该社区一年共可节约多少吨自来水?
(3)在抽样的120户家庭中，既要改造水龙头又要改造马桶的家庭共有多少户?
分析：本例体现了用样本估计总体思想在实际问题中的具体应用．
(1)在抽查的120户中，均不改造的20户，另外的100户需要对水龙头、马桶进行改造．照此比例，估计该社区1200户家庭中需要对水龙头、马桶进行改造的家庭户数为
．
(2)抽样的120户家庭一年共可节约用水：
（1×31+2×28+×21+4×12）× 5+(1×69+2×2)×15 =198×5＋73×15=2085(吨)．
所以，该社区一年共可节约用水的吨数为
2085×
=20850(吨)．
(3)设既要改造水龙头又要改造马桶的家庭共有x户，则只改造水龙头不改造马桶的家庭共有(92一x)户，只改造马桶不改造水龙头的家庭共有(71一x)户，根据题意列方程，得
x+(92一x)+(71一x)=100，
解得
x=63．
所以，既要改造水龙头又要改造马桶的家庭共有63户．
也可以从另一角度考虑，从表中数据可以看出，在这120户中，改造水龙头和改造马桶的户数之和为
31+28+21+12+69+2=163（户）．
由于只有100户需要对水龙头、马桶进行改造，所以多出的就是既要改造水龙头又要改造马桶的家庭．因此，此类家庭的人数为
163-100=63（户）．
例1（2005年大连市）为了了解某初中学生的体能情况，抽取若干名学生在单位时间内进行引体向上测试，将所得数据整理后，画出统计图（如图1），图中从左到右依次为第1、2、3、4、5组.
（1）求抽取多少名学生参加测试？
（2）处于哪个次数段的学生数最多？（答出是第几组即可）
（3）若次数在5次（含5次）以上为达标，求这次测试的达标率.
解析：（1）抽取的学生人数为：
10＋25＋35＋25＋5=100；
（2）由统计图知，第5组学生数最多；
（3）由统计图知，本次测试次数在5次（含5次）以上的人数为：35＋25＋5=65，所以这次测试的达标率为：
×100%=65%.
2、扇形统计图能清晰地展现出各部分在总体中所占的百分比
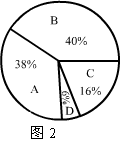
例2（2005年安徽）某校九年级(1)班有50名同学, 综合数值评价”运动与健康”方面的等级统计如图所示, 则该班”运动与健康”评价等级为A的人数是______.
解析：由扇形统计图知，该班”运动与健康”评价等级为A的人数占全班人数38%，所以该班”运动与健康”评价等级为A的人数是：50×38%=19（名）.
3、折线统计图能清晰地展现出事物变化的情形
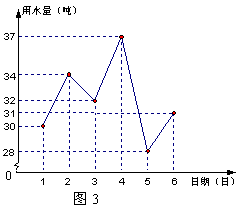
例3（2005年浙江省）某住宅小区六月份中1日至6日每天用水量变化情况如图所示，那么这6天的平均用水量是（ ）
A、30吨；B、31吨；C、32吨；Ｄ、33吨.
解析：由折线统计图知，这6天的平均用水量为：
（30＋34＋32＋37＋28＋31）=×192=32（吨）.故应选C.
4、统计图的综合运用
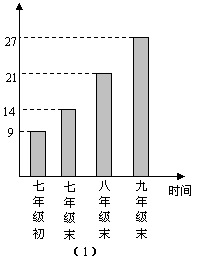
例4（2005年陕西）某校对某班45名学生初中三年中戴近视眼镜人数进行了跟踪调查，统计数据如图4（1）所示.
 |
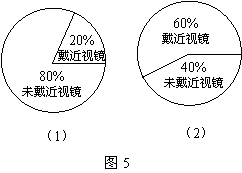
（1）如果用整个圆代表该班人数，请在图4（2）圆中画出该班七年级初戴近视眼镜人数和未戴近视眼镜人数的扇形统计图，并标出百分比；
（2）如果用整个圆代表该班人数，请在图4（3）圆中画出该班九年级末戴近视眼镜人数和未戴近视眼镜人数的扇形统计图，并标出百分比；
（3）今年，我省某区约有8000名九年级学生，如果这些学生中戴近视眼镜人数的百分率与这个班九年级末戴近视眼镜人数的百分率基本相同，请估计这8000名学生中戴近视眼镜的人数大约是多少？
解析：（1）根据条形统计图中所提供的数据，可得该班七年级初戴近视眼镜人数的百分比：
×100%=20%，即未戴近视眼镜人数的百分比：1－20%=80%.
根据上面数据可画出扇形统计图，如图5（1）所示.
（2）根据条形统计图中所提供的数据，可得该班九年级末戴近视眼镜人数的百分比：
×100%=60%，即未戴近视眼镜人数的百分比：1－60%=40%.
根据上面数据可画出扇形统计图，如图5（2）所示.
 | |||
| |||
（3）由题意，得
8000×60%=4800（名）.