第二章 相交线平行线练习
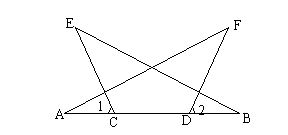
1. 如图，已知：CE=DF，AC=BD，
1=2。求证：A=B。
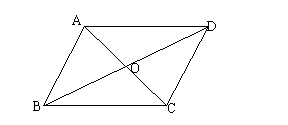
2. 如图，已知：AB//CD，AB=CD，求证：AC与BD互相平分。
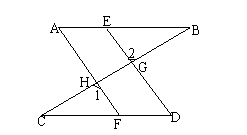
3. 已知：如图，E、F分别是AB和CD上的点，DE、AF分别交BC于G、H，A=D，1=2，求证：B=C。
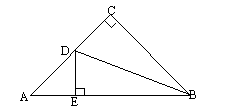
4. 已知：如图，在
中，
，AC=BC，BD平分CBA，
于E，求证：AD+DE=BE。
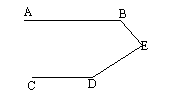
5. 如图，已知：AB//CD，求证：B+D+BED=
（至少用三种方法）
【试题答案】
1. 证明：
2. 证明：
即AC与BD互相平分。
3. 证明：
又
4. 证明：
在
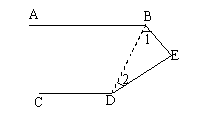
5. 证明：（1）连结BD。
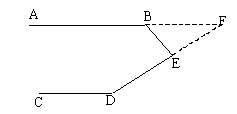
（2）延长DE交AB延长线于F。
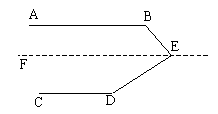
（3）过点E作EF//AB，
