1.4 从不同方向看
一.填空题
1. 我们从不同的方向观察同一物体时,可能看到不同的图形,其中,把从正面看到的图叫做_____________,从左面看到的图叫做__________,从上面看到的图叫做_______________.
2. 主视图,左视图和俯视图都一样的几何体有________(写出一种即可).
3. 圆柱的俯视图是_______,主视图是_________.
4. 正方体的俯视图是____________,圆锥的主视图是_______________.
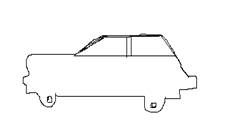
5. 有一辆小汽车如图1-15,小红从空中往下看这辆小汽车,图____是小红看到的形状.


![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
 (1)
(2)
(3)
(1)
(2)
(3)
二. 选择题
6. 如图1-16所示,甲,乙,丙三个侦察员,从三个不同方位观察一间房子,哪个图形是侦察员甲看到的( )
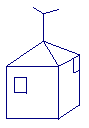

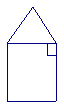

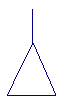
图1-16 A B C D
7. 从正面看图1-17,所能看到的结果是图形( )
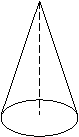


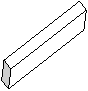 | |||
![]()
图1-17 A B
![]()
![]()
C D
8. 图1-18所示的粮仓的俯视图是( )
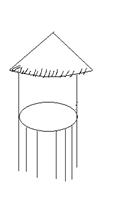
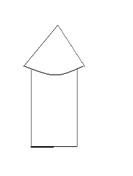
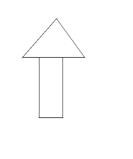
图1-18 A B

C D
9. 下面说法中错误的是( )
A. 球的主视图是圆 B. 球的俯视图是圆
C. 球的任何截面都是圆 D. 以上说法都不对
三. 解答题
10. 画出图1-20所示几何体的主视图,左视图与俯视图.
 | 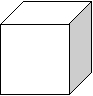 | ||
(1) 图1-20 (2)
11. 如图1-21,这是一个由小立方块搭成的几何体的俯视图,小正方形中得数字表示在该位置的小立方块的个数,请你画出它的主视图与左视图.
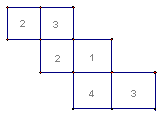
12. 一个几何体的主视图,左视图和俯视图如图1-22.
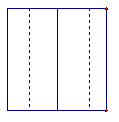
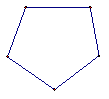
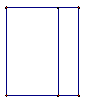
主视图 俯视图 左视图
请想一想这是一个什么样的几何体?有可能请画一个草图表示.
13. 一个几何体的俯视图如图1-23,想一想它是一个什么样的几何体,请画出一个草图表示.

图1-23
14. 画出如图1-24所示几何体的主视图,左视图和俯视图.
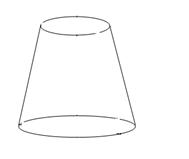
图1-24
同步练习拓展从不同的方向看
(一)下面画的是我们日常生活中常见的几件用具,只是它们都是从某一个方向观察到的图形,你能分别说出它们是什么东西吗?
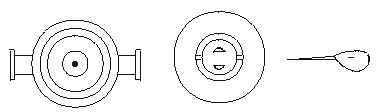
解:根据题意,这几个物体都是从正上方看到的,它们是(1)铝锅;(2)白炽灯泡;(3)菜刀.
(二)巧剪零件
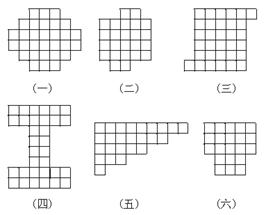
图1
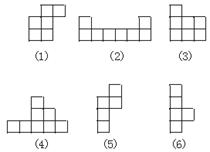
图2
某工厂有六种规格的铜片,其形状如图1所示.现分别要剪图2那样六种形状的零件,如果每一种铜片都只能剪某一种形状的零件,那么应该如何搭配才能充分利用材料,使剪完后铜片的边角料一点也不剩余?
由于六种规格的铜片和六种形状的零件都是由小方格组成的,所以一种铜片能够剪成某种零件而没有边角料的必要条件,是铜片的小方格的总数应为这一零件中小方格块数的倍数.六种铜片的小方格总数分别为:
| (一) | (二) | (三) | (四) | (五) | (六) |
| 30 | 24 | 32 | 32 | 25 | 21 |
六种零件的小方格块数分别为:
| (1) | (2) | (3) | (4) | (5) | (6) |
| 6 | 8 | 7 | 8 | 5 | 6 |
对照表中的数据,按照上面提出的倍数关系,以及铜片和零件在形状上的特点,稍加分析,就可以获得下列几种剪法:
第(一)块铜片剪(5)号零件,第(二)块铜片剪(1)号零件,第(三)块铜片剪第(4)号零件,第(四)块铜片剪第(2)号零件,第(五)块铜片剪第(6)号零件,第(六)块铜片剪第(3)号零件.