2.3～2.5 阶段性复习
一、阶段性内容回顾
1．只有符号不同的两个数称为_______，0的相反数是______．
2．表示互为相反数的两个点位于原点的_______，并且与原点的距离______．
3．多重符号的化简：“＋”号可以省略；若“－”号为偶数个，就是_______；若“－”号为奇数个，变为原数的________．
4．我们把在数轴上表示数a的点与原点的距离叫做数a的________，记做_______．
5．│a│=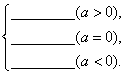
6．两个负数比较，绝对值大的________．
7．正数________负数，正数______0，0_________负数．
8．若│x│+│y│=0，则x=_______，y=________．
二、阶段性巩固训练
1．+3.2的相反数是________；-3的相反数是________，0的相反数是_______；+（-6）的相反数是________；-（-6）的相反数是________．
2．若a，b互为相反数，x，y互为倒数，则（a+b）·
-xy=________．
3．已知x>3，化简│x-3│为______．
4．若│x-5│=0，则x=_______；若│x+5│=5，则x=______．
5．将-
，│-2│，-│
│，-2.5，│-2.5│用“<”号连接起来：___________．
6．绝对值不小于2且不大于5的整数有_______个，其和为________．
7．│x-1│+│x+2│的最小值为_______．
8．若-1<x<0，下列结论
>x，│-x│>1，x<-x中，正确的个数是（ ）．
A．1 B．2 C．3 D．没有
9．若1<x<4，则
=（
）．
A．2 B．-2 C．0 D．0或±2
10．化简下列各式：
（1）-[-（+3）]；（2）-[-（+0.05）]；（3）-{-[+（-3
）]}；（4）-[-（x-y）]．
11．已知│x-2│+│y+1│=0，求│x│+y的值．
12．（1）观察下面的一列数，在横线上写出符合其排列规律的数．
-1，，-
，
，-
，
，______，______，…，_____，（第1000个数），…
（2）如果上面的这列数按其规律无限地排列下去，它会越来越接近一个数，这
个数是_________，但永远也不会等于这个数．
13．某摩托车配件厂生产了一批圆形的像胶垫，从中抽取6件进行检验，比标准直径长
的毫米数记做正数，比标准直径短的毫米数记做负数，记录如下：
| 1 | 2 | 3 | 4 | 5 | 6 |
| +0.3 | -0.1 | +0.1 | 0 | -0.3 | +0.2 |
（1）指出哪个零件的质量好一些（即质量最接近规定的质量）；
（2）若规定与标准直径相差不大于0.2mm为合格产品，则6件产品中有几件不合格产品？
14．已知│a│=3，│b│=3，│c│=5，且a，b，c在数轴上的位置如图所示，求a+b+c的值．
15．有理数a，b，c的大小关系如图所示，试比较下列各组数的大小．
（1）-a，-b，-c （2）a+2，b+2，c+2
16．某股民上星期五买进某公司的股票1000股，每股27元，下表为本周内每日该股票
的涨跌情况（单位：元）：
（1）星期三收盘时，每股多少元？
（2）本周内每股的最高价为多少元？最低价为多少元？
（3）已知买进股票时须付成交额1.5‰的手续费，卖出时还须付成交额1.5‰的手续费
和1‰的交易税，如果他在星期四收盘前将全部股票卖出，那么他的收益情况如何？
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 每股涨跌 | +4 | +4.5 | -1 | -2.5 | -4 |
答案：
【阶段性内容回顾】
1．相反数 0 2．两侧 相等 3．原数 相反数
4．绝对值 │a│ 5．a 0 -a 6．反而小
7．大于 大于 大于 8．0 0
【阶段性巩固训练】
1．-3．2 3 0 6 -6
2．-1 点拨：a+b=0，xy=1．
3．x-3 点拨：x-y>0．
4．5 0或-10 点拨：∵│x+5│=5，∴x+5=±5，∴x=0或-10．
5．-││<-2.5<-<│-2│<│-2.5│
6．8 0
7．3 点拨：当-2≤x≤1时，│x-1│+│x+2│取最小值，原式=1-x+x+2=3．
8．A 点拨：只有x<-x正确．
9．C 点拨：原式=
=-1+1=0．
10．（1）3 （2）0.05
（3）-3 （4）x-y
11．∵│x-2│≥0，│y+1│≥0，│x-2│+│y+1│=0，
∴x-2=0，y+1=0，
∴x=2，y=-1．
∴│x│+y=│2│+（-1）=1．
12．（1）-
（2）0
13．（1）第4件 （2）有2件不合格产品．
14．∵│a│=3，│b│=3，│c│=5，
∴a=±3，b=±3，c=±5．
由图可知a>0，b>0，c>0，
∴a=3，b=-3，c=5．
∴a+b+c=3+（-3）+5=5．
15．（1）-a>-b>-c （2）a+2<b+2<c+2
16．（1）27+4+4.5-1=34.5（元）；
（2）最高价：27+4+4.5=35.5（元）；
最低价：27+4+4.5-1-2.5-4=28（元）．
（3）股价为27+4+4.5-1-2.5=32（元），
32×（1-1.5‰-1‰）×1000-27×（1+1.5‰）×1000=4879.5（元）．