七年级数学上学期半期试题（人教版）
（考试时间120分钟，满分150分）
一.填空题.(每小题3分,共48分)
1.
= .
2.合并同类项:
= .
3.若
互为相反数,
互为倒数,则
=
.
4.某超市进了一批商品,每件进价为
元,相对于进价,若要获利25%,则每件商品的零售价
应定为 元。
5.若代数式
的值是3,则代数式
的值是 .
6.如果x=0是关于x的方程3x-2m=4的解，则m的值为： 。
7.下午2点的时候,时针与分针成的夹角是 度.
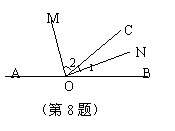
8.如图,A、O、B三点在一条直线上,OM是∠AOC的角平分线.ON是∠BOC的角平分线,
若∠1:∠2= 1:2,则∠1= 度。
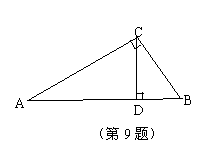9.若α+β=90°，则α与β互余。如图,直角三角形ABC中,∠ACB=90º,CD⊥AB.则图中互余的角的对数是
.
 | |||||
 | |||||
| |||||
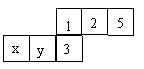10.解方程
得:
=
.
11.如图,要使平面图折叠成正方体后相对面上的两数和相等.则
= .
12.定义运算
,且
,则
=
.
13.已知:
则
= .
14.
º ′.
15.渝怀铁路重庆段列车从重庆出发到秀山县,运行途中停靠的车站依次是重庆→长寿→涪陵→武隆→彭水→黔江→酉阳→秀山,则重庆段内需要安排不同的火车票有 种.
16.若
,则
的末位数字是 .
二.选择题.(每小题3分,共30分)
1.下列运算正确的是( )
A.
B.
C.
D.
2.如果有理数满足
,
,则下列说法正确的是( )
A.
B.
C.
D.
3.若
,如
的值为( )
A.
B.
C.3
D.不确定
4.由几个相同的小正方体搭成的几何体的视图如下,则搭成这个几何
体的小正方体的个数是(
)
A.4 B.5
|
|
|
5.若
,那么( )
A.
B.
C.
D.为任意有理数
6.平面内有三个点,过任意两点画一条直线,则可以画直线的条数是( )
A.2条 B.3条 C.4条 D.1条或3条
7.如果A、B、C三点在一条直线上,A到B的距离是4cm,B到C的距离是7cm,那么A、C两点三间的距离是( )
A.3cm B.11cm C.3cm或11cm D.无法确定
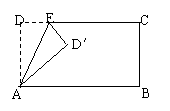8.将长方形的纸ABCD沿AE折叠,得到如图
所示的图形,已知∠CED′=60º.则∠AED的是( )
A.60º B.50º
C.75º D.55º
9.已知
,那么代数式
的值是( )
A.2004
B.
C.2005
D.
10.有一串数,
按一定的规律排列,那么这串数中前( )个数的和最小.
A.500 B.501 C.502 D.503
三.解答题.(每小题6分，共42分)
1.计算
2.合并同类项:
3.先化简,再求值:
.其中
.
4.解方程:
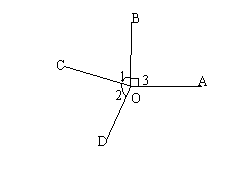5.如图:OB⊥OA,OC是∠BOD的平分线,若∠1:∠3=7:9.求∠BOD的度数.
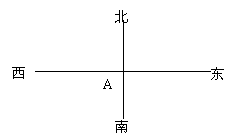
6.作图题:在小岛A处的北偏东60º距离小岛60千米的B处有一台风中心.设台风中心正沿南偏西30度的方向运动.若离台风中心35千米范围内的地方都要受台同的影响.问:小岛是否受台风影响? 请作图后回答.(作图时10千米画1cm)
 |
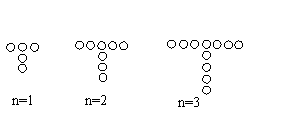
7.观察规律:
|
|
请你将规律用含自然数n
的式子表示出来.
四.解答题.(共30分)
1.
(共7分)已知线段AB,延长AB到C,使BC=
AB.D为AC的中点,若DC=4cm,求AB的值.
2. (共7分)大利区每台电脑电话拨号上网有两种方式.用户可任选其一:
(A)计时制:3元/时； (B)包月制:60元/月。 此外:每种上网方式都得加收通信费2元/时。
(1)某用户用一台电脑某月上网的时间为小时,请你分别写出两种收费方式下该用户应该支付的费用;
(2)该用户每月上网多少小时,两种方式的费用一样?
(3)若某用户估计一月的上网时间是30小时,你认为哪种方式划算?
3. (共7分)某市出租车的收费标准是:起步价5元(即行驶距离不超过3km都需付5元车费).超过3km时,每增加1km,加收1.8元(不足1km按1km计).某同学 坐这种出租车从甲地到乙地,其支付车费19.4元,则此人从甲地到乙地经过的路程的最远值可能是多少?
4. （9分）（1）如图，已知点C在线段AB上，且AC=6cm,BC=4cm,点M、N分别是AC、BC的中点，求线段MN的长度；
（2）在（1）中，如果AC=acm，BC=bcm,其他条件不变，请猜出MN的长度；
（3）对于（1），如果我们这样叙述它：已知线段AC=6cm，BC=4cm,点C在直线AB上，点M、N分别是AC、BC的中点，求MN的长度。结果会变化吗？如果变化，求出结果。
 |
七年级数学半期试题答案
一.填空题.(每小题3分,共48分)
1. 2. 
3.
4.
5.1 6.
7.60
8.30
9.4
10.
11.7
12.4007
13. 7 14.66, 42 15.56 16.7
二.选择题.(每小题3分,共30分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | C | C | A | B | C | D | C | A | B | B |
三.解答题.(每小题6分，共42分)
1.解:原式
(4分)
(5分)
(6分)
2.解:原式
(3分)
(3分)
3.解:原式
(2分)
(3分)
(4分)
当
, 
时,
原式
(5分)
(6分)
4.解:去括号,得:
(2分)
移项,得:
(4分)
合并同类项得:
(5分)
两边同时除以5,得:
(6分)
5.解:设∠1=
∠3=
∵OB⊥OA ∴∠AOB=90º
(1分)
∴∠3==90º ∴=10º
(3分)
∴∠1==
º=70º
(4分)
又∵OC是∠BOD的平分线, ∴∠1=∠2 ∴∠2=70º (5分)
∵∠BOD=∠1+∠2 ∴∠BOD=70º+70º=140º (6分)
解法二:∵OB⊥OA ∴∠3=90º (1分)
∵∠1:∠3=7:9 ∴∠1=70º (4分)
∵OC是∠BOD的平分线, ∴∠BOD=2∠1=
º=140º
(6分)
6.解:∵图上AC=3cm ∴AC的实际距离是
千米
(5分)
∵30千米<35千米
∴小岛要受到台风的影响 (6分)
7.
(1分)
(3分)
|
（3分）
四.1.解:∵D是AC的中点 ∴AC=2DC ∵DC=4cm ∴AC=
=8cm (3分)
设BC=,则AB=
∵AB+BC=AC ∴
(5分)
∴
(6分)
∴
∴AB=6cm
(7分)
2.解:①A计时制收费:
(1分)
包月制收费:
(2分)
(2)∵两种方式的费用一样
∴
(3分)
∴
∴ 
(4分)
当该用户每月上网20个小时,两种方式的费用一样.
(3)当
时:
A:计时收费
元.
B:包月制收费:
元
∵150>120 ∴B包月制划算 (7分)
3.解:设此人从甲地到乙地经过的路程的最远值是千米
(1分)
(4分)
解这个方程:
10<路程
11
(6分)
答: 此人从甲地到乙地经过的路程的最远值是11千米.
解法二:
(元)
(2分)
(千米)
(4分)
8+3=11(千米) (6分)
答: 此人从甲地到乙地经过的路程的最远值是11千米. (7分)
4.解:(1)∵M是AC的中点 ∴MC=
AC ∵AC=6cm ∴MC=3cm
∵N是BC的中点 ∴CN=BC ∵BC=4cm ∴CN=2cm
∴MN=MC+CN=5cm (3分)
(2)方法同上:MN=
cm
(5分)
(3)有变化:当点B在线段AC的延长线上时,MN=5cm(解法见1) (6分)
当点B在线段AC内时:
∵M是AC的中点 ∴MC=AC=
6=3cm
∵N是BC的中点 ∴CN=BC=
=2cm
∴MN=MC-CN=3-2=1cm (9分)