七年级数学上学期竞赛试题

七年级数学上学期竞赛试题

一、选择题(每小题4分，共40分)

　 1、如果m是大于1的偶数，那么m一定小于它的…………………………..　 　　　　 （　 　）

A、相反数　　　　　　　　　　 B、倒数　　　　　　　　　 C、绝对值　　 　 D、平方　

2、当ｘ＝－2时， 的值为9，则当ｘ＝2时，的值是（　 　）　 　  A、－23　　　　 B、－17　　　　　C、23　　　　 D、17

3、2，3，5，6这四个数中最小的数是………………………………..　  （　 　）

A. 2　　　　 　 B. 3　　　　　 C. 5　　　　D. 6

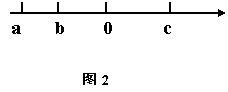
4、把14个棱长为1的正方体，在地面上堆叠成如图1所示的立体，然后将露出的表面部分染成红色．那么红色部分的面积为　　　　 ……………………………..　　　（　 　）．

A、21 　　　　　 B、24　　　　　　C、33 　　　　 D、37

5、有理数的大小关系如图2所示，则下列式子中一定成立的是…… （　 　）

A、＞0　 B、　　 C、 D、

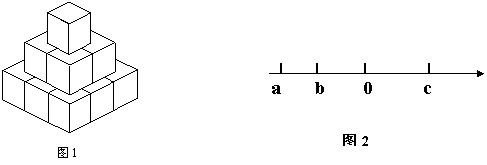
6、某商场国庆期间举行优惠销售活动，采取“满一百元送二十元，并且连环赠送”的酬宾方式，即顾客每消费满100元（100元可以是现金，也可以是购物券，或二者合计）就送20元购物券，满200元就送40元购物券，依次类推，现有一位顾客第一次就用了16000元购物，并用所得购物券继续购物，那么他购回的商品大约相当于打　　　　　　 （　 　）。

A、９折　　　　　B、8.5折 　　　 C、８折　　　　　 　D、7.5折

7、如果有2005名学生排成一列，按1、2、3、4、3、2、1、2、3、4、3、2、1……的规律报数，那么第2005名学生所报的数是………………………………………………………………　　　（　 　）

A、1　　 　　　　 B、2　　 　　　　 C、3　　  　　　　　　　D、4

8、 方程 x=ax+1有一负根而无正根, 则a的取值范围……………………　　（　 　）

A. a>－1　　　　 B. a>1　　　　  C. a≥－1　　　　　  D. a≥1

9、的最小值是……………………………………………………　（　 　）

A. 5　　　　　　 B.4　　　　　　C.3　　　　　　　　　 D. 2

10、某动物园有老虎和狮子，老虎的数量是狮子的2倍。每只老虎每天吃肉4.5千克，每只狮子每天吃肉3.5千克，那么该动物园的虎、狮平均每天吃肉…… …… 　　（　 　）

A、 千克　 　 B、 千克　　C、千克 　　　 D、千克

二、填空题(每小题5分，共40分)

11、定义a*b=ab+a+b,若3*x=27，则x的值是_____。

12、三个有理数ａ、ｂ、ｃ之积是负数，其和是正数，当x＝时，则。

13、当整数m＝_________ 时，代数式的值是整数。

14、A、B、C、D、E、F六足球队进行单循环比赛，当比赛到某一天时，统计出A、B、C、D、E、五队已分别比赛了5、4、3、2、1场球，则还没与B队比赛的球队是______　 。

15、甲从A地到B地，去时步行，返回时坐车，共用x小时，若他往返都座车，则全程只需小时，，若他往返都步行，则需____________小时。

16、李志明、张斌、王大为三个同学毕业后选择了不同的职业，三人中只有一个当了记者。一次有人问起他们的职业，李志明说：“我是记者。”张斌说：“我不是记者。”王大为说：“李志明说了假话。” 如果他们三人的话中只有一句是真的， 那么_______是记者。

17、

18、若正整数x，y满足2004x＝15y，则x＋y的最小值是_______________。　　　

三、解答题(每小题10分，共40分)

19、现将连续自然数1至2009按图中的方式排列成一个长方形队列，再用正方形任意框出16个数。

1　　  2　　  3　　  4　　  5　　  6　　  7 　8　　　　　9　　　　　10　　　　 11　　　　 12　　　　 13　　　 14 　 15　　　　 16　　　　 17　　　　 18　　　　 19　　　　 20　　　 21 　 22　　　　 23　　　　 24　　　　 25　　　　 26　　　　 27　　　 28 　 ·　　　　 ·　　　　 ·　　　　 ·　　　　 ·　　　　 ·　　　 · 　 ·　　　　 ·　　　　 ·　　　　 ·　　　　 ·　　　　 ·　　　 · 　 ·　　　　 ·　　　　 ·　　　　 ·　　　　 ·　　　　 ·　　　 · 　 1996　　　1997　　 1998　　 1999　　 2000　　 2001　2002 　 2003　　　2004　　 2005　　 2006　　 2007　　 2008　2009

　　　　　　　　　  　　　　　　　　　　　　　　　　　

 

（1）设任意一个这样的正方形框中的最小数为，请用的代数式表示该框中的16个数，然后填入右表中相应的空格处，并求出这16个数中的最小数和最大数，然后填入右表中相应的空格处，并求出这16个数的和。（用的代数式表示）

（2）在图中，要使一个正方形框出的16个数之和和分别等于832、2000、2008是否可能？若不可能，请说明理由；若可能，请求出该正方形框出的16个数中的最小数和最大数。

20、电子跳蚤落在数轴上的某点K₀，第一步从K₀向左跳1个单位到K₁，第二步由K₁向右跳2个单位到K₂，第三步由K₂向左跳3个单位到K₃，第四步由K₃跳4个单位到K₄，…，按以上规律跳了100步时，电子跳蚤落在数轴上的点K₁₀₀所表示的数恰是20，试求电子跳蚤的初始位置K₀点所表示的数。

21、老师带着两名学生到离学校33千米远的博物馆参观．老师乘一辆摩托车，速度25千米／小时．这辆摩托车后座可带乘一名学生，带人后速度为20千米／小时．学生步行的速度为5千米／小时．请你设计一种方案，使师生三人同时出发后都到达博物馆的时间不超过3小时。

七年级数学竞赛试题答案

1	2	3	4	5	6	7	8	9	10
D	A	A	C	C	C	A	D	B	A

11、6 ;12、-89 ; 13、 0 ，1 ; 14、 E ; 15、  ;16 、张斌;　17、 ; 18、673.

19、答案：1、 n　　　 n+1　　　 n+2　　　n+3

　　　　 n+7　　  n+8　　　 n+9　　  n+10

　　　　 n+14　　 n+15　　  n+16　　 n+17

　　　　 n+21　　 n+22　　  n+23　　 n+24

这16个的和=16n+192=16（n+12）

2、设　　　16（n+12）=832　 n=40　　　∴存在最小为40，最大40+24=64

16（n+12）=2000　 n=113　　 ∴存在最小为113，最大为137，

16（n+2）=2008　  n=125.5， ∴不存在。

20. 答案 设K0点所表示的数为x，则K1，K2，K3，…，K100所表示的数分别为，，，…，.　由题意知：＝20所以x=- 30.

21、答案 解：让一A 同学先步行，老师乘摩托车带B 同学行驶小时后，让B同学步行至博物馆，老师返回接A同学，并带他到博物馆，则有；

　 当时，，，

，，能到，

故，让A同学先行，老师乘摩托车带B同学行驶1.2 小时，也就是24千米后，让B步行至博物馆，老师返回接A 同学，这样，3小时后，三人同时到达博物馆。