三 角 形
(时间:45分钟 满分:100分) 姓名
一、选择题(每小题4分,共24分)
1.图中三角形的个数是( )
![]()
A.8 B.9 C.10 D.11
2.下面四个图形中,线段BE是⊿ABC的高的图是( )
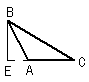
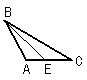
A. B.
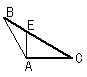
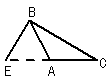
C. D.
3.以下各组线段为边,能组成三角形的是( )
A.1cm,2cm,4cm
B.8cm,6cm,4cm
C.12cm,5cm,6cm
D.2cm,3cm,6cm
4.三角形一个外角小于与它相邻的内角,这个三角形是( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.属于哪一类不能确定
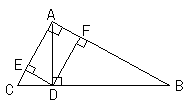
5.如图,在直角三角形ABC中,AC≠AB,AD是斜边上的高,DE⊥AC,DF⊥AB,垂足分别为E、F,则图中与∠C(∠C除外)相等的角的个数是( )
6.下面各角能成为某多边形的内角和的是( )
A.430° B.4343°
C.4320° D.4360°
二、填空题(每空4分,共24分)
7.如图,在⊿ABC中,AD是中线,则⊿ABD的面积 ⊿ACD的面积(填“>”“<”“=”)。
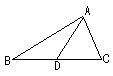
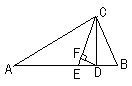
(第7题图) (第8题图)
8.如图,⊿ABC中,∠A = 40°,∠B = 72°,CE平分∠ACB,CD⊥AB于D,DF⊥CE,则∠CDF = 度。
9.一个四边形的四个内角中最多有 个钝角,最多有 个锐角。
10.一个多边形的每一个外角都等于30°,这个多边形的边数是 ,它的内角和是 。
三、想一想(本题7分)
11.有人说,自己的步子大,一步能走三米多,你相信吗?用你学过的数学知识说明理由。
四、试一试(每题10分,共20分)
12.小颖要制作一个三角形木架,现有两根长度为8m和5m的木棒。如果要求第三根木棒的长度是整数,小颖有几种选法?第三根木棒的长度可以是多少?
13.小华从点A出发向前走10m,向右转36°然后继续向前走10m,再向右转36°,他以同样的方法继续走下去,他能回到点A吗?若能,当他走回到点A时共走多少米?若不能,写出理由。
五、算一算(本题15分)
14.⊿ABC中,∠ABC、∠ACB的平分线相交于点O。
(1)若∠ABC = 40°,∠ACB = 50°,则∠BOC = 。
(2)若∠ABC +∠ACB =116°,则∠BOC = 。
(3)若∠A = 76°,则∠BOC = 。
(4)若∠BOC = 120°,则∠A = 。
(5)你能找出∠A与∠BOC 之间的数量关系吗?
六、小设计(本题10分)
15.一块三角形优良品种试验田,现引进四种不同的种子进行对比试验,需要将这块地分成面积相等的四块,请你设计出两种划分方案供选择,画图说明。
附:命题意图及参考答案
(一)命题意图
一、 选择题
1.考查三角形的概念,看能从复杂的图形中分解出基本图形,会采用适当的方式找到这些基本图形。
2.考查三角形高的概念。
3. 考查学生是否掌握了三角形三边关系。
4.考查学生是否掌握三角形外角概念及三角形分类。
5.考查三角形的高及三角形的内角和等于180°,看学生是否能综合运用。
6.考查多边形的内角和公式,了解学生能否利用方程思想方法来解决问题。
二、 填空题
7.考查三角形中线的概念及三角形面积公式。
8.考查三角形的高、角平分线及三角形内角和等于180°。
9.考查学生能否运用四边形的内角和是360°说明有关结论。
10.考查多边形内角和与外角和公式。
三、想一想
11.考查三角形的三边关系,让学生体会数学在生活中的实际运用。
四、试一试
12.考查三角形的三边关系及其在实际中的应用,发展学生的应用意思。
13.考查正多边形的概念的理解,发展学生的抽象思维能力。
五、算一算
14.考查角平分线及三角形内角和公式的综合运用。
六、小设计
通过具体情境的创设,调动学生学习数学的兴趣,考查学生能否采用多种方式解决问题的能力。
(二)参考答案
1.B
2.A
3.B
4.C
5.B
6.C
7. =
8.74°
9.3,3
10.12,1800°
11.不能。如果此人一步能走三米多,由三角形三边的关系得,此人两腿的长大于3米多,这与实际情况不符。所以他一步不能走三米多。
12.小颖有9种选法。第三根木棒的长度可以是4cm,5cm,6cm,7cm,8cm,9cm,10cm,11cm,12cm。
13.小华能回到点A。当他走回到点A时,共走1000m。
14.(1)135°
(2)122°
(3)128°
(4)60°
(5)∠BOC = 90°+ ![]() ∠A
∠A
15.以下是部分答案:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()